應用Excel進行藥物有效期的統計分析及預測

曹悅興，劉新寧，滕學厚

(1.山東大學藥學院，山東 濟南250012;2.濟南利民制藥有限責任公司，山東 濟南250200)

ICH指導原則Q1E附錄B［1］介紹了貨架壽命的評價方法，但對批的合并檢驗等未作詳細說明，筆者利用常用數據處理軟件Excel，通過對穩定性試驗數據進行系統的統計學整理并預測了有效期。

1 穩定性數據的分類

ICH指導原則中需要用到統計學分析的有三種，一為各批的穩定性數據可以合并，即各批次不能拒絕斜率及截距均相同的假設;二為拒絕截距相同的假設，但不能拒絕斜率相同的假設;三為拒絕斜率相同的假設。這三種情況需要分別進行分析。

2 理論分析及實際應用

本內容根據邏輯關系分為兩部分，第一部分為穩定性數據的處理及回歸直線的合并分析，第二部分為合并后根據回歸直線的置信區間以確定有效期。

2.1 第一部分［2～4］通過統計學分析確定穩定性試驗數據并判斷如何合并處理，每一個檢驗均用0.25的顯著性水平來補償由于正式穩定性試驗時樣本量限制所導致的設計上的不足。

2.1.1 本文的思路 穩定性試驗數據中某定量特性y可以看做是時間x(或經函數轉換)的函數，通常假設其是呈線性關系的。在回歸方程中兩個有相關關系的變量x和y的一元線性回歸模型可表示為

①證明各回歸方程有意義，即回歸顯著性檢驗，并在其基礎上進行方差齊性檢驗，若方差齊性檢驗無法通過，則認為各直線存在顯著性差異，不能進行合并統計分析;②證明各方程的斜率相等;③證明各方程的截距相等，確定合并的回歸方程。

2.1.2 具體的理論分析及實際應用

2.1.2.1 回歸顯著性試驗與方差齊性試驗

2.1.2.1.1 理論分析 方差齊性檢驗首先利用Excel的回歸功能，確定各回歸方程具有顯著意義。并計算出SSE1，SSE2，SSE3…;MSE1，MSE2，MSE3…，其意義為:

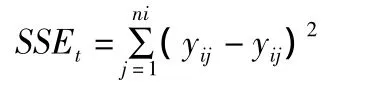
MSE=SSEi/γi，為的無偏估計量。式中γ為自由度，其值為 ni－2(i=1，2，3…k)，ni是建立回歸直線 Li時的樣本容量)(i=1，2，3…)。

由于有k條直線，而F分布僅能證明兩條直線方程誤差項方差相等，因此需進行相應處理，又因為MSEi為的無偏估計量，因此我們可以選擇MSE的最大與最小值，即誤差項差別最大的進行比較，差別大方差相等，差別小自然相等。

判斷標準:

2.1.2.1.2 實際應用 實驗中測得某藥品在穩定性研究長期試驗中標示含量數據如下，該數據作為本文的應用案例(見表1)。

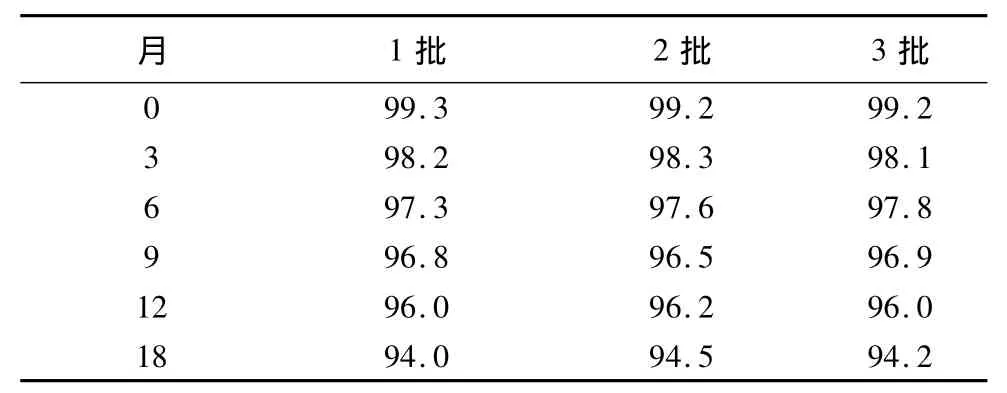
表1 某藥品穩定性研究長期試驗中標示含量數據(%)

利用Excel軟件的回歸功能得結果，見表2。

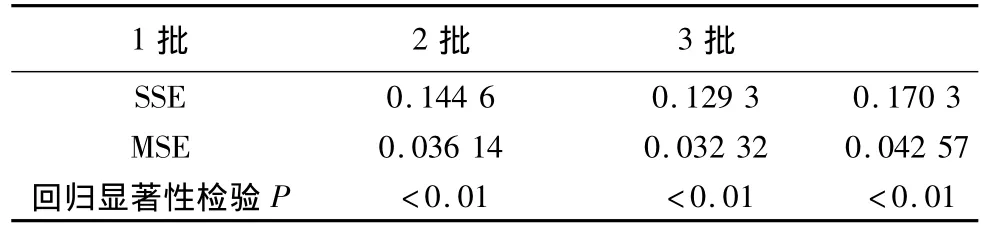
表2 使用Excel軟件的回歸功能所得結果

由回歸顯著性檢驗(F檢驗)可知，檢驗拒絕回歸系數為零的假設，即回歸顯著。

從而可知第3批MSE3最大，第2批MSE2最小，則可得F 值為 MSE3/MSE2=1.317。

利用函數 FINV(p，γi，γj)，求得 F0.25(4，4)=2.064 ＞ F，因此可證明各直線誤差項齊方差。

如果結論不能證明各直線誤差項齊方差，則各直線無統計學意義，可采用ICH指導原則中其他有關規定。

2.1.2.2 等斜率試驗

2.1.2.2.1 等斜率檢驗 基本思想為首先用最小二乘法計算出共同的斜率，假設各直線的斜率相等，利用斜率相等條件下計算得到的總的殘差平方和與不采用斜率相等條件下計算得到的總的殘差平方和的差異來設立F檢驗，根據F值的概率大小來判斷斜率相等的條件是否成立。

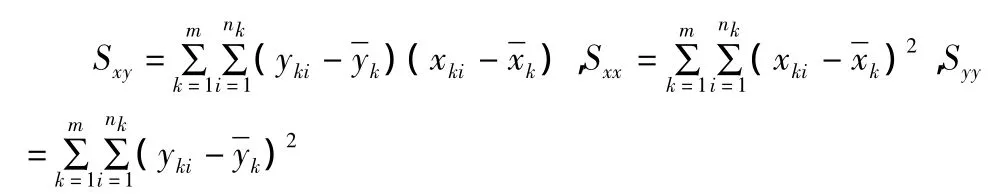
式中m為數據組數，如有3批數據則m值為3，nk為各組數據中對應的數據組數，例如第 i組(xi，yi)(i=1，2，3…ni.)中有 ni個數組;的平均指的是各組數據的相應平均值。

共同斜率β的計算公式:及

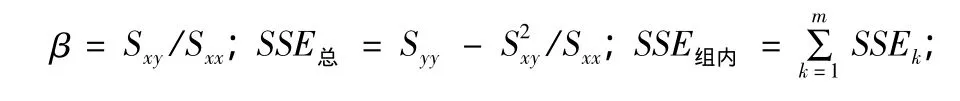
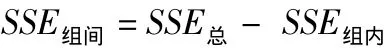
各參數的自由度:SSE組間為m－1;SSE組內為SSE總為

判斷標準:

2.1.2.2.2 回歸顯著性檢驗 基本思想為假設斜率為零的條件下計算得到的回歸平方和與殘差平方和的差異來設立F檢驗，根據F值的概率大小來判斷假設是否成立。

回歸平方和SSR=SST－SSE，即回歸偏差=總偏差－剩余偏差。

SSR自由度為γ1=1，SSE自由度為2);

提出假設:H0:βi=0;H1:βi不全為 0

若 F≥Fα(γ1，γ2)，則拒絕 H0，說明總體回歸系數 β≠0，即回歸是顯著的。

2.1.2.2.3 實際應用 等斜率檢驗:

使用Excel函數 COVAR、DEVSQ求得 Sxy=－170;Sxx=630;Syy=46.38

β=Sxy/Sxx= －0.269 8;SSE總=0.508 7;SSE組內=SSE1+SSE2+SSE3=0.444 1;SSE組間=0.064 51。其中 SSE組間自由度為2，SSE組內自由度為12。

F=(SSE組間/γ組間)/(SSE組內/γ組內)=0.871 4

F0.75(2，12)=0.294 7 ＜ F ＜ F0.25(2，12)=1.560，接受斜率相等的假設。

回歸顯著性檢驗:

SSR=Syy－ SSE=45.87，自由度為1;SSE=0.508 7，自由度為14。

F=(SSR/γ1)/(SSE/γ2)=1262 ＞=8.862，說明總體回歸系數β≠0，即回歸是顯著的。

2.1.2.3 等截距試驗

2.1.2.3.1 理論分析 基本思想為已證明斜率相等成立的基礎上，在假設截距相等條件下計算得到的殘差平方和與僅斜率相等條件下計算得到的殘差平方和差異來設立F檢驗，根據F值的概率大小來判斷假設是否成立。

在斜率、截距均相等的條件下，各組數據可以合并為一組，可計算殘差平方和，其自由度為僅斜率相等的條件下的殘差平方和為SSE總(上面內容已求得)，其自由度為;其差值為SSE總，自由度為 γ3=γ1－γ2=m －1。

判斷標準:

若 F0.75(γ3，γ2)＜ F ＜ F0.25(γ3，γ2)，則接受截距相等的假設，即截距不存在顯著差異;若 F ＞F0.25(γ3，γ2)或 F ＜F0.75(γ3，γ2)，則拒絕截距相等的假設，認為截距存在顯著差異。

2.1.2.3.2 實際應用 等截距檢驗:將所有數據合并為一組，并用 Excel求得 SSE總＇=0.556 4，其自由度為 16;可得SSE總＇－SSE總=0.047 70，其自由度為2。

F0.75(2，14)=0.293 7 ＜ F=0.656 4 ＜ F0.25(2，14)=1.533，說明各組截距相等，數據組可以合并，合并后的方程為y=－0.269 8x+99.16。

2.2 第二部分 根據ICH指導原則中分為三類情況。

2.2.1 不能拒絕斜率及截距均相同的假設的情況 使用Excel預測藥物有效期［5］，原理:根據給定的顯著水平 α，可得到對應于x0的預測值y0的區間估計。

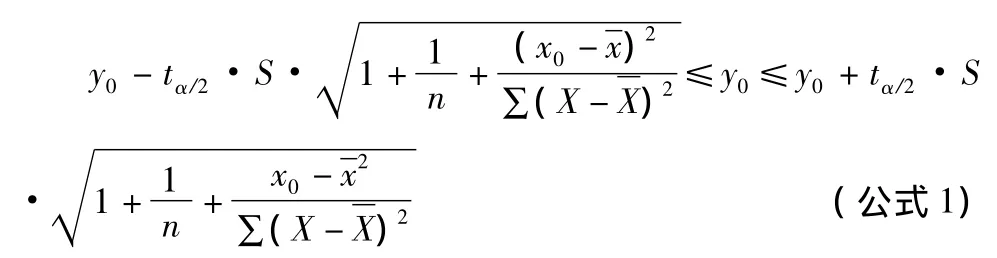
根據各月的含量數據求得對應的 z=tα/2·S·，并求得估計數據y0，及其波動范圍下限y0－Z，上限 y0+Z;分別對各組估計數據(x0，y0)，下限(x0，y0－Z)，上限(x0，y0+Z)作趨勢線，以二次曲線進行回歸，根據需要的限值代入進行計算。

計算時采用平均值單側95%置信限，即雙側顯著水平為0.1。如果為減少趨勢，執行下限;如果為增加趨勢，執行上限(圖1)。

可得

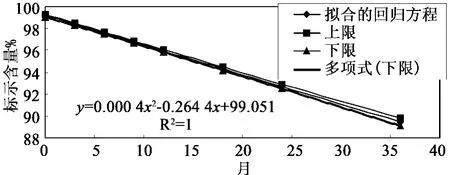
圖1 藥品品有效期估算圖

回歸得曲線方程:y= －0.000 4x2－0.264 4x+99.051，如果限值為標示含量不得低于90.0%，將y=90.0代入，解得x值為32.6月。

2.2.2 拒絕截距相同的假設，但不能拒絕斜率相同的假設的情況 需要做的工作:本文的第一部分，第二部分斜率相同的檢驗及回歸檢驗，截距相同假設被拒絕的檢驗，然后利用合并后的共同斜率，根據公式，分別求得各自的截距a，然后利用上述方法分別預測各自有效期，然后取較短者。

2.2.3 拒絕斜率相同的假設的情況 ICH指導原則要求:求得各批次截距、各個斜率及從全部批次計算得到的平均方差，來估算在穩定性研究中各個批次的再試驗期和貨架期。所有批號中最短的估測值應被選作全部批次的再試驗期或貨架期。

需要做的工作:本文的第一部分，分別求得各自的截距及斜率，第二部分斜率假設被拒絕的檢驗，然后利用全部批次計算得到的平均方差代入公式1中分別計算得各批的上限及下限，其它處理相同。

3 討論

3.1 文中討論了穩定性試驗數據中某定量特性y與時間x呈線性函數關系的處理方法，對于呈非線性函數關系的可以通過適當的轉換使之成為線性函數關系，然后進行相應的處理。

3.2 檢驗順序一定要按σ2、β和α的順序進行，因為后一步的檢驗將用到前一步檢驗的結果，如果有一步檢驗無法通過，則需要通過文中介紹的其他方法進行分析。

3.3 Excel是最常用的數據處理軟件，數據處理簡明、直觀、準確，操作簡便，易于掌握，采用此軟件進行統計分析，便于學習者掌握，理解。

3.4 通過對多批穩定性試驗數據進行系統的統計學整理并預測了有效期，解決了藥品研發過程中的實際問題。

［1］周海鈞.藥品注冊的國際技術要求(中英對照2007質量部分)［M］.北京:人民衛生出版社，2006.

［2］盛驟，謝式千，潘承毅.概率論與數理統計［M］.第4版.北京:高等教育出版社，2008.

［3］莊常陵.兩條回歸直線的比較［J］.高等函授學報(自然科學版)，2005，19(5):38 －40.

［4］王公恕.回歸直線平行性檢驗的一個應用［J］.數理醫藥學雜志，2001，14(6):526 －527.

［5］趙康虎，劉元瑞.利用電子表格Excel 2000預測藥物有效期［J］.中國現代應用藥學，2001;18(6):478－479.