對資本資產定價模型與套利定價模型的比較分析

丁 瑤 （重慶大學，重慶 400044；重慶電子工程職業學院，重慶 401331）

對資本資產定價模型與套利定價模型的比較分析

丁 瑤 （重慶大學，重慶 400044；重慶電子工程職業學院，重慶 401331）

介紹了資本資產定價模型和套利定價模型，分析了兩個模型之間的聯系和不同之處，并提出了兩個模型有待繼續研究和改善的地方。

資本資產定價模型；套利定價模型；異同

1 資本資產定價模型與套利定價模型的簡介

1.1 資本資產定價模型(簡寫為CAPM)

CAPM模型是Sharpe在1964年提出的，用來分析系統風險和非系統風險，用線性關系表達了風險資產的收益與風險的關系，并分析了資產的期望收益率與風險之間的關系。其表達式為：

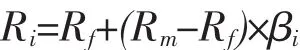
其中，Ri表示第i種資產的期望收益率,Rf表示市場無風險收益率,Rm表示市場證券組合平均風險收益率,(Rm-Rf)表示市場組合的超額收益，市場風險超額收益決定于投資者的風險回避程度。βi表示資產收益變動對市場組合收益變動的敏感度系數。

1.2 套利定價模型(簡寫APT)

APT模型是Ross在1976年首先提出的，也是一個決定資產價格的均衡模型，APT認為風險資產的收益率不但受市場風險的影響，還存在一些共同因素，風險資產的收益率也會隨著這些共同因素的變動而變動。APT模型將CAPM模型從單因素模式擴展成為多因素模式，也更加適應現實經濟生活的復雜情況。多因素模型表達式為：

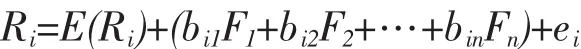
其中，Ri是公司第i種資產的收益率，E(Ri)是第i種資產的期望收益率,Fj表示第j個共同因素對期望值的偏離，bij表示第i種資產對第j共同因素的非預期變化敏感性，比如GDP因素、市場因素、市場利率、股價因素、通貨膨脹，等等。ei是公司特有因素對收益的影響，與共同因素變動無關，是公司特有風險造成的。當只有一個共同因素時，就是單因素模型。

2 資本資產定價模型與套利定價模型的不同之處

2.1 CAMP模型與APT模型的前提假設

CAMP模型與APT模型的基本假設有很多不同，和CAMP模型相比，APT模型的假設條件較為寬松，投資分析不用限定在“單一投資期”；投資者也不需要按無風險利率無限制的借貸；也沒有規定投資者的風險態度，投資者可以持不同的風險態度，而且也不要求投資者構建最優的投資組合。在投資者群體上，APT模型的實用性大大的增加，較小程度地限制了投資者對風險和收益的偏好假設，所以APT模型被認為是一個比CAPM更好的替代模型。

兩者相比較，CAMP模型的假設條件較多，所得出的模型表達式簡單明了；APT模型的假設條件雖然簡單得多，但所得出的模型表達式比較復雜，需要估計參數也更多,其共同因素的篩選比較困難：一方面，假設中風險投資收益率會受到很多因素的影響，但不能驗證具體受到了哪些因素的影響，因此，在選擇具體的因素作為風險投資收益率的共同因素進行回歸分析時，會出現偽回歸問題；另一方面，在解釋風險投資收益率時，即使知道了某些因素會對某一種風險投資產生影響，但這些因素之間可能存在相關或共線關系，以這些因素作為自變量則可能會導致系數的不穩定性。

2.2 CAMP模型與APT模型的可實踐性

作為當代金融領域的經典模型，CAMP模型雖然能很好地反映風險資產的期望收益率與風險之間的關系，為投資者風險投資進行指導。但是，CAMP模型的實用性卻不大，比如對于某種證券進行風險收益分析，需要求出n個方差、n個均值、以及n(n-2)/2個相關系數。以n=1000為例，總共需要收集個501 500個數據，這對實際操作來說是非常困難的。而很多大型券商需要進行動態跟蹤的證券往往比1 000還要多，因此，CAMP模型的可行性不強。

如果用APT單因素模型來進行分析，需要n個市場風險系數，n個期望收益值，n個個別因素方差，1個市場組合方差，只需估計3n+1個數據，同樣1000個證券，只需估計3 010個數據。因此APT模型比CAMP模型的更具有可應用性。

2.3 CAMP模型與APT模型對風險的解釋

在CAMP模型中，風險資產的風險只能用該資產收益變動對市場組合收益變動的敏感度系數β來解釋，并且僅用市場風險代表系統性風險去分析系統性風險與風險資產收益率的對應關系，而沒有進一步說明系統性風險的具體引發因素。故CAMP模型可以告訴投資者風險的大小，卻無法說明風險從什么地方來。而APT模型里風險資產的風險是由多個因素共同解釋的，因此它除了能告訴投資者風險的大小，還能說明風險的來源以及風險的影響有多大。

2.4 CAMP模型與APT模型中市場建立均衡的方式

CAPM模型的均衡是一種絕對的靜態的均衡。均衡市場被視為一個靜態市場，CAPM模型的均衡的實現要假定所有投資者都會按Harry M.Markowitz的投資組合理論持有最優投資組合。該最優投資組合都必須是由無風險資產和市場組合而成。且投資者都為理性投資者，對每種風險資產的收益和風險的預期相同，在選擇投資或投資組合的過程中，都會放棄低收益高風險而選擇高收益低風險的投資項目。

APT模型的均衡是一種相對的動態的均衡。均衡市場被它視為是一個在“失衡”與“均衡”之間不斷轉化的動態市場。APT模型的均衡是在投資者的套利行為中實現的，部分理性投資者用構造的套利組合，賣出收益率被高估的風險資產的同時買入收益率被低估的風險資產，這樣一來，高估的風險資產的價格回落，低估的風險資產的價格被拉升，當達到一個新的平衡點時，套利活動終止，從而促使市場恢復到均衡狀態。因此，APT模型的均衡是表現為一種無套利的暫時穩定狀態，這一均衡狀態允許投資者為各種類型，允許投資者有不一樣的投資觀點，允許投資者持有多元化的各自偏好的投資組合，并通過套利行為使自己所持有的組合獲得最大的收益。

3 資本資產定價模型與套利定價模型的相同之處

隨著資本市場的發展，投資者和籌資者對量化風險管理風險的需求也越來越大。雖然APT模型比CAMP模型晚兩年提出，但它們都是為了解決相同的問題——如何給風險合理定價。兩種模型都假定了資本市場上不存在交易成本或交易稅，即使存在對所有的投資者也都是相同的；兩種模型都將存在的風險劃分為系統風險和非系統風險，即市場風險和公司自身的風險；都認為投資者可以通過多元化組合和合理優化投資結構，能大部分甚至完全消除公司自身的風險。因此，在計算預期收益時，兩種模型都認為資本市場不會因投資者承擔了這部分風險而給予補償，最后都沒有把自身風險計算在內。所以，從某種角度我們可以認為CAMP模型是APT模型在更嚴格假設條件下 (只存在一個風險因子條件)的特例。

模型中的參數估計不夠穩健。CAPM模型最關鍵的是估計β值，由于值是預期β值，無法確定投資者的預測值是多少，因此，我們常常用歷史數據估計出過去一段樣本期內的β值，把它作為預測值使用。 APT模型在實際應用中最重要的是確定模型的影響因素，采用得最多的是因子分析法，先確定該具體投資組合的影響因素以及APT模型的具體形式，再通過歷史數據的回歸分析確定各個影響因素的敏感度，其實質是最小二乘估計。從這兩種模型的實際應用方式可以看出，它們都有一個相同的缺陷——用歷史值代替預測值，由此會帶來一定的偏差，從而影響了模型發揮預測功能。

4 結論

本文介紹了資本資產定價模型和套利定價模型，雖然它們都存在一些不足，但其在理論上和實際運用中的地位還是不可替代的。CAPM模型的優點是其標準化、簡單化，且不單適用于證券市場，對評估不動產等同樣適用。APT模型是復雜化、多元化了的CAPM，它適用于任何資產組合的集合，并且不用限定在單一投資期，在可實踐性和對風險的解釋方面也表現更好。因此，APT模型既是對CAPM模型的一種肯定,也是一種修正和補充。不過，這兩種模型都還存在有繼續發展和完善的地方。比如，在對投資者之間競爭機制的描述上還有欠缺，建立描述資產價格變動趨勢的動態方程方面還有待改進，解釋能力也比較有限。另外，在模型的參數估計方面，原始數據常常具有很多問題不能滿足條件，即便因素的選取和假設條件的設置非常恰當，也很可能得不到好的結果，因此這也對模型中參數估計以及參數估計的穩健性提出了更高的要求。

[1]Sharpe.W.Captial asset prices：a theory of market equilibrium under conditions of risk [J].Journal of Finance，1964，19：425-442

[2]Ross S A.The arbitrage theory of capital asset pricing [J].Journal of Economic Theory，1976（13）：341-360

[3]楊虎，程娟.基于套利定價理論的多因素定價模型的實證研究[J].數理統計與管理，2005（24）.

[4]楊虎，程娟.基于套利定價理論的多因素定價模型的實證研究[J].數理統計與管理，2005（7）：282-285.

[5]陳志芳.資本資產定價理論模型與套利定價模型比較分析[J].昆明理工大學學報，2004，4(1)：52-54.

[6]陳燕.資本資產定價模世與套利定價模型的比較研究[J].商場現代化，2010（36）：70-71.

Comparison between the Capital Asset Pricing Model and Arbitrage Pricing Model

Ding Yao
(Chongqing University,Chongqing 400044;Chongqing College of Electronic Engineering,Chongqing 401331,China)

This paper discusses the capital asset pricing model and the arbitrage pricing model,analyzes the similarities and differences between them,and puts forward some areas of two models which should continue to study and be improved.

capital asset pricing model;arbitrage pricing model;similarities and differences

F73

A

1674－5787（2012）02－0042－03

2012-02-25

丁瑤，女，重慶大學碩士研究生在讀，重慶電子工程職業學院，講師。

責任編輯 王榮輝