行列式幾何化的教學研究

陳志彬，張愛平，李 強

(湖南工業大學理學院應用數學系，湖南株洲412000)

行列式幾何化的教學研究

陳志彬，張愛平，李 強

(湖南工業大學理學院應用數學系，湖南株洲412000)

基于向量內積與外積的幾何意義，將行列式用向量的這2種運算形式表示，揭示空間中由向量構成的平行四邊形的面積或平行多面體的體積與行列式之值的關系，將行列式幾何化，豐富直觀教學內容，探索行列式教學的新途徑。

行列式;幾何化;超平面;超平行多面體

行列式是線性代數中的一個重要內容，是教學中的難點和重點，線性代數中的許多概念都與行列式密切相關，掌握好行列式是學好線性代數的關鍵。目前，國內編寫的線性代數教材把行列式的內容都放在第一章，多數教材是以消元法求解二元或三元線性方程組引入行列式概念的，把線性方程組的解化歸為統一形式，將求解問題轉化為單純的計算行列式的問題，向學生演示引入行列式概念的背景知識，表明線性方程組與行列式存在某種代數運算關系。然而，這些卻未能將幾何與代數有機結合起來，向學生呈現出蘊含的幾何背景知識，讓學生從幾何的角度更好地理解線性方程組的解;特別是關于行列式的性質，多數教材僅以代數的各種運算關系給出介紹與證明，利用定義證明行列式性質的純代數方法常常令學生感到抽象;在行列式教學中，多數教師僅重視計算行列式的運算技巧而忽視行列式的幾何解釋，讓學生難以接受。因此，針對行列式教學中存在的這些不足，本文用類比法將行列式與向量相結合，在歐氏空間中通過引入正交坐標系，用向量的內積和外積的運算形式表示行列式的值，或用投影降維的方法探索行列式與多個平行多面體的關系，將行列式幾何化，從而改革關于行列式傳統的教學方法和內容，促進學生的直觀思維，化代數抽象問題為幾何的具體問題。

一 向量的內積、外積與行列式幾何化的關系

向量是一個既有大小又有方向的量，是一個幾何概念的量。由于引入笛卡爾坐標系，把向量表示成關于坐標的有序數組，實現了向量的幾何運算向代數運算的轉化。向量的加法、減法、內積和外積4種運算成為超越坐標幾何的有力工具，使得坐標系中不能進行運算的點具有了按向量運算的功能。因此，利用向量，巧妙地解決了直線與直線的垂直或平行關系、空間中線面或面面之間的位置關系等幾何問題，實現了數形的完美結合。行列式在本文中被作為關于向量的一張表，其定義看成是表上的一種算法，行列式的值與表中向量組成的幾何圖形相對應，按照對行列式幾何化的這一思路，首先在二維和三維空間中討論行列式的幾何化問題，然后將其推廣到高維空間，最后獲得行列式統一的幾何化的結論。

便于后面討論，首先介紹向量的內積和外積的概念及幾何解釋。在三維空間中，設x、y和z軸的單位正向量分別用 i﹑ j﹑ k 表示，已知向量 a=(ax，ay，az)，b=(bx，by，bz)，根據向量的內積運算定義:

向量的外積運算定義如下:

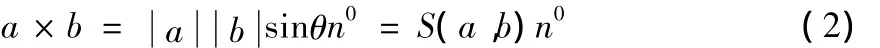
其中θ(0≤θ≤π)為向量a到b所成的角，S(a，b)表示a，b 2個向量張成的平行四邊形的面積，n0是依右手法則垂直于由向量a到b所張成的平面的單位法向量。式(2)的幾何解釋是a×b表示一個新的向量，大小等于向量a﹑b張成的平行四邊形的面積S(a，b)，方向垂直于a到b所張成的二維平面。由此可知，在坐標運算中外積的概念只適合于三維及三維以上的向量空間，2個向量的外積等于他們所張成的平行四邊形的有向面積S(a，b)n0，在三維向量空間中，利用(2)式，可得x、y和z軸的單位正向量i﹑j﹑ k的外積運算式:i× j=k，j× k=i，k× i=j，以及向量a與b的外積運算式:

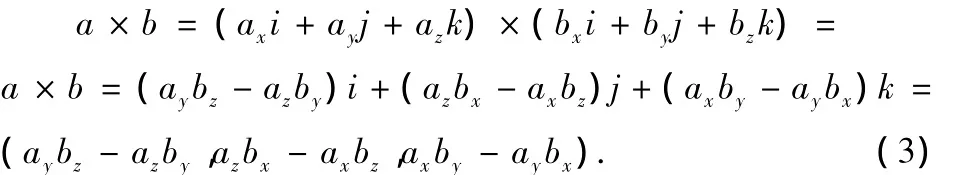
利用二階、三階行列式又可把(3)式改寫成關于x、y和z軸上三個向量的線性組合形式

在(2)式中，如果令法向量n0與x、y和z軸所成的角分別記為 θ，β，γ，則單位法向量 n0=(cosθ，cosβ，cosγ)，其中jcosβ+kcosγ)，由此可得:向量a×b的坐標則具有如下的幾何解釋:

(ⅰ)當Ax＞0(Ax＜0)時，表明cosθ＞0(cosθ＜0)即單位法向量n0指向x軸的正向(x軸的反方向)，Ax為向量a﹑b張成的平行四邊形在yoz坐標平面上的有向面積投影。

(ⅱ)當Ay＞0(Ay＜0)時，表明cosβ＞0(cosβ＜0)單位法向量n0指向y軸的正向(y軸的反方向)，Ay為向量a﹑b張成的平行四邊形在zox坐標平面上的有向面積投影。

(ⅲ)當Az＞0(Az＜0)時，表明cosγ ＞0(cosγ ＜0)單位法向量n0指向z軸的正向(z軸的反方向)，Az為向量a﹑b構成的平行四邊形在xoy坐標平面上的有向面積投影。

二 二維和三維空間中行列式的幾何化

下面將向量張成的平行四邊形的有向面積或平行多面體的有向體積，用降維的方法向坐標面投影，討論二階行列式和三階行列式幾何化的問題。

可從向量的三維空間和二維空間2個角度對二階行列式做出如下幾何化解釋:

ⅰ)在三維空間中，取向量的第三個坐標為零，即向量a1=(a11，a12，0)，a2=(a21，a22，0)，向量 a1與 a2張成的平行四邊形落在xoy坐標面上，通過增加向量的維數，由坐標面上的平行四邊形看成是由三維空間中的向量a1與a2張成的平行四邊形在xoy坐標面上的投影，這個平行四邊形的有向面積為S(a1，a2)k，二階行列式的值為S(a1，a2)，如果S(a1，a2)＞0，則表明按右手法則選擇以向量a1的方向為始邊，依逆時針轉過一個θ(0≤θ≤π)角達到向量a2，右手拇指的指向與z軸的正方向一致;如果S(a1，a2)＜0，則按右手法則選擇以向量a1的方向為始邊，依順時針轉過一個θ(0≤θ≤π)角達到向量a2，右手拇指的指向與z軸的反方向一致;如果S(a1，a2)=0，則向量a1與向量a2共線。

ⅱ)在二維空間中，取向量 a1=(a11，a12)，a2=(a21，a22)，引入記號，其中向量ai(i=1，2)在x軸上的坐標記為 ai1(i=1，2)，向量ai(i=1，2)在y軸上的坐標為ai2(i=1，2)，行列式的值表成了行列式的2個行向量在x軸上的坐標與在y軸上的坐標之間乘積的代數和，而數a11a22與 －a12a21分別對應2個矩形的有向面積。對于第一項a11a22，如果a11a22＞0，則表明以向量)為始邊，依逆時針轉過一個θ(0≤θ≤π)角達到向量)，如果a11a22＜0，則表明以向量為始邊，依順時針轉過一個θ(0≤θ≤π)角達到向量;對于第二項 －a12a21，如果－a12a21＞0，則表明以向量為始邊，依逆時針轉過一個θ(0≤θ≤π)角達到向量，如果－a12a21＜0，則表明以向量為始邊，依順時針轉過一個θ(0≤θ≤π)角達到向量

ⅰ)在三維空間中，用向量的外積運算對行列式的性質解釋如下:

令三維向量 a1=(a11，a12，0)，a2=(a21，a22，0)，a3=(a21+ka11，a22+ka12，0)，則 a1× a3=a1× (a2+ka1)=

這表明向量a1與向量a3張成的平行四邊形的有向面積與向量a1與向量a2張成的平行四邊形的有向面積相等。

ⅱ)在二維空間中，可作如下幾何解釋:

二維向量 a1=(a11，a12)與 a3=(a21+ka11，a22+ka12)張成平行四邊形是由向量a1=(a11，a12)與a2=(a21，a22)張成平行四邊形在保持同底同高的情況下發生切變所得，這2個平行四邊形的面積相等，法向量的方向不變。

利用(1)(2)中的方法，對二階行列式的其它性質同樣可以做出類似的幾何解釋，故略去．下面探討三階行列式幾何化的問題:

問題3:三階行列式

ⅰ)設三維向量 a(1)=(a11，a12，a13)，a(2)=(a21，a22，a23)，a(3)=(a31，a32，a33)，則有代數等式 (a(2)× a(3))·

或者有等式 (a(2)× a(3))·a(1)=S(a(2)，a(3))［a11cosθ+a12cosβ+a13cosγ］，即三階行列式與三個向量間的混合積的的運算相聯系，(a(2)×a(3))·a(1)對應著一個幾何圖形，表示以3個向量a(1)、a(2)和a(3)為棱長所張成的平行六面體的有向體積。基于代數式S(a(2)，a(3))n0·a(1)分2種情形解釋如下:

第一種情形:外積a(2)×a(3)=S(a(2)，a(3))n0表示以坐標原點為始點的2個向量a(2)到a(3)所張成的平行四邊形的有向面積，單位法向量n0的指向由向量a(2)旋轉到向量a(3)的方向確定，如果平行四邊形是以向量a(2)為始邊依順時針轉過一個θ(0≤θ≤π)角到向量a(3)張成的，則單位法向量n0指向平行四邊形的下側，如果向量a(1)的方向與單位法向量n0垂直，則向量a(1)與向量a(2)，a(3)共面，三階行列式的值S(a(2)，a(3))n0·a(1)=0;如果平行四邊形是以向量a(2)為始邊依逆時針轉過一個θ(0≤θ≤π)角到向量a(3)張成的，則法向量n0指向平行四邊形的上側;n0?a(1)為向量a(1)在單位法向量n0上的投影，如果向量a(1)的方向與單位法向量n0同側，則三階行列式的值S(a(2)，a(3))n0·a(1)為正，其值等于這3個向量所張成的平行六面體的體積，如果向量a(1)的方向與單位法向量n0異側，則三階行列式的值S(a(2)，a(3))n0·a(1)為負，等于這3個向量所張成的平行六面體的體積的相反數。

第 二 種 情 形:由 n0· a(1)=[a11cosθ+a12cosβ +a13cos γ ]得三階行列式等于向量a(1)的3個坐標分別乘以一個相應的二階行列式的代數和，代數和式中的每個部分都對應著一個特定的小平行六面體的有向體積，其中，它表示a(2)到a(3)所張成的平行四邊形的有向面積在坐標平面yoz上的有向投影S(a(2)，a(3))cosθ乘以向量a(1)在x軸上的坐標a11，同理第二部分和第三部分分別表示a(2)到a(3)所張成的平行四邊形的有向面積在坐標平面zox上的有向投影面積乘以向量a(1)在y軸上的坐標a12，在坐標平面xoy上的有向投影面積乘以向量a(1)在z軸上的坐標a13．因此，由3個向量在三維空間中所張成的平行六面體的有向體積等于底在坐標平面上高在坐標軸上的3個小的平行六面體的有向體積之和。

問題4:三階行列式另一種代數形式

a13a22a31－a11a23a32－a12a21a33的幾何化問題。

在問題3中將二階行列式展開可得到上面三階行列式的另一種代數形式，等式中共有六項，每一項由來自3個向量中的不同坐標的3個數相乘，其中有三項的符號為正，其余項的符號為負，對應著將原三階行列式分解成如下的由坐標向量構成的六個三階行列式的代數和，即由3個向量a(1)、a(2)和a(3)的坐標向量作混合積得到:

增加向量的維數，類似于將幾何圖形由三維投影到二維解釋二階行列式的方法，同理在四維空間中亦可解釋三階行列式的幾何化問題。首先建立四維正交坐標系，設正交單位坐標向量 e1=(1，0，0，0)，e2=(0，1，0，0)，e3=(0，0，1，0)e4=(0，0，0，1)，其中任意一個向量由其余3 個向量通過下列形式定義的外積運算得到:

用增加向量維數的方法，再將原3個三維向量a(1)、a(2)和a(3)中的坐標增加一個，增加的第四個坐標都為0，不妨得到相應的3個四維向量仍記為a(1)、a(2)和a(3)，這三個四維向量的外積a(1)×a(2)×a(3)是一個新的向量，通過計算得等式:，因此，三階行列式是由3個四維向量a(1)、a(2)和a(3)所張成的超平行多邊形的有向面積，也可以解釋為在四維空間中由3個向量張成的有向超平行多邊形在三維空間上的有向投影。如果三階行列式的值為正，則有向超平行多邊形的方向指向坐標軸e4的反方向，如果三階行列式的值為負，則有向超平行多邊形的方向與坐標軸e4的方向一致。

在上面的討論中得到:行列式對應著平行四邊形的有向面積或平行多面體的有向體積，并且可以分解成由坐標向量構成的若干個簡單行列式的代數和，即二階行列式的有向面積等于2個小長方形的有向面積之和，三階行列式的有向體積等于6個小長方體的有向體積之和，而決定每一個面積塊或體積塊的符號(方向)與乘積項中元素的排列順序有關;若將向量的維數增加一維，則低一維空間中的有向平行多面體可看成高一維空間中的有向超平行多邊形。

三 n維空間中n階行列式的幾何化

根據人的思維具有流暢性的特性，三階行列式能用2個三維向量的外積再與一個向量的內積得到，即向量的混合積(a(2)×a(3))·a(1)表示，學生自然會提出一個問題:一個n階行列式用n維向量有類似的表示嗎?在一般的線性代數教材中都回避了這個問題，使得學生對行列式具有的共性缺乏認識，產生疑惑。實質上n階行列式仍然可以用n－1個n維向量的外積再與一個向量的內積得到，將它化歸為向量運算的一個統一問題。下面引入n維正交坐標系，利用向量的外積與內積運算揭示n維向量與n階行列式的關系。

在n維歐氏空間中，單位正交坐標向量記為

其中任意一個坐標向量用其余的n－1個坐標向量的外積定義如下:

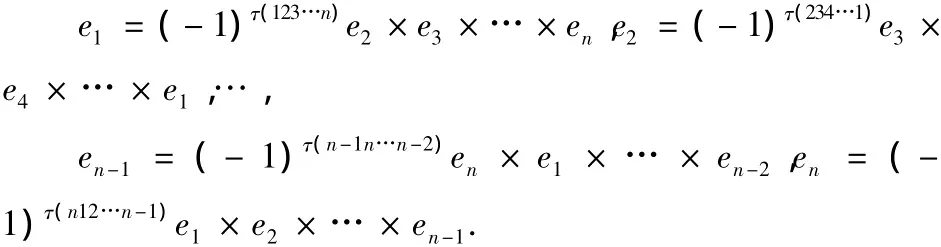
τ(i1i2…in)表示i1i2…in排列的逆序數。

根據向量的運算，任意一個n維向量可表為坐標向量的代數和，于是用坐標向量表成的n－1個n維向量的外積a(2)×a(3)×…×a(n)在以上n－1個坐標向量定義了外積的前提下則是有意義的，它仍是一個n維向量，其向量的長等于這n－1個n維向量張成的超平行多邊形的面積S(a(2)，a(3)，…，a(n))，而外積等于超平行多邊形的面積S(a(2)，a(3)，…，a(n))乘以超平行多邊形的單位法向量n0，通過簡單計算，用一個n階行列式表示如下:

因此，對n－1個n維向量進行外積運算后再與一個n維向量進行內積運算易得到一個數值，故略去計算過程，這個數值對應著一個n階行列式:

上式可作如下幾何解釋:它表示以有向超平行多邊形S(a(2)，a(3)，…，a(n))n0為底，向量 a(1)的長為棱構成的有向超平行多面體的體積。如果n階行列式的值為正，則表明向量a(1)的方向與超平行多邊形的方向同側:如果n階行列式的值為負，則表明向量a(1)的方向與超平行多邊形的方向異側:如果n階行列式的值為0，則表明向量a(1)與超平行多邊形共面。

四 應用舉例

將行列式幾何化的思想應用到幾何中，能巧妙的把向量與平面或多面體結合起來，對獲得的結果賦以新的幾何解釋，下面以幾何中常見的幾個問題為例，對這些簡潔的結論用行列式的幾何解釋說明，旨在拋磚引玉。

解:這個問題若用常規方法，通過求平行四邊形的底和高來求其面積，則顯得繁瑣;若是依照三維空間中兩個向量外積的幾何解釋來求，則是一種簡單的運算，即由下式得

例2．用行列式表示過平面上已知兩點 A(x1，y1)，B(x2，y2)的直線方程．

解:在過 A、B 2點的直線上任取一點 C(x，y)，則A、B、C 三點共線當且僅當(其中λ為常量)成立．由于對二維向量不能進行外積運算，因此，用增加向量的維數方法，將 A、B、C 的坐標擴展到三維即為 A'(x1，y1，1)，B'(x2，y2，1)，C'(x，y，1)且同樣滿足共線的條件則這3個向量張成的幾何圖形是共面的，相當于3個向量張成的平行多面體被壓縮成一個平面，其體積等于零。于是有直線的行列式形式．實質上學生由直線的兩點式很容易得到直線方程，在高中就已經學習過，但是，以此為例能較好地讓學生領會直線方程與行列式和一個幾何圖形的變化關系。

用同樣的方法可推得:過空間中不共線的三點A(x1，y1，z1)，B(x2，y2，z2)，C(x3，y3，z3)的平面方程，其行列式形

類似例2的解釋作同樣的處理，即在A、B、C所在的平面上任取一點 D(x，y，z)，對 A、B、C、D 增加第 4 個坐標且都為1，則得到 4 個四維坐標的點，相應記為 A'，B'，C'，D'由點A、B、C、D共面，推得四維向量3個四維向量所張成的超平行多邊形共面，相當于4個四維向量張成的超平行多面體被壓縮成一個平面，故其體積等于零。

總之，將行列式幾何化引入教學，這能更好地讓學生領會到行列式的應用，有利于學生在后續學習向量的線性相關性和線性變換等知識時，自覺地從幾何的角度思考問題，較好地理解線性代數中諸多抽象的概念。

［1］周 勇，朱 礫．線性代數［M］．上海:復旦大學出版社，2010．

［2］陳志杰．高等代數與幾何［M］．北京:高等教育出版社，2008．

［3］謝 琳，張 靜．從幾何直觀理解行列式與Cramer法則［J］．高等數學研究，2009，12(1):61 －62．

［4］李尚志．從問題出發引入線性代數概念［J］．高等數學研究，2006(6):15－17．

O1512

A

1674－5884(2012)04－0090－05

2012－03－10

湖南省教育科學研究項目(10C0656);湖南工業大學教學改革項目(09E65)

陳志彬(1965－)，男，湖南邵陽人，副教授，碩士，主要從事泛函微分方程研究。

(責任編校 晏小敏)