Logistic回歸模型及其在對(duì)陶瓷坯體性能與組成之間關(guān)系建模中的應(yīng)用＊

高力明 洪日輝 李朝有 劉蓓瑛

（1陜西科技大學(xué) 西安 710021）（2廣西三環(huán)企業(yè)集團(tuán)股份有限公司 廣西 北流 537400）

Logistic回歸模型及其在對(duì)陶瓷坯體性能與組成之間關(guān)系建模中的應(yīng)用＊

高力明1洪日輝2李朝有2劉蓓瑛2

（1陜西科技大學(xué) 西安 710021）（2廣西三環(huán)企業(yè)集團(tuán)股份有限公司 廣西 北流 537400）

陶瓷坯體的性能的測(cè)定結(jié)果往往是以合格與否來表示的。對(duì)于這類只有2種取值的二分類定性變量，當(dāng)以它們作為因變量去建立性能與組成之間關(guān)系的數(shù)學(xué)模型時(shí)，采用通常的最小二乘（OLS）回歸方法存在許多問題。為此，我們引入了Logistic回歸模型。筆者詳細(xì)地介紹了Logistic回歸模型，并給出了在陶瓷磚抗熱震性建模中的成功應(yīng)用示例，以供材料科學(xué)與工程領(lǐng)域的工作者參考與使用。

陶瓷 坯體性能 建模 Logistic回歸模型

前言

材料工作者總是對(duì)材料的性能在某一組成區(qū)域中的分布及變化趨勢(shì)感興趣，并希望能借此找出滿足預(yù)定材料的性能組成及適合的工藝條件。近年來，依照“回歸的試驗(yàn)設(shè)計(jì)”的近、現(xiàn)代數(shù)理統(tǒng)計(jì)理論，并借助于計(jì)算機(jī)技術(shù)，人們?cè)谶@方面的應(yīng)用研究已經(jīng)取得了很大進(jìn)展［1］。并且已形成了一些程式化的，成熟的技術(shù)路線，且已得到推廣使用，取得了良好的效果［2～3］。

關(guān)鍵的一步是建模。即利用試驗(yàn)的測(cè)試結(jié)果，對(duì)性能與組成之間的關(guān)系建立數(shù)學(xué)模型。建模一般可采用通常的最小二乘（OLS，Ordinary Least Square）回歸方法。OLS回歸方法簡(jiǎn)單規(guī)范，有良好的數(shù)理統(tǒng)計(jì)品質(zhì)，其結(jié)果便于做工藝詮釋，而且又有許多成熟的算法及軟件可供調(diào)用。因此，OLS回歸方法已得到廣泛的應(yīng)用，幾乎成為標(biāo)準(zhǔn)的統(tǒng)計(jì)分析工具。但OLS回歸方法的使用是有前提條件的，它通常要求因變量是間隔尺度（又稱“測(cè)度”）變量，也就是平常所說的“連續(xù)變量”；它還要求自變量之間不能完全相關(guān)，這是OLS回歸方法能夠求解的條件。另外，它還有一些關(guān)于誤差項(xiàng)的假設(shè)條件。因此，若將OLS回歸方法用于有序（次序）尺度或名義尺度的因變量問題的求解，由于嚴(yán)重地違反了上述的基本假設(shè)和前提條件，將出現(xiàn)許多問題。諸如，會(huì)導(dǎo)致回歸估計(jì)的推斷存在嚴(yán)重的誤差，以致無論是進(jìn)行假設(shè)檢驗(yàn)，或是計(jì)算置信區(qū)間，均使其失去合理性。也就是說，所得到的結(jié)果將是不可靠和不可信的，最終導(dǎo)致無法作出合理而有價(jià)值的工藝詮釋。

在對(duì)一些陶瓷制品的性能進(jìn)行測(cè)定與表征時(shí)，就有不少這種情況出現(xiàn)。例如，陶瓷磚的抗熱震性、抗凍性，以及日用陶瓷制品的熱穩(wěn)定性等。依照相應(yīng)的測(cè)定標(biāo)準(zhǔn)進(jìn)行測(cè)試，得到的結(jié)果就只分“合格”與“不合格”2類［4～6］。當(dāng)我們?cè)噲D利用這些測(cè)試數(shù)據(jù)去建模時(shí)，就會(huì)遇到違反OLS回歸方法的基本假設(shè)和前提條件的尷尬情況。這就需要尋找另外的解決途徑與方法。

為此，我們擬引入Logistic回歸模型及方法。該模型是基于Logistic函數(shù)（又稱“增長(zhǎng)曲線”），此函數(shù)形式是由比利時(shí)學(xué)者P·F·Verhulst于1838年提出的。經(jīng)過多年的沉寂，直到20世紀(jì)20年代才在生物學(xué)研究中得到實(shí)際應(yīng)用。之后，在人口估計(jì)和預(yù)測(cè)、經(jīng)濟(jì)學(xué)等多個(gè)領(lǐng)域中有了廣泛的應(yīng)用，重新受到世人的關(guān)注。我們也曾在企業(yè)營銷活動(dòng)的研究中有過應(yīng)用［7］。借助于Logistic函數(shù)和概率論，將二分類的定性變量變換成Logistic曲線上的“連續(xù)變量”，從而使之又可以按照OLS回歸方法對(duì)其進(jìn)行處理，并對(duì)其結(jié)果作出合理的解釋。這就是Logistic回歸方法的思路和做法。

我們將對(duì)這種特殊的回歸模型及方法做比較詳盡的介紹，并且給出了在陶瓷磚抗熱震性建模中的應(yīng)用示例。從結(jié)果可以得出，Logistic回歸方法對(duì)于二分類定性變量作為因變量時(shí)的建模是有效的、適用的。這一新的、特殊的回歸模型及方法，進(jìn)一步拓寬了多元統(tǒng)計(jì)分析在材料科學(xué)與工程領(lǐng)域中的應(yīng)用范圍，可供材料工作者在研究工作和開發(fā)新產(chǎn)品時(shí)參考與使用。

1 Logistic回歸模型及方法

在配方問題中，為建立性能與組成之間關(guān)系的模型，所采用的廣義線性回歸方程的一般形式為：

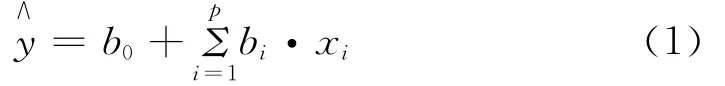
xi——自變量，一般為3大組成或元配料的各種成分?jǐn)?shù)據(jù)及它們的高次項(xiàng)、交互項(xiàng)；

p ——自變量個(gè)數(shù)，即i＝1，2，3，…，p；

b0，bi——分別為常數(shù)項(xiàng)及各自變量項(xiàng)的回歸系數(shù)。

在材料科學(xué)與工程領(lǐng)域中，針對(duì)配方問題，因?yàn)橛谢炝蠗l件的約束限制，而更由于經(jīng)常采用不完全多項(xiàng)式的廣義線性形式，其試驗(yàn)方案多采用單純形格子設(shè)計(jì)。

如前所述，對(duì)于性能測(cè)試值是間隔尺度的連續(xù)變量時(shí)，模型即式（1）的回歸系數(shù)可以用OLS回歸方法解出，并正常地進(jìn)行各種檢驗(yàn)和估計(jì)，但性能測(cè)試值若是二分類定性變量，就不能采用OLS回歸方法。為此，我們需要引入新的模型及方法。Logistic回歸的模型及方法可以較好地解決這一問題。

在Logistic回歸模型中，首先要對(duì)因變量進(jìn)行變換。定義一個(gè)新的因變量Z，并規(guī)定正變換為：

則很容易地推導(dǎo)出其反變換為：

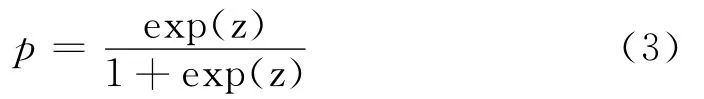
式（2）和式（3）中，p為原來的因變量得概率，0≤p≤1。

我們可以把性能的合格與否作為“事件”，并把p理解為事件“出現(xiàn)”的概率，那么（1－p）就是“不出現(xiàn)”（即“不合格”）的概率。比率p／（1－p）則是“發(fā)生比”。換句話說，新定義的因變量Z就是“發(fā)生比”的（自然）對(duì)數(shù)。此時(shí)，因變量Z已經(jīng)變成一個(gè)連續(xù)變量。它與出現(xiàn)概率p之間的依存關(guān)系可以用表1和圖1表示。由圖1和表1可知，Z可以在（－∞，∞）之間任意取值，而且在進(jìn)行反變換時(shí)，可以保證使p落在閉區(qū)間［0，1］之中，使其概率均有意義。

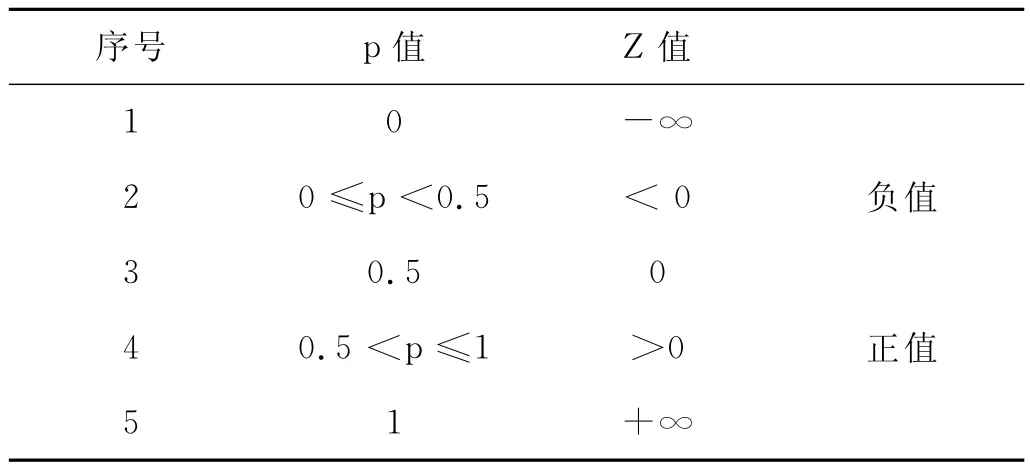
表1 Logistic函數(shù)的若干性狀

如果僅用新的因變量Z取代原來的回歸方程式（1）左部的因變量y，而自變量群，即右部維持不變，就變成Logistic回歸模型。這時(shí)的回歸方程已經(jīng)滿足OLS回歸方法的基本假設(shè)和前提條件，因而可以采用OLS回歸方法求解新的模型中的回歸系數(shù)，并給出Z的估計(jì)值。然后，我們利用反變換式（3），就可以反算出“出現(xiàn)概率”p的估計(jì)值，并進(jìn)行統(tǒng)計(jì)檢驗(yàn)。

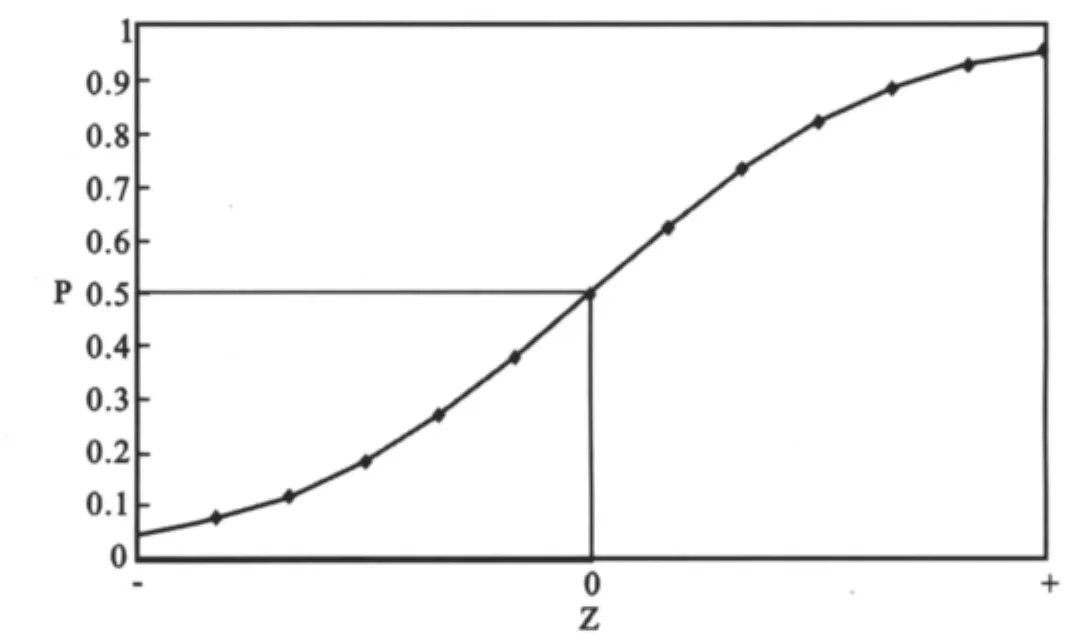
圖1 發(fā)生比的對(duì)數(shù)Z與概率p之間的關(guān)系曲線

要指出的是，通常對(duì)得到的回歸方程的顯著性檢驗(yàn)、復(fù)相關(guān)系數(shù)和F統(tǒng)計(jì)檢驗(yàn)的解釋與判斷等，在這種情況下都是沒有意義的。一種簡(jiǎn)便而有效的方法是采用“正確率C”（Correct rate）來檢驗(yàn)，即通過回歸模型對(duì)樣本中的每一個(gè)樣品的因變量進(jìn)行評(píng)估，檢查有多少個(gè)樣品能夠以此模型正確估計(jì)，然后以其占樣品總數(shù)的百分比作為“正確率C”，進(jìn)而對(duì)回歸方程作出評(píng)價(jià)，判斷是否能夠通過檢驗(yàn)，并加以應(yīng)用［8］。

至于是否“正確”，則可以預(yù)先選定一個(gè)“閾值”，以此將因變量的預(yù)報(bào)值加以劃分，并向兩極“推移”，形成邏輯變量的“真”（True）與“假”（False），或者二分類定性變量的“合格”與“不合格”等。

在模糊數(shù)學(xué)中，認(rèn)為隸屬度在0.5附近時(shí)，事物是最模糊不清的。我們也常以0.5作為閾值，即認(rèn)為＞0.5是“真”（True），≤0.5是“假”（False）。

按照這樣的約定，在實(shí)際操作時(shí)，就可以將Z的估計(jì)值為負(fù)的或?yàn)榱愕臍w為一類，即“不合格”；而將Z的估計(jì)值為正的歸為另一類，即“合格”。從而重新形成二分類定性變量，以供分析和討論。

2 Logistic回歸模型示例

我們以一種陶瓷磚的抗熱震性的測(cè)試結(jié)果作為示例，來演示利用Logistic回歸模型建立該性能與組成之間關(guān)系的數(shù)模的過程。

試驗(yàn)是在預(yù)先選定的3種元配料為頂點(diǎn)的單純形中，按3因子5分段的單純形格子設(shè)計(jì)方案｛3，5｝給出的21個(gè)試驗(yàn)點(diǎn)上進(jìn)行的。回歸方程的右部是廣義線性形式。實(shí)際采用的是自動(dòng)滿足混料約束條件的3次不完全多項(xiàng)式［9～10］。按照相應(yīng)的國家標(biāo)準(zhǔn)測(cè)定了21組不同組成（原料配合比）試樣的抗熱震性，測(cè)試結(jié)果見表2。

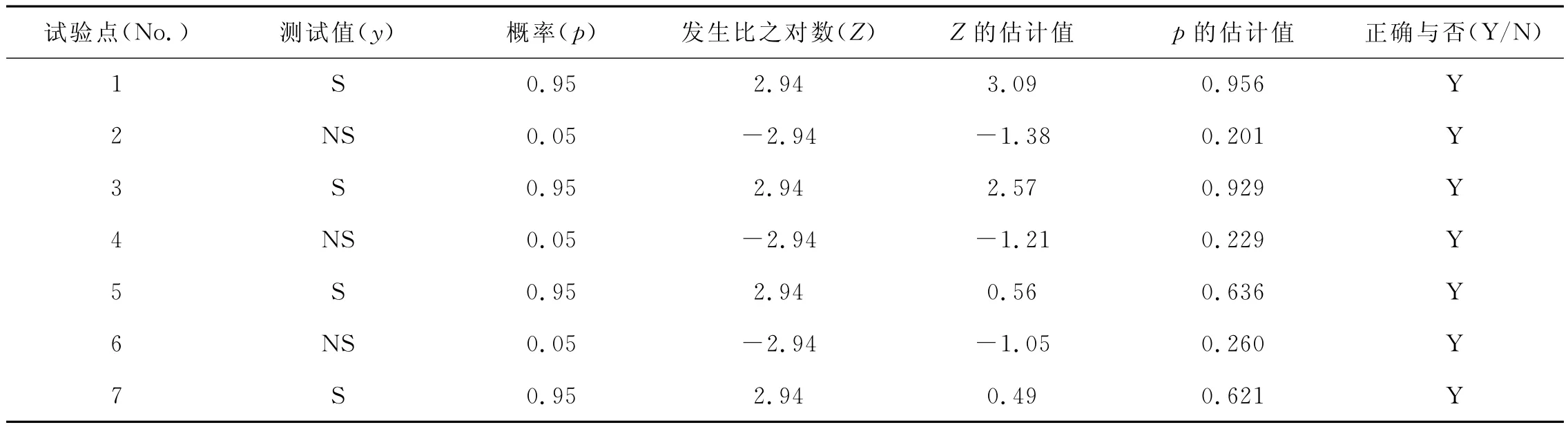
表2 陶瓷磚抗熱震性測(cè)試值和建模結(jié)果

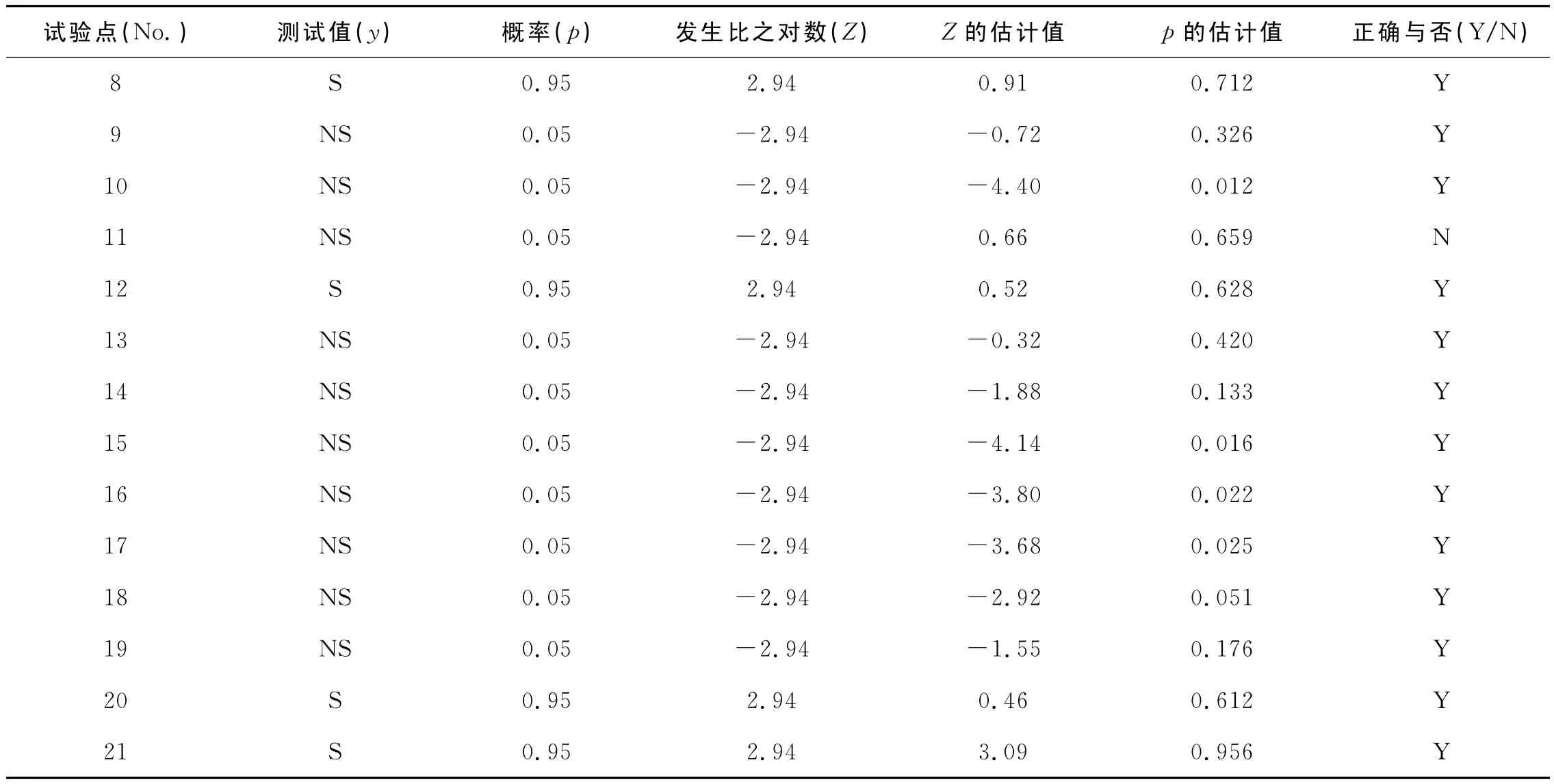
續(xù)表1

對(duì)于這些二分類定性變量，我們采用Logistic回歸模型來建立性能與組成之間關(guān)系的數(shù)模。取對(duì)應(yīng)于“合格”的概率p為0.95，因而不合格之概率即應(yīng)取作（1－p）＝0.05。再按式（2）進(jìn)行正變換，對(duì)應(yīng)于“合格”的Z值為2.94，而對(duì)應(yīng)于“不合格”的Z值為 －2.94。代入式（1）的回歸方程，用OLS回歸方法求解，可得到一組回歸系數(shù)b0和bi，以及Z的估計(jì)值。最后，再按式（3）進(jìn)行反變換，即可得到概率p的估計(jì)值。

如果選定“閾值”為0.5，接下來就可以檢視利用數(shù)模得到的估計(jì)值，在“二分類”意義下是否正確。結(jié)果顯示在21個(gè)試驗(yàn)點(diǎn)中，對(duì)其中20個(gè)點(diǎn)的預(yù)報(bào)和估計(jì)是正確的，只有第11點(diǎn)的不符合。故正確率比較高，這說明利用Logistic回歸模型是成功的。

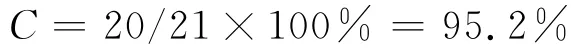
3 結(jié)語

在陶瓷制品的性能測(cè)試中，有一些是采用二分類定性變量來表征的。要想建立這些性能與組成之間關(guān)系的數(shù)學(xué)模型，采用OLS回歸方法是不可取的。這就需要一種新的回歸模型。筆者介紹的Logistic回歸模型及方法，是其中良好的一種。經(jīng)過試用，證明在其材料科學(xué)與工程領(lǐng)域中同樣適用，有較好的使用效果，并希望在使用過程中不斷地改進(jìn)與完善。

1 上海師范大學(xué)數(shù)學(xué)系.回歸分析及其試驗(yàn)設(shè)計(jì).上海：上海高教出版社，1978

2 高力明.材料成分及其制備工藝條件的CAD.陶瓷導(dǎo)刊，1992（3）：25～28

3 高力明.元配料在材料性能之建模尋優(yōu)方面的應(yīng)用.全國性建材科技核心期刊——陶瓷，2005（9）：8～11，15

4 GB／T 3810.9－2006，陶瓷磚試驗(yàn)方法 第9部分：抗熱震性的測(cè)定

5 GB／T 3810.12－2006，陶瓷磚試驗(yàn)方法 第12部分：抗凍性的測(cè)定

6 GB／T 3298－91，日用陶瓷器熱穩(wěn)定性測(cè)定方法

7 高力明.我國陶瓷窯爐產(chǎn)業(yè)及其市場(chǎng)的形成與發(fā)展.中國陶瓷，2004（增刊）：7～9

8 郭志剛.社會(huì)統(tǒng)計(jì)分析方法－SPSS軟件應(yīng)用.北京：中國人民大學(xué)出版社，1999

9 高力明.元配料之概念.陶瓷學(xué)報(bào)，2003，24（1）：25～30

10 朱偉勇，等.最優(yōu)化設(shè)計(jì)理論與應(yīng)用.沈陽：遼寧人民出版社，1981

TQ174.75 文獻(xiàn)表示碼：A

1002－2872（2012）08－0020－03

高力明（1941－），教授；研究方向?yàn)樘沾筛G爐熱工及計(jì)算機(jī)在材料科學(xué)領(lǐng)域的應(yīng)用。