《數理統計》中假設檢驗知識點的教學探討
李正耀,何先平
(長江大學信息與數學學院,湖北 荊州 434023)
《數理統計》中假設檢驗知識點的教學探討
李正耀,何先平
(長江大學信息與數學學院,湖北 荊州 434023)
分析了《數理統計》課程中假設檢驗知識點教學過程中學生經常出現的一些問題,提出在實際教學中采用直觀、聯想與類比的教學方法,讓學生正確理解假設檢驗的原理與方法,并給出了假設檢驗中假設選取的2條原則。
假設檢驗;假設選取;類比教學法
假設檢驗是統計推斷的2大核心任務之一,在統計中具有非常重要的意義。讓學生理解假設檢驗的基本原理,學會在實際中正確使用假設檢驗法,對于提高學生的綜合素質及培養學生解決實際問題的能力是非常重要的。但一般而言,工科《概率論與數理統計》課程[1]的假設檢驗部分在實際教學中,往往過于程式化,學生對假設檢驗的原理不清楚,只知道有若干個難記的公式,遇到實際假設檢驗問題時,卻不知道如何正確使用;檢驗之初不知如何選擇適當的命題作為原假設與備擇假設;由樣本觀測值作出檢驗結論時,對于“拒絕原假設”與“接受原假設”的準確含義不能真正理解。下面,筆者在實踐教學中就上述問題進行了探討?。
1 以生動直觀的例子理解假設檢驗的基本思想
例1一南北交通干線全長10km,公路穿過一隧道,隧道南面3.5km,北面6.5km,在剛通車的一個月中,隧道南發生了3起互不相關的交通事故,而北面沒有發生交通事故,據此能否認為隧道南面的公路更容易發生交通事故[2]?
分析隧道將公路分為2段:隧道南3.5km,北面6.5km,記p表示一起交通事故發生在隧道南面的概率,如果每起交通事故在這段公路上每一點等可能發生,則p=0.35(視為原假設H0);而p>0.35(視為備擇假設H1)表示隧道南面的公路更容易發生交通事故。用W表示3起交通事故發生在隧道南,假定每起交通事故在這段公路上每一點確實是等可能發生(H0為真),則每一起事故發生在隧道南的概率都是0.35,由于3起事故是相互獨立的,則P(W)=0.353≈0.05,W是一個小概率事件,一般不會發生,既然它發生了,就有充足的理由否定該假定(拒絕H0),認為隧道南面的公路更容易發生交通事故。
從上述例子中,容易理解假設檢驗的過程中包含2個重要思想:①反證法思想。為了檢驗原假設H0是否正確,首先假設H0為真,看由此能推出什么結果,如果導致一個不合理的結果出現,則表明“假設H0為真”是錯誤的,由此應當拒絕原假設H0;如果沒有導致不合理的現象出現,則不能認為“假設H0為真”是錯誤的,只好選擇接受H0。②小概率原理。數理統計中的小概率原理是指“一次試驗中,小概率事件是幾乎不會發生的”,在原假設H0成立的條件下,樣本觀測值(x1,x2,…,x2)落入拒絕域W是一小概率事件,P{(x1,x2,…,x2)∈W}=α,應當是“不容易發生的”,如果該事件發生了,則有充分的理由認為原假設H0不正確。
2 假設檢驗中注意假設的選取原則
2.1原則1
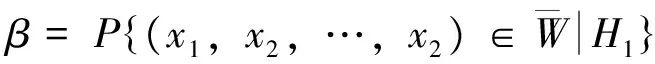
原則1如果想強烈地支持某一命題,則應將這一命題作為備擇假設,而將它的否命題作為原假設。
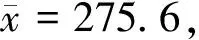
分析這是一個剛建成投產的工廠,人們對它生產的產品的質量狀況沒有任何認識,工廠也希望以自己產品的優良品質贏得用戶對它的充分信賴,為了能以充足的理由說明該廠的質量可靠,因此,應作如下假設:H0:μ≤225?H1:μ>225。
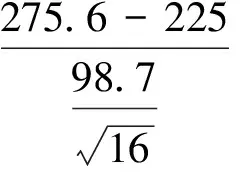
如果提出的是另外一種形式的假設,即H0:μ≥225?H1:μ<225,還是使用t檢驗統計量,在顯著性水平α=0.05時,拒絕域為{t<-1.753},檢驗統計量的觀測值是相同的,即t=2.05,樣本觀測值落入接受域中,將由此作出接受原假設的判斷。值得注意的是,這時雖然作出了“該廠生產的產品符合國家標準”的判斷,但理由是不充分的!
2.2原則2
由于在假設檢驗中,當原假設為真時,拒絕原假設是如此的不易(必須要有充足的理由),因此,假設檢驗具有一種強烈的保護原假設的傾向。
原則2將久已存在的、不能輕易被否定的命題或成見作為原假設。
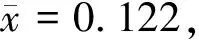
對這一實際問題,分別提出2種不同形式的假設,考察它們的結論有何差異。
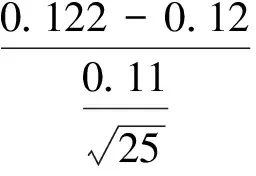
2)假設Ⅱ 考慮作假設II:H0:μ≥0.12?H1:μ<0.12。還是使用t檢驗統計量,在顯著性水平α=0.05時,拒絕域為{t<-1.711},檢驗統計量的觀測值還是t=0.091,樣本觀測值落入接受域中,將由此作出判斷:“該廠生產的微波爐輻射量指標不符合標準”(準確的說法是:“沒有理由認為該廠生產的微波爐輻射量指標符合標準”) 。
對這同一組樣本觀測值,2種形式的假設檢驗卻得到了完全相反的結論,這在實際中并不少見,采信何種判斷就必須要依賴于人們對該對象的經驗與成見。如果該廠生產的微波爐質量一向良好,根據選取假設的第2條原則,應充分保護這種經驗與成見,將“質量良好”作為原假設,即應采用假設Ⅰ,樣本觀測值顯示:沒有充分理由認為該廠生產的微波爐輻射量指標不符合標準。因此,最終的結論是該廠生產的微波爐輻射量指標符合標準;反之,如果該廠一向質量不可靠或是剛建成投產的新廠,則應采用假設Ⅱ,最終的結論是:該廠生產的微波爐輻射量指標不符合標準。
3 聯想與類比:假設檢驗與司法判決
司法判決在某種意義上也是一種假設檢驗,結合司法實踐中的一些案例,可以非常形象直觀地幫助學生正確理解假設檢驗中的基本原理。以刑事訴訟為例,有罪推定是指先將一個人的行為定為有罪(即原假設為:此人有罪),然后圍繞其犯罪不可否認的定論去尋找法律和事實依據;無罪推定是與有罪推定相對而言的(該檢驗的原假設為:此人無罪),犯罪嫌疑人,被告人在未經法院判定有罪的情況下,應推定其無罪。對于某一犯罪嫌疑人或被告人,使用同樣的證據,采用“有罪推定原則”進行判決與采用“無罪推定原則”進行判決,結果可能是完全不同的,可以把這一點完全讓學生對照例3中的假設檢驗問題細細體味,進而得出結論:現代文明社會的司法制度采用“無罪推定”,就是要充分保護“無罪”這個原假設,起到保障人的自由、生命、榮譽與權利,所以說“無罪推定”是偉大的政治文明,是最符合人性的偉大法律原則。另一方面,由假設檢驗可以知道,如果作出拒絕原假設的判斷,理由是充分的,而作出接受原假設的判斷,理由是不充分的,將該原理應用于刑事訴訟,在無罪推定原則下,如果某人被判為“有罪”(拒絕原假設),則該嫌疑人一定是罪有應得;如果某人被判為“無罪”(接受原假設),則該嫌疑人未必沒有犯案。
在假設檢驗的教學中,通過上述這種聯想與類比,可以使得看似枯燥單調的公式與規則,變得更直觀、更生動有趣,起到開闊學生視野,培養學生在別人看不到數學的地方用數學的眼光發現數學、應用數學。類似這樣的訓練,對提高學生的綜合素質,培養學生的創新意識和創新能力將發揮重要作用。
[1]盛驟,謝士千,潘承毅.概率論與數理統計[M].第4版.北京:高等教育出版社,2008.
[2]何書元.數理統計[M].北京:高等教育出版社,2012.
[編輯] 洪云飛
10.3969/j.issn.1673-1409(N).2012.12.059
N4
A
1673-1409(2012)12-N175-03

