小學數學化歸思想研究述評

馬 旭

(云南民族大學 教育學院，云南 昆明 650500)

小學數學化歸思想研究述評

馬 旭

(云南民族大學 教育學院，云南 昆明 650500)

對有關化歸思想在小學數學中的滲透的文獻進行了分類整理和歸納分析,分別就化歸思想在小學數學教材、教學、解題中的滲透這三方面進行了文獻梳理,總結了當前化歸思想在小學數學中滲透所取得的成果及存在的不足。

化歸思想；小學數學

一 化歸思想簡介

“化歸”從字面上看，指的就是轉化和歸結的意思。而在數學方法論中，化歸指的是數學家們把待解決的或未解決的問題，通過一定的轉化過程，歸結到一類已經能解決或者比較容易解決的問題中去，最終獲原問題的解答的一種手段和方法。化歸方法同時也稱為化歸原則。

下面我們看一個例子：

有人提出了這樣一個問題：“假設在你面前有煤氣灶、水龍頭、水壺和火柴，你想燒開水，應當怎樣去做？”對此某人回答說：“在壺中灌上水，點燃煤氣，再把壺放到煤氣灶上。”提問者肯定了這一回答；但是，他又追問道：“如果其他的條件都沒有變化。只是水壺中已經有了足夠多的水．那你又應當怎樣去做?“這時被提問者往往會很有信心地說：“點燃煤氣，再把水壺放到煤氣灶上。”但是，提問者指出，這一回答并不能使他滿意，因為，更好的回答應當是：“只有物理學家才會這樣做，而數學家們則會倒掉壺中的水，并聲稱我把后一問題化歸為前面所說的問題了。”(史久一,朱梧槚，1989)

這個故事看起來像一個笑話，但是它正好反映出了數學解題過程中人們普遍采用的一種手段與方法，也就是通過一系列的轉換的方法與手段把遇到的新問題轉化為過去曾經解決過的問題，依托曾經解決過的問題來解決新的問題。

在數學史上，有不少數學家也從各種不同的角度對化歸方法進行過論述。笛卡爾在《指導思維的法則》一書中就曾提出過如下的“萬能方法”：

第一，將任何種類的問題化歸為數學問題；

第二，將任何種類的數學問題化歸為代數問題；

第三，將任何代數問題化歸為方程式的求解。

因此在小學階段，將化歸思想介紹給學生，讓學生掌握這一方法顯得尤為重要。我們不僅要向學生傳授基本知識，基本技能，更重要的是使學生掌握更多的數學思想，數學方法。這將有助于學生今后的學習與發展。

二 化歸思想在小學數學中的滲透

化歸方法是一種通過轉換間接解決問題的方法。它在數學問題解決中的作用就在于轉化，轉化問題是解決問題的關鍵，轉化的思想就是化歸的思想。問題的解決過程就是不斷地發現問題、分析問題，直至化歸為一類已經能解決或者比較容易解決的問題的過程。化歸方法在數學問題解決中具有十分重要的意義。這已經被很多人所意識到。尤其是將化歸思想滲透到小學數學中，已經被越來越多的人所重視。以下是化歸思想在小學數學中的一些具體運用。

1．化歸思想在小學數學教材中的滲透。

化歸思想體現在小學數學教材的各個方面。

(1)在數與代數方面。結合數的認識教學，滲透化歸數學思想方法。“數的認識來源于生活，又應用于生活”(葉錦紅，林丹，2010)。小學數學教材選取問題的范圍大都來源于學生密切接觸的現實生活，在此我們可以隨便舉個例子 。

例如，人教版小學數學三年級下冊第7課《小數的初步認識》。

圖1①

對小數的認識從學生密切接觸的現實生活入手，學生開始的時候不知道小數這一概念，但是在現實生活中肯定是買過東西的。并且商品的價格不全是整數，因此通過教材這一媒介，將學生們現實生活中經常遇到不加注意的材料聯系起來。并且通過這樣一種從生活中來，并應用于生活的學習，加深對于知識的學習。

(2)空間與圖形。“對于平行四邊形面積計算的研究課例中已具體說明，主要通過現實問題具體化到抽象問題，然后在抽象與具體間建立聯系，從而實現抽象向具體的化歸，同時利用割補、平移等化歸途徑，自主將復雜問題簡單化成求長方形的面積”(葉錦紅，林丹，2010)。圖形的計算就在于圖形的變換，恰當的變化與轉化使得圖形的計算變得尤為簡便。而在小學階段，對于新圖形的認識，最好的辦法就是將它轉化為已經學過的圖形。

圖2②

正如平行四邊形的學習一樣，復雜圖形的學習很重要的一個方法就是將其分解成簡單圖形，正是這種化繁為簡的方法，為以后的幾何學習打下了一定的方法基礎。

正如前面所談到的化歸思想大量地滲透到了小學數學教材中。所以，“教師要認真研讀教材，透過顯性的教學內容挖掘隱藏的數學思想方法”。(李放，2010)

2.化歸思想在小學數學教學中的滲透。

首先，在小學數學教學中滲透化歸思想，可以通過“創設問題情境”的方法。(李放，2010；葉錦紅，林丹，2010)通過創設一定的問題情境，提高同學們的積極性。將一些抽象的問題具體化，使得同學更容易理解所要學習的內容。

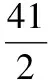
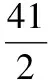
針對兩種情況,再分別算出各跳了幾次, 確定誰先掉人陷阱,問題就基本解決了。

上面的思考過程,實際上是把一個實際問題通過分析轉化、歸結為一個求“ 最小公倍數” 的問題, 即把一個實際問題轉化、歸結為一個數學問題。因此可以通過創設一定的問題情境在教學過程中將化歸思想融入問題之中。使學生清楚地掌握化歸思想。

其次，“在學生知識的發生過程中滲透化歸思想”。(李放，2010)也就是人們通常所說的在知識的產生、推導與轉化過程中滲透化歸思想。

例如，平行四邊形的面積計算：長方形的面積是長乘寬，那么平行四邊形的面積該如何計算呢？在同學們剪拼的過程中，把平行四邊形轉化成長方形，并引導他們思考：平行四邊形與拼成的長方形有什么關系？最后得出：平行四邊形的面積=底×高。

通過轉化，將未知的問題轉化為已知的問題，最后達到解決問題的目的。這一過程不僅是一個得到最終答案的過程，更為重要的是使學生學會了一種解決問題的方法。學會這一方法之后在今后的學習中碰到類似的問題，便能夠輕而易舉地解決了。對于教師的教學“不在于教什么，而真正在于怎樣教”(Ricardo Cantoral amp; Rosa M. Faran,2003)。

3.化歸思想在小學數學解題過程中的滲透。

數學學習一個主打的方面便是數學問題的解決——解題。數學無論從學習入手，還是最終學習情況的考核，主要就是看解題的能力。化歸思想也正是在解題過程中才能充分體現出來。因此，大量的目光也就聚焦到數學問題的解決這一領域上來。

“在各類試題的學練中, 要用符號思想、模型思想等, 使學生正確、靈活、迅速地掌握各種運算法則、性質、定律、順序等,使試題的學練成為學生解決各類實際問題的可靠工具”。(安君麗，2001)“在解決問題中體驗數學思想方法，運用數學思想方法可以更有效地解決問題”。(李放，2010)人們不但意識到了化歸思想在解題過程中的作用，同時也總結出了一些化歸思想在解題過程中的方法。“即把一個實際問題轉化、歸結為一個數學問題”。楊莉(2005)也就是通常所說的數學建模，將生活中的問題利用數學方法加以解決。其本質也體現了學以致用的一般原則。而吳生蓮(2009)則將其具體化為“數據轉化、圖形轉化、題型轉化”三大類型。可以說是比較具體地分析了在小學數學解題過程中存在的各類情況。

但在利用化歸思想的同時我們也必須明確一點“這種化歸思想不同于一般所講的‘轉化’‘轉換’。它具有不可逆轉單向性。”(楊莉，2005)

三 化歸思想滲透到小學數學的問題

通過上面的介紹，我們大體明確了化歸思想滲透到小學數學中的三種方式。但是我們在具體運用化歸思想的時候還得注意一些問題。

第一，使未知問題熟悉化。我們使用化歸思想解決問題時必須要將我們所遇到的新問題轉化為一個或幾個我們所熟悉的問題，即將陌生的問題轉化為我們已經熟悉的，在過去的時間內已經解決過的問題，這樣一來，我們就能夠將待解決的問題依托于我們曾經使用過的方法來解決。同樣，我們在教學生的時候也應該將新問題轉化為學生以前學習過的問題，會的問題。這樣一來也能把新舊問題連接起來使知識產生連貫性，系統性。從教材的編排上我們也能夠看出來，小學數學主要圍繞三大部分：數與代數、空間與圖形、數理統計。從一年級到六年級都圍繞著這三大部分。通過問題的轉化便能將知識以一個脈絡連接起來。

第二，將問題簡單化。化歸思想是一種解決問題的手段與方法，因此，我們在使用過程中肯定應該選一條捷徑來走，原問題困難，我們就教給學生想辦法將其簡單化，從上面的例子我們也可以看出來，將平行四邊形轉化為三角形與矩形時就遵循了這樣一個原則。簡單化原則也提醒我們在使用化歸思想時，不要將原問題復雜化，原來很簡單的問題，我們不能反倒將其轉化為一個更困難的問題去求解。

第三，將問題具體化。有些問題很抽象，我們可以使用一些諸如數形結合的方法，將一些不明顯、比較抽象的問題使用圖形來表示，來解決。這樣一來，我們便可以將原問題清晰具體地反映出來，通過具體問題的解答，將原問題加以解決。這一原則在下面具體闡述化歸思想的應用過程中將予以體現。

第四，正難則反。正難則反，也就是我們通常意義上的反證法。原問題的條件給了我們一種思路，但是依靠這一思路我們很難將問題解決了，因此，我們可以換一種思路，原問題讓我們向前走，我們可以想想，如果向后退情況會是什么樣呢？在我們解決一些問題過程中我們可以使用例如反證法這樣的一些手段，將問題轉化到問題的另一面加以解決。

四 總結

通過梳理我們已經明確了化歸思想滲透到小學數學中的三種方式：通過教材的編寫滲透，通過教師的教學滲透以及通過解題過程滲透。通過這三種方式，可以很好地使學生掌握化歸思想這一重要的思想方法。這也在一定程度上告訴我們可以從哪幾個方式入手將化歸思想傳遞給學生。通過課堂，可以更好地發揮教師的主導地位與學生的主體地位，使學生掌握化歸思想。

但同時我們也能夠看出目前化歸思想在小學數學中的滲透主要是靠教師的知識傳遞。也正是在教師傳授的過程中出現了很多問題，這便是教師的滿堂灌，使學生盲目接受知識，而不加思考。因此，使學生掌握化歸思想只有發揮學生的主動性。培養讓學生在自學過程中，自覺地使用化歸思想。這樣才能最大限度地發揮學生的創造性思維。鼓勵學生自覺運用化歸思想將是以后研究的重點方向。

同時，如今是一個學習型的社會，知識的學習也不能僅僅靠個人的埋頭苦讀，而是需要組成一定的學習團隊，形成一定的學習小組。鼓勵學生形成一種合作學習的學習方法，讓學生對于新的學習問題形成一種“合作的視角”(Cindy E. Hmelo-Silver ，Ellina Chernobilsky amp;Rebecca Jordan，2008)，將是今后教學的重中之重。也正因為如此，化歸思想的滲透同樣需要教師有意識地在班級里組建學習小組，通過小組成員間的相互學習來掌握化歸思想。這也將是今后關注的焦點之一。

注釋

①http://www.pep.com.cn/xxsx/xxsxjs/xs3b/xs3bkb/200703/t20070314_339024.htm.

②http://www.pep.com.cn/xxsx/xxsxjs/xs4a/xs4akb/200704/t20070411_388604.htm.

[1]史久一,朱梧槚.化歸與歸納·類比·聯想[M]．南京：江蘇教育出版社，1989：141-190.

[2]成尚榮. 學會數學地思維——小學數學教學案例解讀[M].南京：江蘇教育出版，2001：148-186.

[3]張甦，朱英.數學思想方法[M].上海:上海科學普及出版社，2009:26-87.

[4]安君麗.新世紀小學數學教學的精髓[J].教育實踐與研究,2001(11),53.

[5]楊莉. 小學數學教學中如何滲透數學思想方法[J].科學咨詢(教育科研), 2005(03): 51.

[6]陳桂娣. 數學思想方法: 小學數學教學不可忽視的靈魂[J].黑龍江科技信息,2007(03): 115.

[7]于占武.化歸思想在解題中的應用[J].赤峰學院學報，2007(10): 24-25.

[8]凌健.化歸思想在數學解題中的應用[J].安慶師范學院學報 ，2008(2): 511.

[9]吳生蓮.例談化歸思想方法在解題中的滲透[J].小學教學參考(數學)，2009(10): 59.

[10]李放.滲透數學化歸思想提高問題解決能力[J].新課程研究 ,2010(06):122-124.

[11]葉錦紅、林丹. 數學化歸思想在小學數學教學中的應用[J].科研縱橫 , 2010(08)：26-27.

[12]Ricardo, C. , amp; Rosa, M. F.(2003).Mathematics education:a vision of its evolution. Educational Studies in Mathematics， 53:255-270.

[13]Cindy E. Hmelo-Silver , Ellina C. amp; Rebecca J.(2008). Understanding collaborative learning processes in new learning environments. Instructional Science， 36:409-430.

ClassNo.:G623.5DocumentMark：A

(責任編輯：宋瑞斌)

ReviewoftheIdeaofConversioninMathematicalEducationinPrimarySchool

Ma Xu

Firstly, classification and an inductive analysis are made through systematic research literature of the permeation of the idea of conversion in mathematical education in primary school. Secondly, a literature review of permeation is made in the following three aspects: 1) textbook 2) instruction and 3) solving problems in mathematical education in primary school. Finally, achievements and Limitations in current studies on the permeation of the idea of conversion in mathematical education in primary school are summarized.

idea of conversion;mathematical education in primary school

馬旭，碩士，云南民族大學教育學院。

1672-6758(2012)09-0007-3

G623.5

A