基于中弧線的空心渦輪葉片壁厚計算方法研究

劉金鋼 卜 昆 楊小寧 程云勇 董一巍

西北工業大學現代設計與集成制造技術教育部重點實驗室，西安，710072

0 引言

渦輪葉片是航空發動機的關鍵部件之一，由于其內部冷卻結構復雜，且長期服役在復雜循環熱應力環境條件下，故對其氣動外形、性能強度及尺寸精度要求高，而葉片的壁厚是關系到其性能和精度的一個重要參數，因此對葉片壁厚的準確測量有著非常重要的意義。在葉片的檢測方法中，傳統的方法主要有超聲波法［1］和電渦流法，其中超聲波法受超聲波測厚儀影響，存在測量盲區和測量下限的限制，而電渦流法受渦流測厚儀法向找準、測頭半徑補償，以及工件尺寸大小等因素的影響，測量精度低，無法達到公差要求。在實際壁厚測量中，一般需要測量葉身的3～5個關鍵截面，大多使用超聲波測厚儀沿葉片表面測量點的法線方向進行測量，該方法不易確定法線方向，誤差較大，容易放大壁厚。文獻［2－5］提出的基于ICT（industry computerized tomography）圖像的壁厚檢測方法，通過像素標定技術對截面內外輪廓進行測量，其測量精度較高，但花費時間長，成本高。

為了克服傳統壁厚測量的不足，本文以CT（computerized tomography）測量數據為基礎，提出一種基于中弧線的空心渦輪葉片壁厚計算方法，采用等距法計算外輪廓中弧線，根據壁厚定義計算空心葉片壁厚。與傳統方法相比，該方法測量精度高，適用范圍廣。

1 CT數據的采集和處理

空心渦輪葉片的壁厚是指內外輪廓之間的厚度。針對渦輪葉片內輪廓無法測量的特點，采用實驗室的錐束CT測量設備進行切片圖像采集，通過檢測分析軟件對切片圖像進行圖像處理，可得到渦輪葉片的點云模型。

1.1 葉片CT數據與葉片CAD配準

葉片CT測量數據配準定位精度的高低直接影響壁厚測量精度，要準確測量空心葉片的壁厚必須選擇精度高的配準方法。目前針對配準問題主要有三類方法：基于標記的配準方法、基于特征的配準方法［6］、基于表面點集的配準方法。根據渦輪葉片點云數據的特點，本文采用第三類方法，選擇SVD＿ICP算法。該算法是一種經典的模型匹配算法［7］。首先在模型之間建立一些最近點的點對關系，然后以距離平方和為目標函數，不斷地迭代，求解兩模型之間的旋轉矩陣R和平移矩陣T，使得目標函數取得最小值，最后使兩個模型緊密貼合。

1.2 截面線獲取

經過配準后，渦輪葉片點云模型的測量坐標系統與渦輪葉片CAD模型的設計坐標系統對應起來，要計算渦輪葉片對應點處厚度，必須獲得對應點處的截面。采用Geomagic Qualify 11軟件的平面截取功能，得到渦輪葉片的截面點云數據，運用二次提取法［8－10］對截面線數據點進行排序、粗提取和精提取等處理，最后得到CT截面線輪廓，如圖1所示。

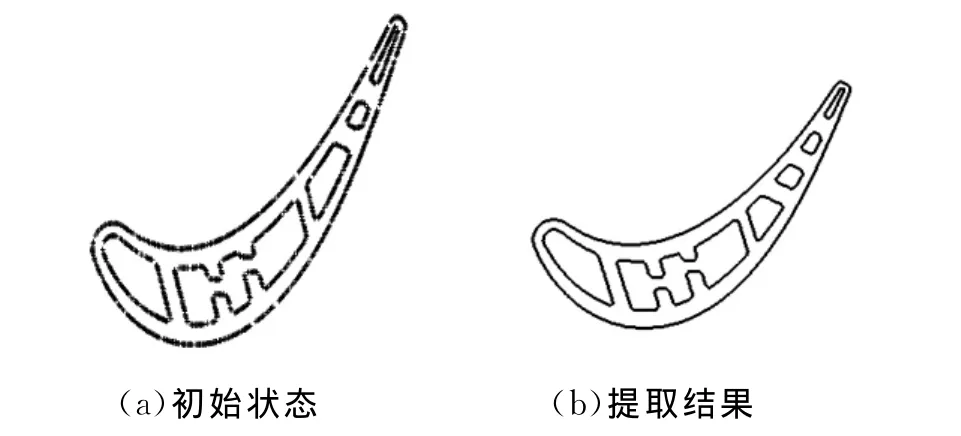
圖1 CT截面線輪廓提取

2 葉片壁厚計算

2.1 空心渦輪葉片壁厚相關定義

為了減小誤差，提高精度，對內外輪廓的截面線進行擬合，計算外輪廓的中弧線，求取內輪廓（不包括加強肋的外輪廓）上的點P2到中弧線的最短距離的點O，以點O為圓心，作點O的內切圓，內切圓與外輪廓的切點為P1，連接P1和P2，P1和P2間的距離即為切點P1處的壁厚，如圖2所示。

圖2 空心葉片壁厚定義示意圖

2.2 基于中弧線計算壁厚

白瑀等［11］、王軍偉［12］提出了兩種計算中弧線的方法：等半徑法和等角度法。這兩種方法都要計算切線或法線，要是沒有曲線的連續模型，就必須用差商來代替，而這樣處理誤差會較大。采用內切圓法計算時，法線方向可能與葉盆（或葉背）曲線存在多個交點，采用等角度法計算時，必須將前一個內切圓的半徑作為下一個內切圓半徑的初始值，存在誤差傳播。中弧線上的點一定是截面線上某兩個不同點的法線的交點，而且它到這兩個點的距離相等，因此中弧線上的點就是截面線等距線的自交點。基于此，本文采用等距線的方法求解中弧線。

利用等距線法求中弧線，首先運用二次提取法得到截面線輪廓，然后通過調整葉盆和葉背偏置距離得到等距線交點，最后對這些葉盆和葉背交點進行排序、插值得到光順的中弧線。具體求解步驟如下。

（1）由于有理三次Bezier樣條曲線可以精確地表示二次曲線和計算等距線，因此將葉身外截面線的葉背Cb（θ）離散為n＋1個插值點，構造的n段G2連續分段有理三次Bezier樣條曲線記為Bi（u）（i＝1，2，…，n），其沿內法線方向的單位法向量為Ni（u），則外截面線的葉背等距線為

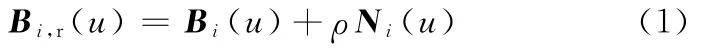
式中，ρ為偏置距離。

（2）同理，將葉身外截面線的葉盆Cp（θ）離散為n＋1個插值點，構造的n段G2連續分段有理三次Bezier樣條曲線記為Pi（u），其沿外法線方向的單位法向量記為Wi（u），則外截面線葉盆等距線為

（3）求解下式，以判斷外輪廓線葉身和葉背等距線是否有交點：

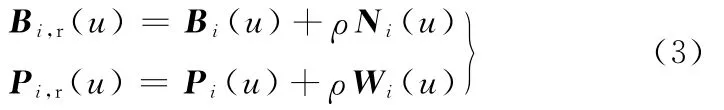
分三種情況分析：①當偏置距離ρ小于最小壁厚時，沒有交點。② 當取ρ為最小壁厚時，令ρ←ρ＋Δρ，其中，Δρ為偏置距離的增大步長，可取為葉片數據測量精度的1／20。增大偏置距離ρ，求解式（3）得到交點，該點即為內切圓圓心，此時ρ即為內切圓半徑。③當偏置距離ρ增大到一定程度時，葉盆和葉背的等距線就不存在交點，此時ρ應該是葉片最大厚度ρmax，可用葉片設計厚度ρmax作為偏置距離的上限，當ρ≥ρmax時，求解結束。

（4）將求解方程得到的所有內切圓圓心記為Oj（j＝1，2，…，m），經過處理后得到中弧線，如圖3所示。將內切圓半徑記為Rj，求解下式得到內切圓與截面線葉背Cb（θ）切點：

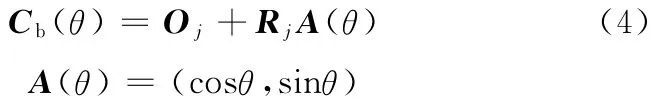
切點記為Pbj（xbj，ybj）。求解下式得到內切圓與截面線葉盆Cp（θ）切點：

此切點記為點Ppj（xpj，ypj）。

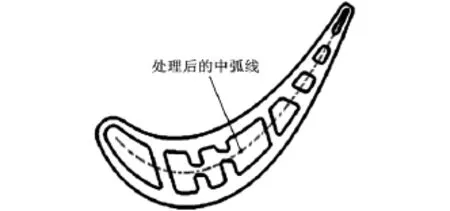
圖3 處理后的中弧線示意圖

（5）將內輪廓截面線離散成大量的數據點，記為Nk（xk，yk）（k＝0，1，…，h），求解點Nk到中弧線的最短距離Dk，得到中弧線上的點，即內切圓圓心Oj，根據步驟（4）的切點Pbj（xbj，ybj）和Ppj（xpj，ypj），求解下式：

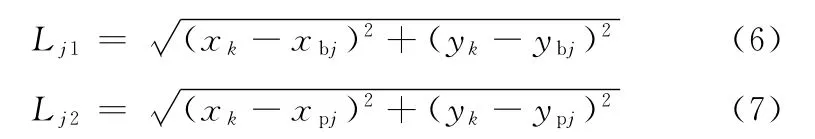
如果Lj1≥Lj2，則Lj2為Pbj（xbj，ybj）點的壁厚；如果Lj1＜Lj2，則Lj1為Ppj（xpj，ypj）點的壁厚。

3 空心渦輪葉片壁厚算法驗證與分析

本文討論的基于中弧線的壁厚計算方法，是在UG平臺下基于UG open API函數庫編程實現的。以空心渦輪葉片的CT點云數據為對象，分別選擇五個截面進行壁厚計算，得到相應的壁厚，其三維分布如圖4所示。

圖4 某復雜空心渦輪葉片各截面壁厚三維分布圖

其五個截面的壁厚分布如圖5～圖9所示。由圖5～圖9可知，空心渦輪葉片的壁厚在葉背凸峰和葉盆凹峰處最大，向前緣和后緣方向依次減小，在沒有內輪廓的地方突然增大，這是由于存在加強肋的緣故。

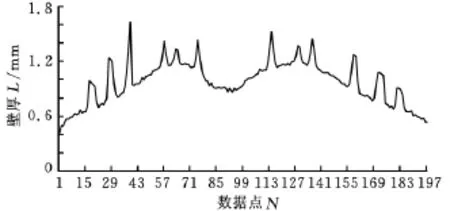
圖5 某復雜空心渦輪葉片截面1壁厚分布圖

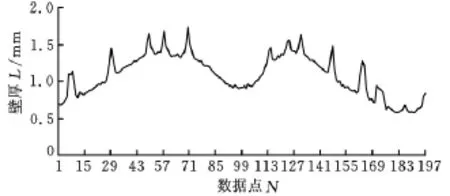
圖6 某復雜空心渦輪葉片截面2壁厚分布圖

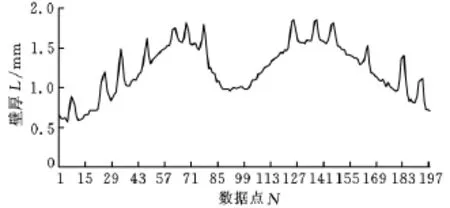
圖7 某復雜空心渦輪葉片截面3壁厚分布圖

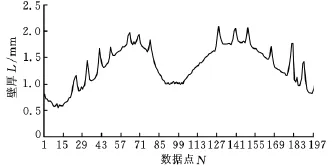
圖8 某復雜空心渦輪葉片截面4壁厚分布圖

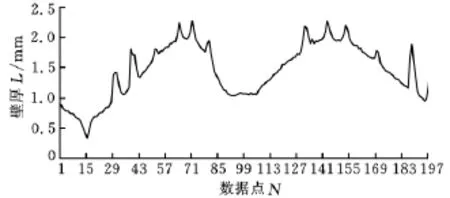
圖9 某復雜空心渦輪葉片截面5壁厚分布圖

從表1的對比結果可知，在后緣位置法線方法誤差較大，中弧線方法比法線方法平均誤差減小了1.077%，綜合比較得出中弧線方法與實際測量結果相對誤差較小，與實際結果一致性較好。

表1 渦輪葉片壁厚計算結果對比表

4 結語

本文介紹了基于CT測量數據的空心渦輪葉片壁厚計算實施過程，提出了一種基于中弧線的空心葉片壁厚計算方法，通過對空心葉片CT切片數據的采集與處理，建立了相應的點云數據測量模型，并與葉片CAD模型進行配準，實現了空心葉片各截面線的提取和處理，進而對壁厚計算進行了詳細介紹。使用本文介紹的壁厚計算方法可以在葉片（主要是葉身）任意橫截面上計算渦輪葉片的壁厚。與傳統方法相比，本文方法在計算范圍、精度和自動化程度方面對提高空心葉片壁厚精度及可靠性具有一定的實用性。

［1］李澤，李由佳.某機高壓渦輪空心葉片超聲波測壁厚［J］.紅旗技術，1997（4）：33－36.

［2］程云勇，張定華，卜昆，等.基于工業CT測量數據的空心渦輪葉片三維壁厚分析［J］.機械強度，2009，31（5）：791－796.

［3］王慶勝，張定華，程云勇.基于ICT切片圖像的航空發動機渦輪葉片壁厚檢測［J］.計算機工程與應用，2005（2）：203－204.

［4］傅健，路宏年，侯濤.基于ICT圖像的航空發動機渦輪葉片壁厚尺寸精密測量方法［J］.航空學報，2006，27（2）：325－330.

［5］程云勇，張定華，毛海鵬，等，一種基于工業CT的航空發動機渦輪葉片生產檢測系統關鍵技術研究［J］.制造技術與機床，2004（1）：27－30.

［6］胡明昊，任明武，楊靜宇.一種快速實用的特征點匹配算法［J］.計算機工程，2004，30（9）：23－27.

［7］劉晶.葉片數字化檢測中的模型配準技術及應用研究［D］.西安：西北工業大學，2006.

［8］徐岳琳.空心渦輪葉片蠟模壁厚光學檢測技術研究［D］.西安：西北工業大學，2011.

［9］Huang M C，Tai C C.The Pre－processing of Data Points for Curve Fitting in Reverse Engineering［J］.Int.J.Adv.Manuf.Technol.，2000，16（9）：635－642.

［10］Li D Z，Campbell J，Li Y Y.Filling System for Investment Cast Ni－base Turbine Blades［J］.Journal of Materials Processing Technology，2004，148（3）：310－316.

［11］白瑀，張定華，任軍學，等.葉片高質量造型方法研究［J］.機械科學與技術，2003（3）：447－449.

［12］王軍偉.葉片類曲面造型中的參數網格優化技術研究［D］.西安：西北工業大學，2003.