大撓度簡(jiǎn)支矩形薄板受熱力磁耦合作用分岔與混沌

王 平，陳蜀梅，王知人2，

(1.燕山大學(xué) 建筑工程與力學(xué)學(xué)院，河北秦皇島 066004;2.中國科學(xué)院 力學(xué)研究所非線性力學(xué)國家重點(diǎn)實(shí)驗(yàn)室，北京 100080;3.燕山大學(xué) 理學(xué)院，河北秦皇島 066004)

彈性物體中耦合場(chǎng)理論的創(chuàng)立與發(fā)展，對(duì)處在高溫、高壓及強(qiáng)電磁場(chǎng)作用下結(jié)構(gòu)元件強(qiáng)度和可靠性分析具有重要意義［1］。隨著電磁結(jié)構(gòu)在高新技術(shù)領(lǐng)域中的應(yīng)用日益增多，針對(duì)工程中許多構(gòu)件工作在溫度變化環(huán)境中，對(duì)電磁耦合熱彈性現(xiàn)象的研究有非常強(qiáng)的工程背景與理論價(jià)值［2-3］。熱彈耦合振動(dòng)以熱彈耦合與振動(dòng)理論為基礎(chǔ)發(fā)展而來的新興研究方向。Trajkorski等［4］分析了給定邊界條件下圓板熱彈耦合振動(dòng)特性。戴宏亮等［5］研究了厚壁圓筒在熱、磁耦合作用下的動(dòng)態(tài)響應(yīng)。樹學(xué)鋒等［6-7］建立圓板橫向熱彈耦合振動(dòng)方程，并對(duì)常厚度及變厚度圓板非線性熱彈性耦合振動(dòng)進(jìn)行分析。Yeh［8］研究大變形簡(jiǎn)支正交異性矩形薄板的熱彈耦合振動(dòng)。

混沌動(dòng)力學(xué)的不斷發(fā)展與完善極大豐富了非線性科學(xué)的研究領(lǐng)域，為許多古老研究課題注入新的活力，為力學(xué)學(xué)科發(fā)展提供新的動(dòng)力。目前，各種形式構(gòu)件熱彈性耦合振動(dòng)的混沌運(yùn)動(dòng)研究，也取得一些成果。韓強(qiáng)等［9］考慮幾何非線性效應(yīng)與溫度效應(yīng)影響，建立橢圓板周期激勵(lì)作用下熱彈耦合的非線性動(dòng)力方程，利用Melnikov函數(shù)法給出系統(tǒng)發(fā)生混沌運(yùn)動(dòng)的臨界條件。吳曉等［10］研究了矩形板非線性熱振動(dòng)分岔。Yeh等［11］對(duì)熱彈耦合矩形板分岔與混沌進(jìn)行研究。李映輝等［12］研究了變溫環(huán)境下粘彈性梁的混沌運(yùn)動(dòng)。

綜上所述，由目前研究成果看，對(duì)非鐵磁類材料大撓度矩形薄板在熱、力、磁耦合共同作用下熱磁性耦合振動(dòng)的混沌運(yùn)動(dòng)研究尚少。因此本文針對(duì)大撓度矩形薄板，考慮溫度場(chǎng)影響，研究在橫向穩(wěn)恒磁場(chǎng)與機(jī)械載荷共同作用下的非線性熱磁彈性耦合振動(dòng)問題。結(jié)果表明，薄板在多場(chǎng)耦合作用下，具有豐富的非線性動(dòng)力行為。通過改變機(jī)械載荷、電磁場(chǎng)及溫度場(chǎng)參數(shù)，可控制系統(tǒng)的振動(dòng)特性。

1 運(yùn)動(dòng)方程

將矩形薄板置于橫向穩(wěn)恒磁場(chǎng)B(0，0，Bz)中，同時(shí)受分布載荷P(0，0，q)作用.在笛卡兒直角坐標(biāo)系oxyz中，oxy為薄板中面，z為法向坐標(biāo)，不考慮極化、磁化影響，將洛侖茲力［2］ρfx，ρfy，ρfz作為質(zhì)動(dòng)力載荷加入板運(yùn)動(dòng)方程，得薄板熱、力、磁耦合運(yùn)動(dòng)方程為:

式中:h為板厚;q為法向機(jī)械載荷分量;Nx，Nxy，Ny;Qx，Qy;Mx，Mxy，My為內(nèi)力分量;θx，θy為角位移分量;ρ為質(zhì)量密度;ρfx，ρfy，ρfz分別為對(duì)應(yīng)x，y，z的洛侖茲力分量;mx，my為洛侖茲力矩。

洛侖茲力與洛侖茲力矩為［2］:

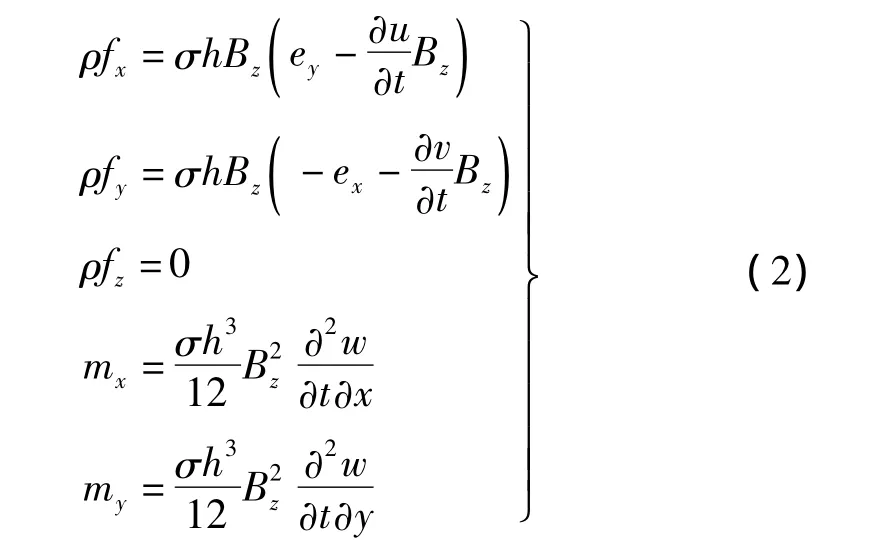
式中:u，v，w分別為中面內(nèi)點(diǎn)x，y，z向位移;t為時(shí)間;σ為電導(dǎo)率;ex，ey為磁感應(yīng)電場(chǎng)強(qiáng)度分量。

矩形板在熱狀態(tài)下的內(nèi)力方程為［13］:

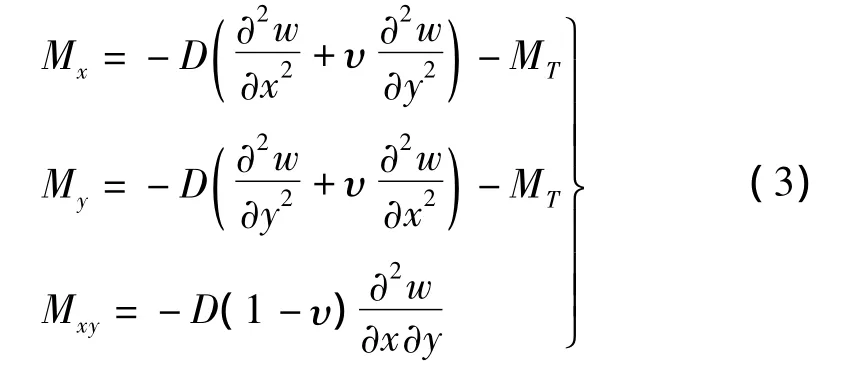
中面內(nèi)力及撓度表示的相容方程為［14］:

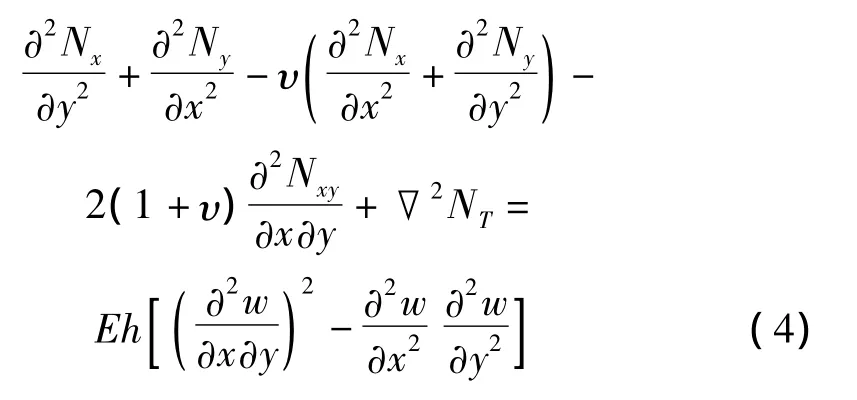
式中:NT為熱力。熱力、熱矩的表達(dá)式為［14］:

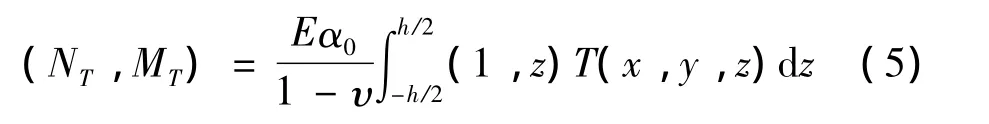
式中:α0為熱膨脹系數(shù)。

引入應(yīng)力函數(shù)φ(x，y):

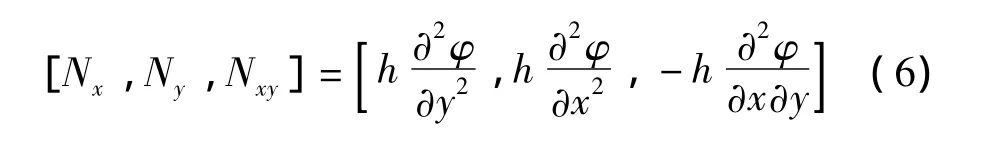
令機(jī)械載荷q=q0cos(ωt)，其中q0為機(jī)械力幅值，ω為激振頻率。式(1)后三個(gè)式子中去掉慣性力項(xiàng)，由式(1)～式(4)及式(6)可得矩形板在熱狀態(tài)下非線性控制方程為:

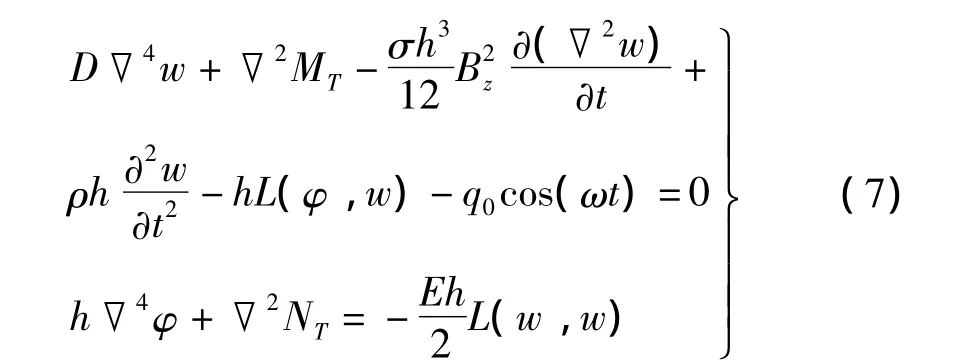
矩形薄板四邊為不可移簡(jiǎn)支，a、b為板邊長(zhǎng)，邊界條件為:

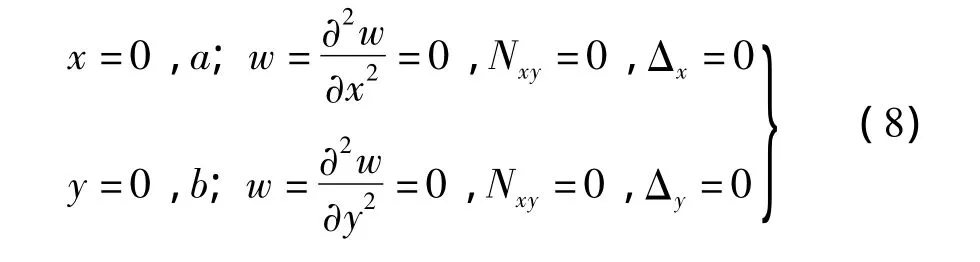
板端部表達(dá)式為:

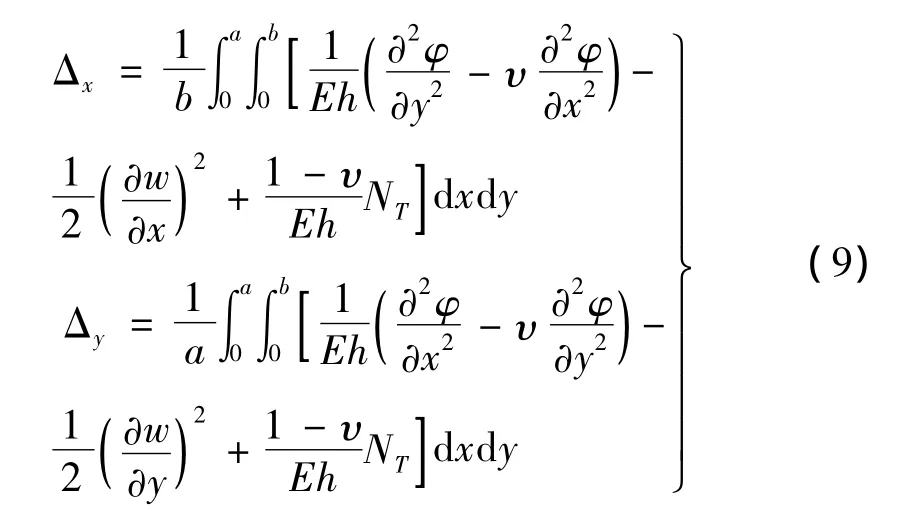
設(shè)溫度函數(shù)為:

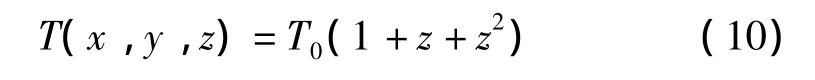
式中:T0為常數(shù)。由于工程實(shí)際中對(duì)最低階振型感興趣，故設(shè):

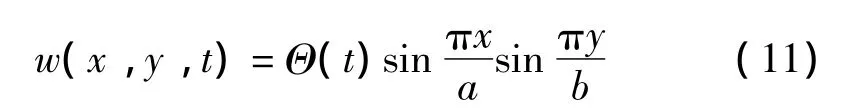
由式(5)、式(7)及式(11)得:

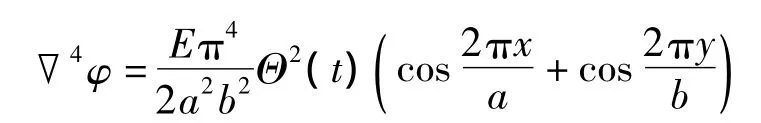
利用待定系數(shù)法［16］，設(shè)應(yīng)力函數(shù)為:

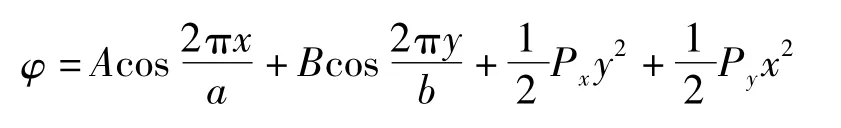
將其代入上式，兩邊比較系數(shù)，得:

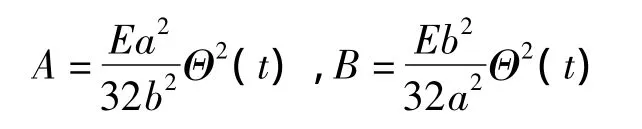
則應(yīng)力函數(shù)為:

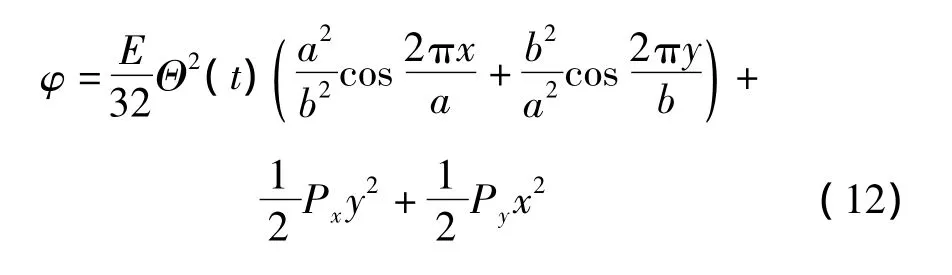
式中:Px，Py由式(9)求得(令:Δx=Δy=0)

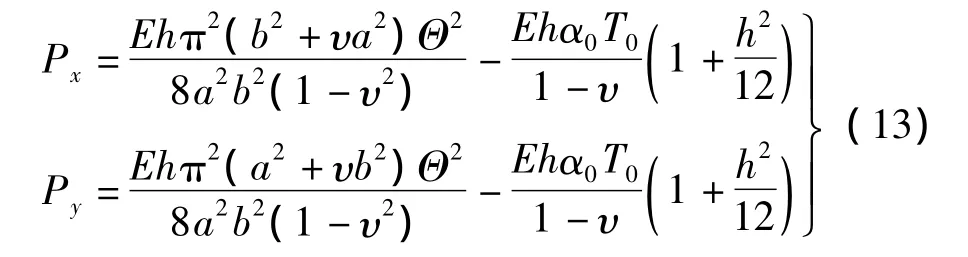
對(duì)式(7)中第一式利用Galerkin原理有:

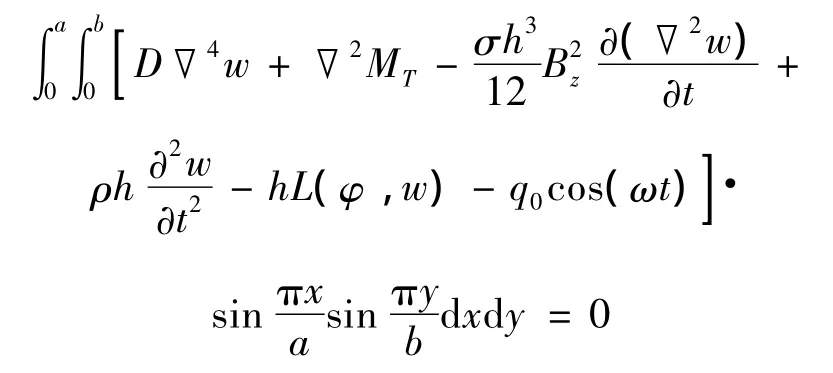
將式(5)、(6)、(11)、(13)代入上式，計(jì)算得:

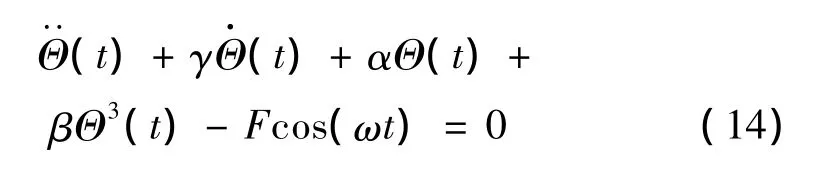
式中:

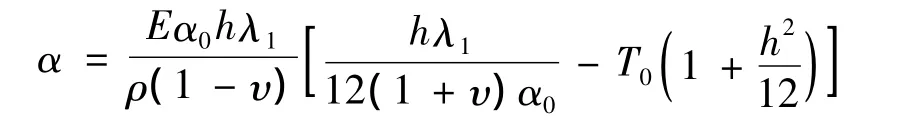
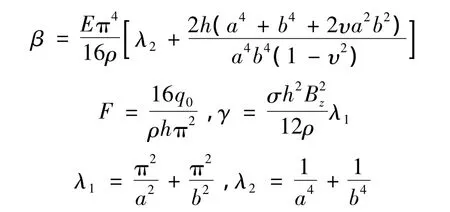
由β表達(dá)式看出β＞0，令η=|α|，則式(14)變?yōu)?

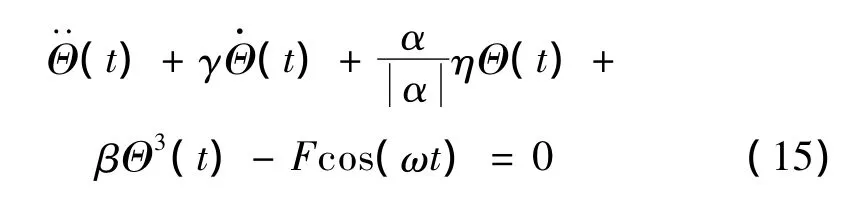
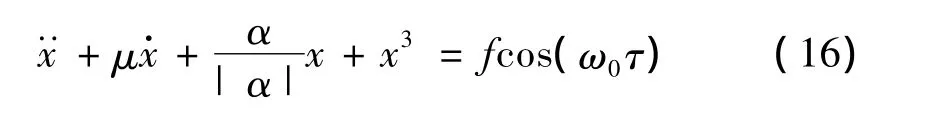
當(dāng)ε=0時(shí)，式(17)為未擾動(dòng)的Hamilton系統(tǒng)，即:

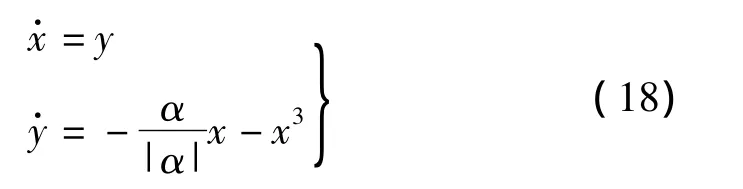
討論α＜0情況，即式(16)為:

當(dāng)α＜0時(shí)，未擾動(dòng)的Hamilton系統(tǒng)有三個(gè)奇點(diǎn)，兩個(gè)鞍點(diǎn)(±1，0)和一個(gè)中心點(diǎn)(0，0)。

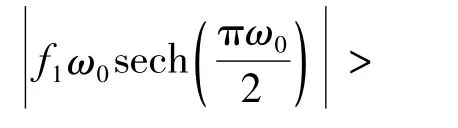
2 數(shù)值解及算例分析

設(shè)薄板為鋁質(zhì)材料。板厚h=2×10-2m，密度ρ=2.67 ×103kg/m3，彈性模量E=71 GPa，泊松比ν=0.34，電導(dǎo)率σ=3.6 ×107(Ωm)-1，熱膨脹系數(shù)α0=23×10-6(℃)-1。為便于計(jì)算，且α＜0，取a=3π m，b=2π m，ω0=1 rad/s。將其代入方程，用四階R-K方法編程求解。計(jì)算中采用積分容忍誤差為10-6。為模擬矩形薄板的混沌運(yùn)動(dòng)，采樣周期為120，在積分所得時(shí)間響應(yīng)中反復(fù)4 000次后開始取資料，以去掉足夠的瞬態(tài)，保證系統(tǒng)動(dòng)態(tài)響應(yīng)已達(dá)到穩(wěn)定狀態(tài)。資料包括位移、加速度、時(shí)間等，用于產(chǎn)生分岔圖、位移波形圖、相平面軌跡圖、及龐伽萊截面圖。

2.1 機(jī)械載荷影響

當(dāng)ω0=1 rad/s，Bz=1 T，T0=20℃時(shí)，通過改變機(jī)械載荷幅值q0大小，使f在0.01～10 N/m2之間變化，得系統(tǒng)隨f變化時(shí)的分岔圖(圖1)。從圖中看出，以機(jī)械載荷f為分岔參數(shù)，隨著機(jī)械載荷幅值q0的不斷增加，系統(tǒng)的混沌與周期區(qū)交替出現(xiàn)。在f=0.2 N/m2附近，系統(tǒng)由周期1運(yùn)動(dòng)經(jīng)由陣發(fā)性進(jìn)入瞬間混沌運(yùn)動(dòng)，轉(zhuǎn)而又開始周期1運(yùn)動(dòng)，當(dāng)f在1～1.6 N/m2之間系統(tǒng)有大面積混沌區(qū)，期間也存在一些零散的周期窗口，f=1.6 N/m2時(shí)系統(tǒng)離開混沌運(yùn)動(dòng)狀態(tài)進(jìn)入周期3運(yùn)動(dòng)，在f=1.8 N/m2附近轉(zhuǎn)而又開始周期6運(yùn)動(dòng)，f在2～2.3 N/m2之間系統(tǒng)處于周期2運(yùn)動(dòng)狀態(tài)，之后進(jìn)入混沌區(qū)，在f=3.1 N/m2附近系統(tǒng)離開混沌進(jìn)入周期1運(yùn)動(dòng)，后經(jīng)由倍周期分岔，在f=4.8 N/m2附近進(jìn)入混沌運(yùn)動(dòng)。后面空白處為周期窗口，之后再次進(jìn)入混沌運(yùn)動(dòng)狀態(tài)，如此反復(fù)。圖2～圖3給出在不同f值下系統(tǒng)位移波形圖、相平面軌跡圖及龐加萊截面圖。當(dāng)f=0.5 N/m2時(shí)，系統(tǒng)處于單周期運(yùn)動(dòng)狀態(tài);f=1.6 N/m2時(shí)，系統(tǒng)處于3周期運(yùn)動(dòng)狀態(tài);f=4.5 N/m2時(shí)，系統(tǒng)處于2周期運(yùn)動(dòng)狀態(tài);f=6.5 N/m2時(shí);系統(tǒng)處于混沌運(yùn)動(dòng)狀態(tài)。

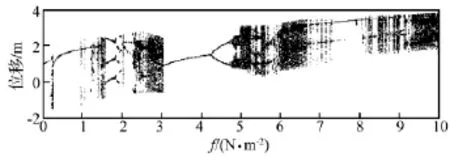
圖1 ω0=1 rad/s，Bz=1 T，T0=20℃時(shí)系統(tǒng)隨f變化時(shí)的分岔圖Fig.1 Bifurcation diagram henf is variable(ω0=1 rad/s，Bz=1 T，T0=20℃時(shí))

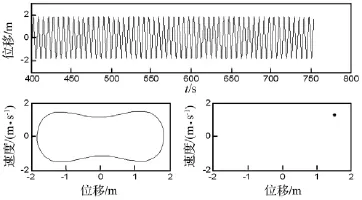
圖2 f=0.5 N/m2時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.2 Wave diagram of displacement，Phase diagram and Poincare map(f=0.5 N/m2)

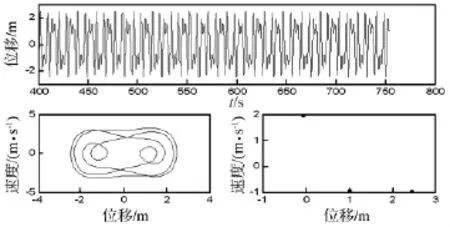
圖3 f=1.6 N/m2時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.3 Wave diagram of displacement，Phase diagram and Poincare map(f=1.6 N/m2)

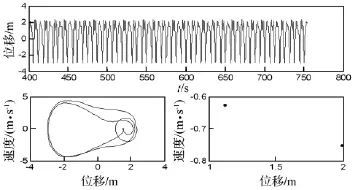
圖4 f=4.5 N/m2時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.4 Wave diagram of displacement，Phase diagram and Poincare map(f=4.5 N/m2)

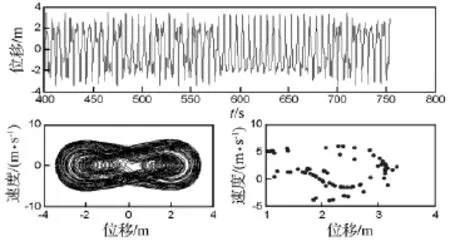
圖5 f=6.5 N/m2時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.5 Wave diagram of displacement，Phase diagram and Poincare map(f=6.5 N/m2)

2.2 電磁場(chǎng)影響

當(dāng)ω0=1 rad/s，T0=20℃，f=1.5 N/m2(q0=0.766 9 N/m2)時(shí)，通過改變磁感應(yīng)強(qiáng)度大小，Bz取0.01～2T，得系統(tǒng)分岔圖如圖6所示。由圖中看出，隨著磁感應(yīng)強(qiáng)度Bz的不斷增加，系統(tǒng)運(yùn)動(dòng)狀態(tài)有較明顯變化。當(dāng)Bz小于0.45T，系統(tǒng)一直處于混沌運(yùn)動(dòng)狀態(tài);在Bz=0.45T附近進(jìn)入3周期運(yùn)動(dòng)狀態(tài);在Bz=0.78T附近離開3周期運(yùn)動(dòng)狀態(tài)進(jìn)入混沌運(yùn)動(dòng)狀態(tài);在Bz=0.78～1.28T范圍內(nèi)，系統(tǒng)基本處于混沌運(yùn)動(dòng)狀態(tài);在Bz=1.2T附近空白處有微小周期窗口;在Bz=1.28～2T范圍內(nèi)系統(tǒng)基本處于單周期運(yùn)動(dòng)狀態(tài);只是在Bz=1.45T左右有短暫的3周期運(yùn)動(dòng)。圖7～圖9為不同Bz值下系統(tǒng)位移波形圖、相平面軌跡圖及龐伽萊截面圖。Bz=0.2T時(shí)，系統(tǒng)處于混沌運(yùn)動(dòng)狀態(tài);Bz=0.6T時(shí)，系統(tǒng)處于3周期運(yùn)動(dòng)狀態(tài);Bz=1.6T時(shí)，系統(tǒng)處于單周期運(yùn)動(dòng)狀態(tài)。

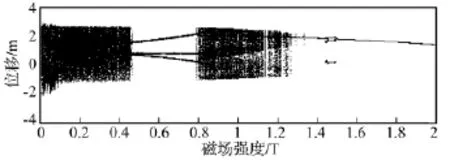
圖 6 ω0=1 rad/s，T0=20℃，f=1.5 N/m2時(shí)系統(tǒng)隨Bz變化時(shí)的分岔圖Fig.6 Bifurcation diagram whenBzis variable(ω0=1 rad/s，T0=20℃，f=1.5 N/m2)

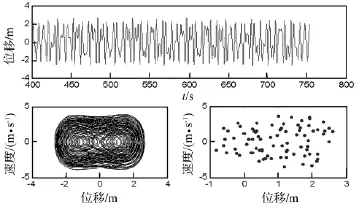
圖7 Bz=0.2T時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.7 Wave diagram of displacement，Phase diagram and Poincare map(Bz=0.2T)

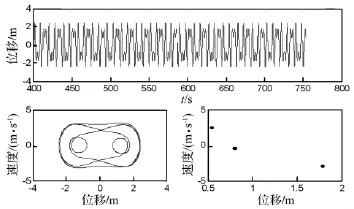
圖8 Bz=0.6T時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.8 Wave diagram of displacement，Phase diagram and Poincare map(Bz=0.6T)

2.3 溫度影響

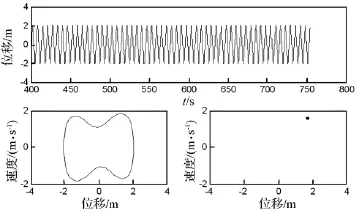
圖9 Bz=1.6T時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.9 Wave diagram of displacement，Phase diagram and Poincare map(Bz=1.6T)

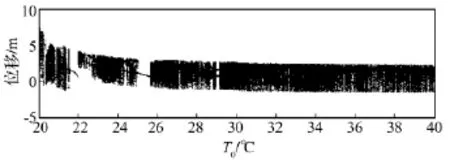
圖10 ω0=1 rad/s，B=1T，q0=70 N/m2時(shí)系統(tǒng)隨T0變化時(shí)的分岔圖Fig.10 Bifurcation diagram whenT0is variable(ω0=1 rad/s，B=1T，q0=70 N/m2)

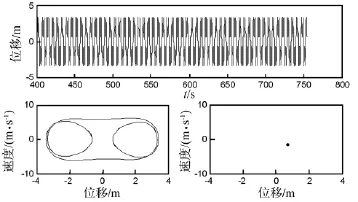
圖11 T0=22℃時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.11 Wave diagram of displacement，Phase diagram and Poincare map(T0=22℃)

當(dāng)ω0=1 rad/s，Bz=1T，q0=70 N/m2時(shí)，通過改變溫度T0的大小(20～40℃)，得系統(tǒng)分岔圖如圖10所示。由圖中看出，系統(tǒng)在T=22℃和T=25℃附近有短暫?jiǎn)沃芷趨^(qū);在T=27℃和T=29℃附近及T=30～40℃范圍內(nèi)的空隙處存在微窄大周期區(qū)。圖11～圖14為在不同溫度T0下系統(tǒng)位移波形圖、相平面軌跡圖及龐伽萊截面圖。T=22℃時(shí)，系統(tǒng)處于單周期運(yùn)動(dòng)狀態(tài);T=27.8℃和T=29℃時(shí)，系統(tǒng)處于大周期運(yùn)動(dòng)狀態(tài);T=35℃時(shí)，系統(tǒng)處于混沌運(yùn)動(dòng)狀態(tài)。

3 結(jié)論

(1)本文用Melnikov函數(shù)法，給出非線性動(dòng)力系統(tǒng)Smale馬蹄變換意義下出現(xiàn)混沌運(yùn)動(dòng)的判據(jù).通過對(duì)系統(tǒng)進(jìn)行數(shù)值模擬，在機(jī)械場(chǎng)、電磁場(chǎng)及溫度場(chǎng)耦合作用下大撓度簡(jiǎn)支矩形薄板系統(tǒng)振動(dòng)方程具有明顯的非線性，運(yùn)動(dòng)特性較復(fù)雜，周期區(qū)與混沌區(qū)交替出現(xiàn)，混沌區(qū)中既有單周期窗口，也有倍周期窗口、大周期窗口，混沌與分岔現(xiàn)象較豐富。

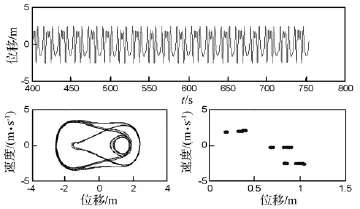
圖12 T0=27.8℃時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.12 Wave diagram of displacement，Phase diagram and Poincare map(T0=27.8℃)

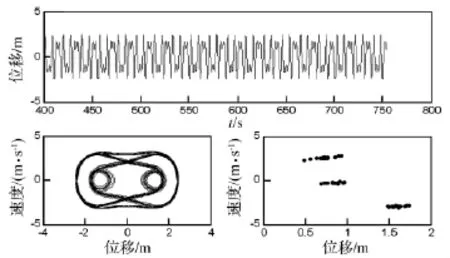
圖13 T0=29℃時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.13 Wave diagram of displacement，Phase diagram and Poincare map(T0=29℃)

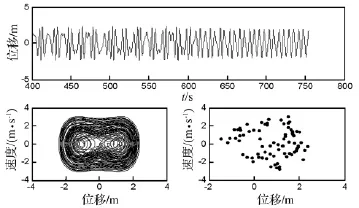
圖14 T0=35℃時(shí)的位移波形圖，相平面軌跡圖及龐加萊截面圖Fig.14 Wave diagram of displacement，Phase diagram and Poincare map(T0=35℃)

(2)單周期或k周期運(yùn)動(dòng)，對(duì)應(yīng)相平面軌跡圖為1條或k條連續(xù)的封閉曲線，在龐加萊截面圖上顯示1個(gè)或k個(gè)點(diǎn)，位移波形具有明顯周期重復(fù)性;混沌運(yùn)動(dòng)，對(duì)應(yīng)的相平面軌跡圖軌線較紊亂，龐加萊截面圖呈云片狀、雜亂無章，位移波形呈類隨機(jī)紊亂狀態(tài)。

(3)通過變化機(jī)械載荷、電磁參數(shù)及溫度可使系統(tǒng)進(jìn)入混沌運(yùn)動(dòng)狀態(tài)，或避免混沌運(yùn)動(dòng)，以實(shí)現(xiàn)對(duì)系統(tǒng)振動(dòng)特性控制。本文研究結(jié)果可作為工程在溫度環(huán)境下電磁結(jié)構(gòu)安全性、可靠性設(shè)計(jì)參考。

［1］周又和，鄭曉靜.電磁固體結(jié)構(gòu)力學(xué)［M］.北京:科學(xué)出版社，1999:1-8.

［2］白象忠.板殼磁彈性力學(xué)基礎(chǔ)［M］.北京:科學(xué)出版社，2006.

［3］ Ghosh M K，Kanoria M.Generalized thermoelastic functionally graded spherically isotropic solid containing a spherical cavity underthermalshock［J］.Applied Mathematics and Mechanics，2008，29(10):1263-1278.

［4］ Trajkovski D，Cukic R.A coupled problem of thermoelastic vibrations of a circular plate with exact boundary conditions［J］.Mechanics Research Communications，1999，26(2):217-224.

［5］戴宏亮，戴慶華.厚壁圓筒在熱磁耦合場(chǎng)作用下的動(dòng)態(tài)響應(yīng)［J］.動(dòng)力學(xué)與控制學(xué)報(bào)，2003，1(1):78-83.

DAI Hong-liang，DAI Qing-hua.The dynamic responses of thick-walled cylinders under the coupling of temperature field and magnetic field［J］.Journal of Dynamics and Control，2003，1(1):78-83.

［6］樹學(xué)峰，張曉晴，張晉香.周邊固支圓板非線性熱彈耦合振動(dòng)分析［J］.應(yīng)用數(shù)學(xué)和力學(xué)，2000，21(6):647-654.

SHU Xue-feng，ZHANG Xiao-qing，ZHANG Jin-xiang.Thermoelastic free vibration of clamped circular plate［J］.Mathematics and Mechanics，2000，21(6):647-654.

［7］李志剛，樹學(xué)鋒.一類變厚度圓板非線性熱彈耦合的振動(dòng)分析［J］.太原理工大學(xué)學(xué)報(bào)，2004，35(1):9-12.

LI Zhi-gang，SHU Xue-feng.Basic theory and method for analysing nonlinear thermoelastic vibration of round plate with variable thickness［J］.Journal of Taiyuan University of Technology，2004，35(1):9-12.

［8］ Yeh Y L.The effect of thermo-mechanical coupling for a simply supported orthotropic rectangular plate on nonlinear dynamics［J］.Thin-Walled Structures，2005，43(8):1277-1295.

［9］韓 強(qiáng)，張年梅，楊桂通.非線性熱彈耦合橢圓板的混沌運(yùn)動(dòng)［J］.應(yīng)用數(shù)學(xué)和力學(xué)，1999，20(9):896-901.

HAN Qiang，ZHANG Nian-mei，YANG Gui-tong.Chaotic motion of a nonlinear thermoelastic elliptic plate［J］.Mathematics and Mechanics，1999，20(9):896-901.

［10］吳 曉，馬建勛.矩形板的非線性熱振動(dòng)分岔［J］.振動(dòng)與沖擊，1999，18(4):55-58，62.

WU Xiao，MA Jian-xun.The nonlinear thermal vibration bifurcation of rectangular plate［J］.Journal of Vibration and Shook，1999，18(4):55-58，62.

［11］ Yeh Y L，Chen C K，Lai H Y.Chaotic and bifurcation dynamics for a simply supported rectangular plate of themomechanical coupling in large deflection［J］.Chaos，Solitons Fractals，2002，13(7):1493-1506.

［12］李映輝，杜長(zhǎng)城，高 慶.變溫環(huán)境下粘彈性梁的混沌運(yùn)動(dòng)［J］.西安交通大學(xué)學(xué)報(bào)，2007，42(6):685-690.

LI Ying-hui，DU Chang-cheng，GAO Qing.Chaotic motion of a viscoelastic beam in time dependent temperature field［J］.Journal of Southwest Jiaotong University，2007，42(6):685-690.

［13］徐芝綸.彈性力學(xué)(上冊(cè)，第三版)［M］.北京:高等教育出版社，1990:55-57，190-194.

［14］吳連元.板殼穩(wěn)定性理論［M］.武漢:華中理工大學(xué)出版社，1996.

［15］高普云.非線性動(dòng)力學(xué):分叉、混沌與孤立子［M］.長(zhǎng)沙:國防科技大學(xué)出版社，2005.