基于遺傳算法的數控噴字路徑優化方法研究＊

周 盛 李 瑞 汪 洋

（武漢理工大學能源與動力學院1） 武漢 430063） （大連理工大學船舶工程學院2） 大連 116024）

（大連中遠船塢工程有限公司3） 大連 116113）

在船體建造過程中，鋼料劃線和切割主要由數控切割機來完成，但是在大多數船廠中，在切割零件上標注零件編號、裝配符號等施工信息時仍由手工完成，效率較低，有的船廠采用數控噴字設備來完成鋼板上零件的噴字標注，相對于人工標注，數控噴字設備的使用提高了噴字效率，但是，零件的噴字順序往往人為給定，容易造成數控噴頭空行路徑過長，因此，為了減少噴頭空走路徑，提高設備的效率，本文根據鋼板上噴字的坐標位置和字符長度，對噴頭行走路徑進行了優化研究．

旅行商問題（traveling salesman problem，TSP）是計算機科學中的一個典型問題［1］，本文將數控噴字路徑優化問題與旅行商問題進行了對比分析，將旅行商問題中節點間路徑的優化擴展為數控噴字路徑中有向線段間路徑的優化，在此基礎上，建立了數控噴字路徑優化數學模型，并采用遺傳算法對其進行了求解．

1 問題描述與分析

1.1 TSP問題描述［2－3］

旅行商路徑問題可描述為：已知n個城市各城市間的距離，某一旅行商從某個城市出發訪問每個城市一次且僅一次，最后回到出發城市，怎樣安排才使其所走路線最短．

其數學模型為：對于城市ti的一個訪問順序為T＝（t1，t2，…，tn），則旅行商問題為求商人所行的最短路徑，即為

式中：Ω為n個城市不重復排列的所有可能的回路．因此，旅行商問題實際上即是給定的一組離散點，求不重復連接所有離散點的最短路徑．

1.2 數控噴字路徑數學模型

數控噴字路徑優化與旅行商問題類似，可以抽象為求不重復連接所有字符串的最短路徑，二者的區別是旅行商問題是基于一組離散點，每個離散點的特征屬性僅是點坐標；數控噴字路徑優化問題是基于一組字符串，每個字符串的特征屬性根據數控噴字的指令文件有起始點坐標、字符串與X軸角度和字符串長度，因此，可以將每個字符串看成是一條有向線段，數控噴字路徑優化問題再次抽象為求不重復連接所有有向線段的最短路徑，見圖1a）是給定的一組有向線段，見圖1b）是這一組有向線段的路徑圖．數控噴字路徑的優化就是確定這組有向線段的順序，使得噴頭按這一順序所行的空行路徑最短．

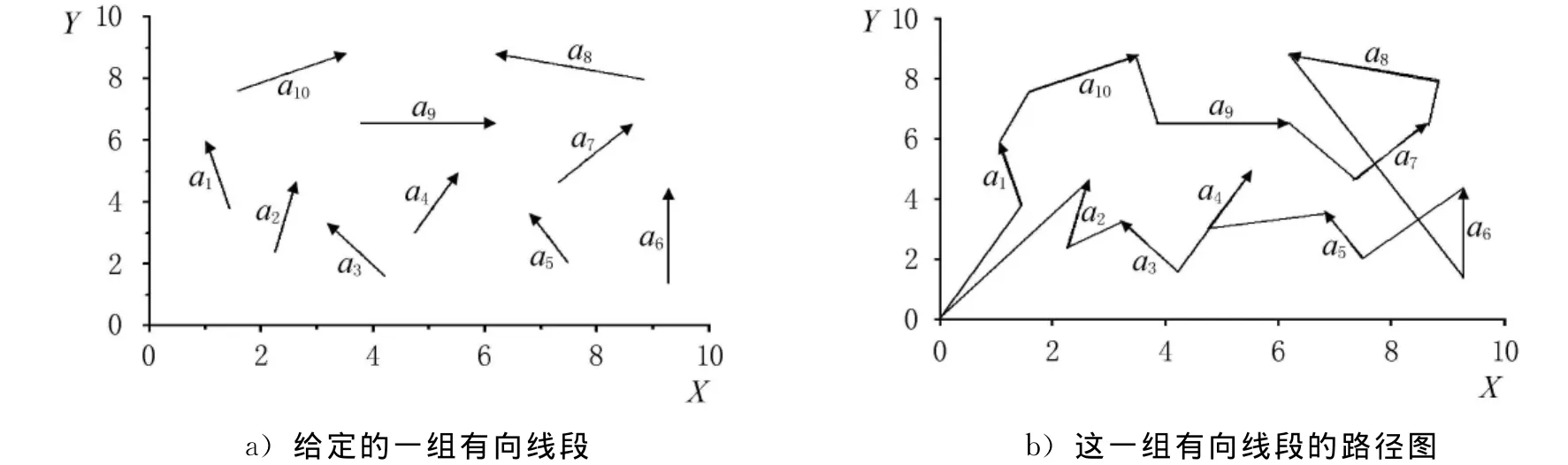
圖1 噴字路徑示意圖

1.3 噴字路徑優化分析

根據上述對數控噴字路徑優化問題的描述及其數學模型的建立，從中可以發現其問題的求解思路、方法與求解TSP問題有相似之處．通過把數控噴字優化問題與TSP問題進行對比分析可知，它們都是一個如何合理安排路徑的問題，所以可以把噴字路徑優化問題歸結為特殊的TSP問題進行求解．

數控噴字路徑優化在TSP問題下可以描述為：對于一組待噴字符段，數控噴頭首先從原點（未啟動的停放位置）開始，在工作臺平面上沿著使總空行路徑最短的軌跡，空走移動到待噴字符段的起始點上，然后按照數控程序指令進行噴字，噴完該段標注字符后，再移動到其他的噴字字符段重復該噴字過程．直到所有噴字字符段都噴完，然后噴頭回到原點位置．

因此，可以根據每個字符串的起始點坐標、與X軸的角度和字符串長度，求出每個字符串的終點坐標，這樣，就可以將數控噴字路徑優化問題轉化為一一對應的一組起始點和終點的TSP問題，增加約束條件為：數控噴頭行走到一個起始點后，下一步只能行走到與其對應的終點位置，再下一步的路徑，只能以剩下的起始點為目標，以此類推．優化目標即是使數控噴頭的空行程最短．

2 遺傳算法求解特殊TSP問題

遺傳算法是一種搜索最優解的方法［4－6］，該方法是通過模擬生物進化過程實現的．遺傳算法以群體中的所有個體為對象，對解空間的每一個個體進行編碼，通過遺傳操作選擇、交叉、變異等迭代從解空間尋找含有最優解或較優解的組合．在進行個體優劣的判斷時，利用由目標函數構造的適應度函數來進行判斷．通過對每一代群體都進行遺傳迭代操作，那么解空間中的解就向最優解逼近，到遺傳算法終止，則所得可行解即為最接近最優解的解．

1）編碼 本文使用路徑順序表達形式．這種表達方法是TSP問題的最自然、最簡單的表示方法．例如：對于一個有9個噴字字符段的的待加工零件，其噴字順序為1－3－2－5－4－7－6－9－8可簡單表示為［1 3 2 5 4 7 6 9 8］，表示從1號字符段出發依次經過3，2，5，4，7，6，9，8字符段最后返回1號字符段的一條路徑．并且這種表達方式滿足TSP問題的約束條件．保證了每個字符段經過且只經過一次．

2）生成初始群體 種群規模越大，種群的多樣性越好，算法越容易跳出局部最優．但隨著種群規模的增大，計算量增大，算法易產生早熟，一般都是隨機生成規模為N的初始群體，N的值取為20～200．

3）適應度函數 對于求解最小值問題，采用如下變換

式中：cmax為一個適當大的數．cmax取為群體中最差個體的路徑長度，就相當于差個體淘汰制．

4）確定交叉算子 目前己有多種交叉算子，如部分映射交叉算子，序交叉算子、循環交叉算子，其中啟發式交叉和邊重組交叉相對有效．本文選用啟發式交叉算子．

3 數控噴字路徑優化實例

應用Matlab編寫基于遺傳算法的數控噴字路徑優化程序，以某塊船體外板上30個噴字字符段為例，首先確定以下參數如下：種群大小N＝30；最大進化代數T＝100；交叉概率Pc＝0．65；變異概率Pm＝0．01；賭輪盤選擇算子；啟發式交叉算子；變異算子．

經過遺傳算法50代后的結果就得到了較大的改進，已開始在接近最優近似解．在60代之后兩代中最好解之間的誤差不超過5%，為了在更短的時間內得到較滿意的解，即可在60代時終止遺傳進化．這在連續處理較多數量鋼板的噴字路徑優化時，時間上的優勢會比較明顯．

對于未集成路徑優化算法的噴字設備，其原始噴字路徑圖見圖2，圖3是采用遺傳算法路徑優化計算結果的路徑圖．優化后空行路徑比未優化的路徑減少了22%．

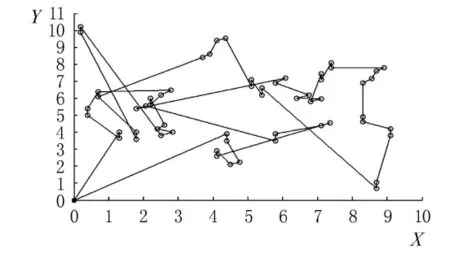
圖2 原始路徑圖

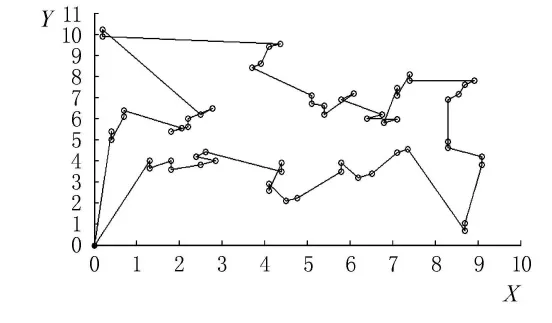
圖3 遺傳算法優化后路徑圖

4 結束語

將數控噴字路徑優化問題與計算科學中經典的TSP問題進行了對比分析，根據噴字特征，將噴字字符串抽象為有向線段，因此，將數控噴字路徑優化問題抽象為一一對應的一組起始點和終點的特殊的TSP問題，建立了數控噴字路徑優化的有向線段路徑優化模型，以噴字空行路徑最短為目標，利用遺傳算法進行了求解．

通過實例計算結果表明，基于遺傳算法的數控噴字路徑優化方法，能夠大幅減少數控噴頭的空行路徑，由此提高數控噴字設備的加工效率．

［1］邢文訓，謝金星．現代優化計算方法［M］．北京：清華大學出版社，1999．

［2］ALBERTO G，RICARDO G．A particale swarm－based met heuristic to solve the traveling salesman problem［C］／／Procedings of the 2006International Conference on Artificial Intelligence，2006：698－702．

［3］HANG，NA S．A study on torch path planning in laser cutting process，part 2：cutting path optimization using simulated annealing［J］．Journal of Manufacturing Process，1999（1）：62－70．

［4］孫惠文．遺傳算法求解旅行商問題［J］．西南交通大學學報，1996，31（5）：550－554．

［5］喻 菡．遺傳算法求解TSP的研究［D］．成都：西南交通大學，2006．

［6］GREFENSTETTE J，COPAL R，ROSIMAITA B．Genetic algorithms for the traveling salesman problem［C］／／Proc Int Genetic Algorithms and Their Applications Conference，1985：160－168．