預應力超高強混凝土梁彈性剛度分析＊

（大連理工大學港口和近海工程國家重點實驗室 大連 116024）

0 引 言

隨著橋梁工程技術的不斷發展，大跨度、超高強裝配式后張法預應力混凝土橋梁被廣泛應用于公路工程建設項目中［1］，但是我國新頒布的規范《公路鋼筋混凝土及預應力混凝土橋涵設計規范》（JTG D62－2004）適應的混凝土強度等級為C15～C80［2］，然而隨著混凝土技術的發展，比規范混凝土強度等級更高的超高強混凝土在實際工程中已逐漸得到應用及推廣．在應用超高強混凝土時，現行混凝土橋涵設計規范規定的彈性剛度折減系數是否適用或需要修訂是一個迫切需要研究卻一直未得到有效解決的問題．因此，可通過對預應力超高強混凝土梁的試驗研究，對其彈性剛度進行詳細分析．

混凝土應變的觀測，由于張拉端錨具變形和預應力筋內縮損失導致預應力的衰減，對有效預加應力產生重大影響，因此張拉過程中在試驗梁的受壓區粘貼混凝土應變片，以監測張拉過程中混凝應變的變化，并根據材料力學公式，求得有效預加應力；反拱值測量，在張拉工程中，對試驗梁進行變形測量，并結合有效預加應力和材料力學理論，尋求反拱值與剛度之間的變化關系．

1 試驗基本情況

試驗共對9根后張法預應力超高強混凝土簡支梁進行張拉階段的受力監測，截面尺寸為160 mm×340mm，混凝土標號為C100，彈性模量為5．28×104N／mm2，普通縱向受力鋼筋采用HRB335級鋼筋，箍筋為HPB235級鋼筋，彈性模量為2．1×105N／mm2，預應力筋采用1860級鋼絞線，彈性模量為1．95×105N／mm2，張拉控制應力均為0．75fptk（fptk為預應力筋抗拉強度標準值），直徑分別為15．2mm和12．7mm，預應力錨具采用低回縮錨具，梁長L＝1．2，1．4，1．6m．梁的截面尺寸見圖1，低回縮錨具見圖2，配筋情況見表1．

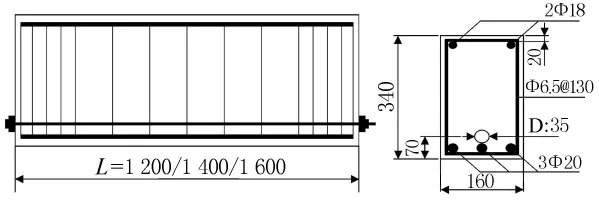
圖1 試驗梁的配筋圖（單位：mm）

在張拉過程中用標距為100mm的混凝土應變片測試受壓區的混凝土應變，并分別在梁的兩端以及中間安裝LVDT，設兩端讀數分別為a和b，中間的讀數為c，見圖3，那么反拱值計算式為f＝c－（a＋b）／2，利用IMC數據采集儀采集混凝土應變和反拱值．

圖2 低回縮錨具

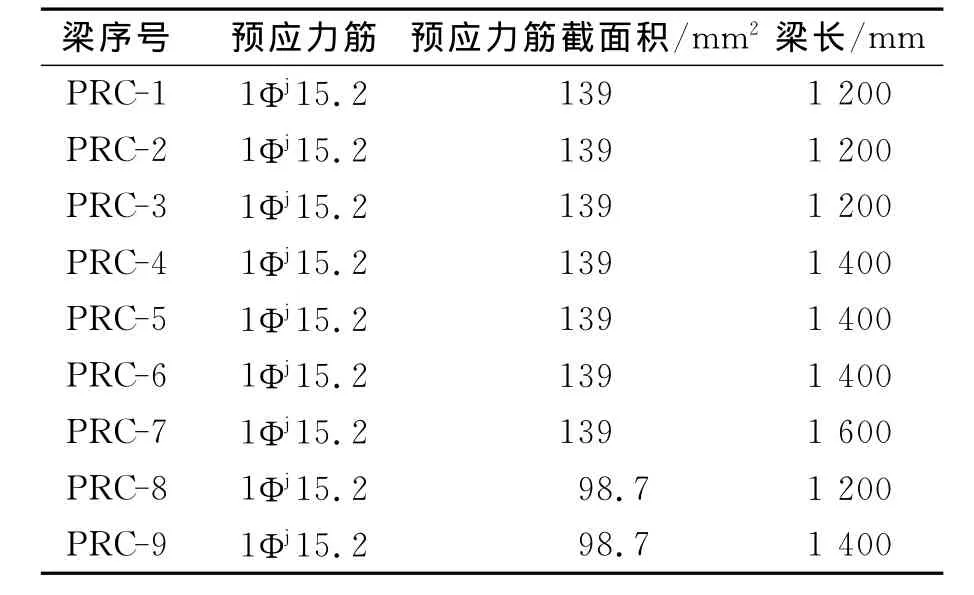
表1 試驗梁的設計參數

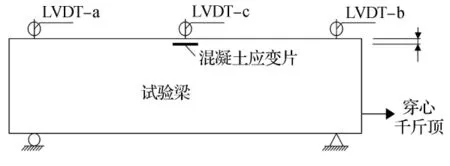
圖3 試驗梁測點圖

2 預應力超高強混凝土梁剛度分析

根據文獻［3］，影響構件截面剛度的彎矩分為2部分，即M＝M0＋M1．式中：M0為有效預加應力產生的彎矩；M1為試驗梁自重產生的彎矩．由于試驗梁的自重較小，可以忽略不計，因此：M＝M0．

2.1 有效預加應力的計算

根據測試得到的混凝土受壓區應變值，可獲得預應力超高強混凝土梁的有效預加應力為［4］

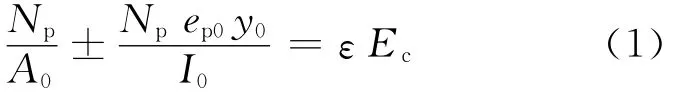
式中：Np為預應力超高強混凝土梁的有效預加應力；A0為試驗梁換算截面面積；I0為試驗梁換算截面慣性矩；ep0為換算截面重心至預加力作用點的距離；y0為換算截面重心至所計算纖維處的距離；ε為計算纖維處混凝土的應變值；Ec為混凝土的彈性模量．

2.2 剛度折減系數計算

由于Np是考慮第一批預應力損失的預應力鋼筋合力，因此試驗梁在施加預應力后，在不考慮梁體自重的情況下，得出作用在預應力超高強混凝土梁上的彎矩為［5］

預應力超高強混凝土梁反拱值為

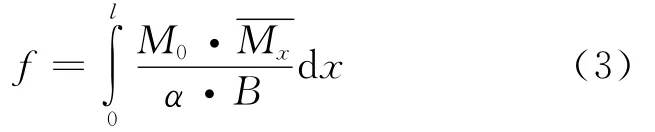
式中：α為彈性剛度折減系數；Mx為跨中作用單位力時任意截面處所產生的彎矩值；B＝EcI0．

將式（1），（2）代入式（3）得

3 剛度折減系數的計算

本次試驗梁的預應力采用兩次張拉的方法，首次張拉預應力為1．05σp（σp＝0．75fptk），然后逐漸放張，再次張拉到1．05σp時，擰緊低回縮錨具的螺環．同時監測兩次張拉后試驗梁的反拱值和混凝土應變．并將混凝土應變值代入式（1）中，求出預應力筋的有效預加應力，將有效預加應力轉換為等效荷載，并將梁體的反拱值和等效荷載產生的彎矩代入式（4）中便可求得梁體彈性剛度的折減系數．計算結果見表2．

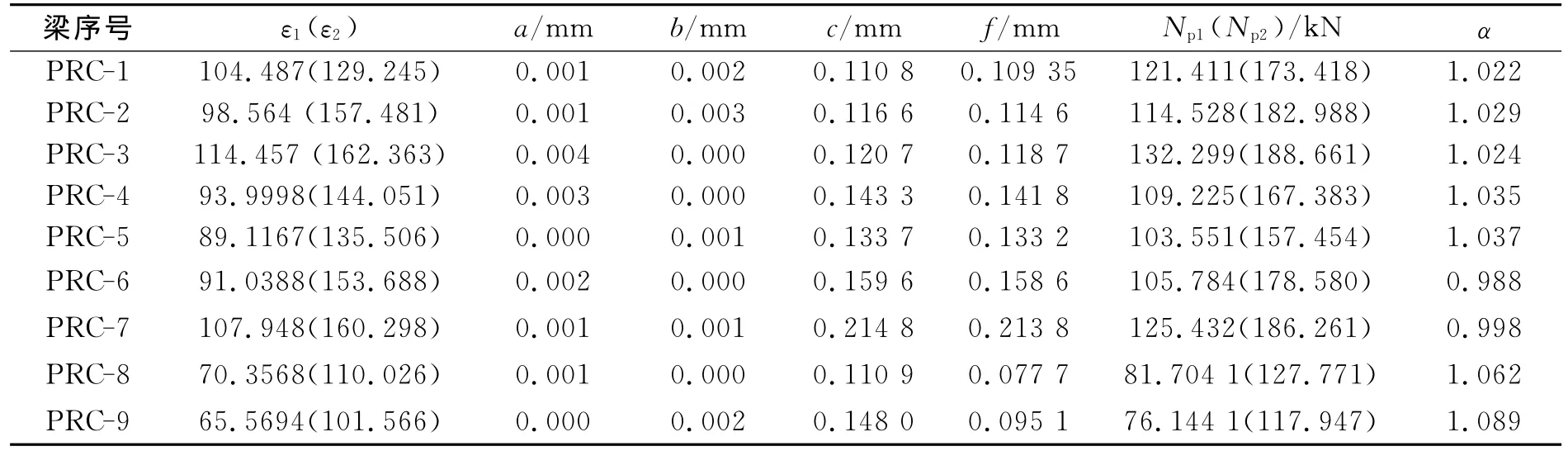
表2 彈性剛度折減系數計算結果

由表2可見，第二次張拉后的預加應力均大于第一次張拉后的預加應力，增幅為42．6%～68．8%，說明采用低回縮錨具能夠有效降低由于張拉端錨具變形和鋼筋內縮導致的預應力損失．本文試驗得到的預應力超高強混凝土梁的彈性剛度折減系數為0．998～1．089，而文獻［6］根據全預應力混凝土梁的試驗結果得到的彈性剛度折減系數在0．91～1．06之間，通過對比可以看出，本文試驗得到的彈性剛度折減系數略大于文獻［6］的試驗值，這主要是因為本文試驗梁所采用的超高強混凝土的彈性模量顯著大于普通混凝土的彈性模量，本文得到的試驗梁的彈性剛度折減系數平均值ˉX＝1．031 556，若取保證率為95%，則有

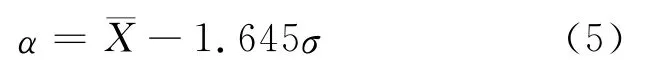
式中：α為彈性剛度折減系數；ˉX為試驗梁的彈性剛度折減系數平均值；σ為標準差．根據式（5）計算可以得到預應力超高強混凝土梁的彈性剛度折減系數α為0．98．

4 結 論

1）采用低回縮錨具可以有效降低由于張拉端錨具變形和鋼筋內縮導致的預應力損失．

2）根據現在理論推導出預應力超高強混凝土梁的剛度折減系數計算公式，并根據預應力超高強混凝土梁在張拉階段的跨中反拱值與混凝土應變的試驗結果，對預應力超高強混凝土梁的彈性剛度進行理論分析．

3）指出影響預應力超高強混凝土梁剛度折減系數的因素，并給出了預應力超高強混凝土梁基于概率論的彈性剛度折減系數建議值，該值為0．98，為工程應用提供了依據，為混凝土和公路橋涵等規范提供了補充．

［1］張謝東，林 清，楊吉新，等．預應力混凝土梁上拱度試驗研究［J］．武漢理工大學學報：交通科學與工程版，2003，25（6）：322－325．

［2］中交公路規劃設計院．JTG D62－2004公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］．北京：人民交通出版社，2004．

［3］葉見曙．結構設計原理［M］．2版．北京：人民交通出版社，2005．

［4］林同炎．預應力混凝土結構設計［M］．3版．北京：中國鐵道出版社，1993．

［5］中交公路規劃設計院．GB50152－92混凝土結構試驗方法標準［S］．北京：人民交通出版社，1992．

［6］張克波．靜載和疲勞荷載作用下PPC受彎構件的撓度［J］．長沙交通學院學報，1990，12（4）：59－68．