基于擁堵控制的軸輻式海運網絡樞紐港選擇模型

林天倚， 盧春霞

(上海交通大學 船舶海洋與建筑工程學院，上海 200240)

0 引 言

當前,世界主要集裝箱港口間已初步形成軸輻式海運網絡格局.軸輻式網絡通過集中流量產生規模經濟效應以降低單位運輸成本，但正是由于對規模效應的追求造成大量貨流集中于樞紐港，使軸輻式網絡較一般網絡更有可能造成節點擁堵.與此同時，港口擁堵是長期困擾班輪運輸業的一大難題，嚴重的擁堵迫使航次時間增加并可能引發一系列連鎖反應，對整個集裝箱海運系統造成嚴重的經濟損失，所以在進行網絡布局研究的同時必須考慮擁堵因素.

O’KELLY[1]最早研究物流系統的P樞紐中位問題，將其歸結于一個二次規劃模型并求解.隨后AYKIN[2]和ERNST等[3]將此類問題進一步歸結為NP模型，鑒于傳統方法求解此類問題有一定難度，嘗試應用隨機速降等啟發式算法求解并取得良好效果.

此后的研究使得模型的假設更加符合實際情況.YAMAN等[4]提出用“模塊化容量”的思路解決單分配軸輻式通信網絡的設計問題，樞紐節點間的容量限制以非線性的方式被逐步處理.EBERY等[5]考慮一個空運網絡中樞紐港間貨流容量的問題.da GRA?A COSTA等[6]展示一種用于單分配有容量限制的軸輻式網絡選擇問題的多目標方程.除了以成本最小作為目標函數以外，他們還考慮樞紐港處理貨量的最長時間的最小值.李莉等[7]通過添加時間約束對軸輻式快遞網絡進行研究.

另一方面，關于緩解港口擁堵的研究主要集中在分析擁堵產生的原因和優化集疏運體系等方面.陳淑文[8]和壽建敏[9]分別對港口擁堵的背景、擁堵特征和原因等進行分析，并對世界海運和多式聯運格局的潛在影響進行論述，同時提出可能出現的排解港口擁堵的方法.FAN等[10]建立一個多式聯運網絡，對美國進口集裝箱運輸網絡的空間競爭性、擁堵狀況及貨流進行研究.LEACHMAN等[11]通過排隊理論建立基于進口貨量、操作人員和裝備能力的“貨流-時間”模型，用以預測通過特定樞紐港的貨量與擁堵時間之間的關系，并且以中國至美國間的集裝箱水路運輸為例對模型進行檢驗.CHEN等[12]利用船舶時間窗口的概念處理口岸集卡擁堵問題，采用“削峰填谷”的思路有效緩解碼頭集裝箱卡車的擁堵.MENG等[13]研究一個軸輻式多式聯運網絡的設計問題，其數學模型考慮多方利益相關者及多種集裝箱的情況，并且采用混合遺傳算法得出結果.靳志宏等[14]針對港口及腹地多式聯運統籌安排的復雜性，通過分析多式聯運計劃的層次，提出多式聯運的分級優化概念，并且針對海上班輪運輸計劃和內陸集疏運計劃建立任務分配的優化模型.白治江[15]以集裝箱船在港時間最少為目標，采用層次分解技術研究集裝箱堆場的資源分配問題.

綜上所述，軸輻式網絡模型的研究主要涉及對數學模型的完善和提高算法效率這兩個方面.在實證案例中多應用于物流、航空運輸、地面交通等領域，在海運特別是集裝箱海運方面為數甚少.而在國內，與海運相關的軸輻式網絡研究仍然處于起步階段.在緩解港口擁堵方面，現有的關于港口碼頭擁堵的研究主要涉及對擁堵產生的原因、背景及特征進行定性分析，對衡量擁堵造成的損失和影響缺乏定量判斷的依據.同時，大量的研究成果著眼于通過提高碼頭作業效率、優化集疏運體系等方式緩解單個港口的擁堵情況，未從系統的高度審視整個港口網絡格局對單個港口擁堵造成的影響.本文將擁堵控制與軸輻式網絡設計相結合，以文獻[1]中的軸輻式模型為基礎，在構造海運網絡的同時引入擁堵成本函數.

1 擁堵成本的量化

軸輻式網絡將運輸網絡中的多個節點設立為樞紐，非樞紐節點都經由樞紐彼此相連.雖然軸輻式網絡可以形成規模經濟效應，但這也意味著大量的貨流被集中于樞紐節點，當進入樞紐的貨量超過其最大處理能力時就會形成節點擁堵.擁堵成本的量化就是對擁堵發生時的額外經濟成本進行數學上的表達，該成本可以借由擁堵成本函數描述.

建立擁堵成本函數的假設如下：(1)若港口泊位數為n，則進港船舶均勻地排在n條相鄰的航道上等待接受服務；(2)擁堵成本只發生在樞紐港，且無論樞紐港單日貨物流量多少，總量上擁堵成本一直發生；(3)擁堵成本包含因港口擁堵造成的船公司直接營運損失及其他各類隱性成本.由擁堵造成的船舶單位時間的經濟損失為定值.

首先將正在減速入港的前船視作一個移動的服務臺(平均速度為v1)，則后船以v2-v1的速度到達隊列接受服務.假設航道上船舶的到達率為λ′，則后續船舶追上前船的到達率

根據間隙理論，后船的服務時間不但受本航道船舶的影響，還受相鄰航道船舶到達分布及流量的影響，其改變航道的平均等待時間

式中：Q為相鄰航道流量;τ為臨界間隔常數;μ為平均服務率.

后船受前船影響的平均時間

定義船舶運行延誤為船舶受阻運行時間與理想運行時間之差，前船因港口擁堵對后船造成的平均延誤時間

在不同流量下船舶航行速度之間的關系可以通過BPR路阻函數表示，因此

式中:V(q)表示當交通量為q時航路上的船舶速度;v0表示零流量航路上的船舶速度;K和c表示航路的實際通行能力;α和β是道路阻滯系數.

將某一港口掛靠的所有m條班輪航線加總，每條航線上班輪的間隔為Ii，單位時間內到達的船舶數為λ.將上述各式代入

得到T時間內港口擁堵所造成的船舶總延誤.

通過解析D的表達式可以發現，延誤時間隨流量的增加呈指數遞增關系.由于上式展開后在形式上不利于計算，本文以具有同樣性質的指數函數代替原總延誤函數D[16-18].

因擁堵成本與船舶延誤時間成正比關系，故定義描述擁堵成本與節點流量之間的擁堵成本函數

f(u)=aub

式中:f(u)表示擁堵成本，美元/TEU；u表示某樞紐港的貨量(由于采用指數形式表達，為使函數在整體量綱上統一，計算時將u視為無量綱值，僅保留數值關系)；a為有量綱系數，單位同f(u)；b為正常數且b≥1.參數a=1,b取不同值時的擁堵成本函數見圖1.

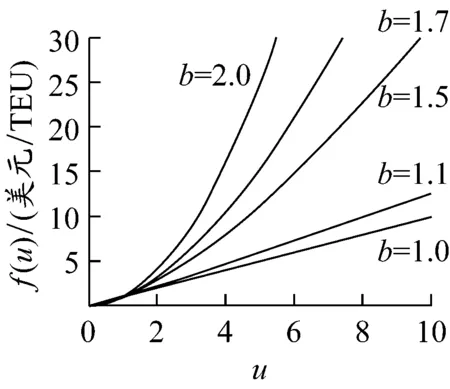
圖1 不同參數下的擁堵成本函數(a=1)

2 模 型

2.1 模型的目標與假設

建立模型的目標是在保證港口間貨物運量的前提下使擁堵成本成為廣義運輸成本的一部分，并使廣義運輸成本最小.模型假設如下：(1)各港口之間的航道沒有通行能力限制；(2)一個非樞紐港既可以只分配給一個樞紐港，也可被分配到多個樞紐港，本文只考慮較為簡單的單分配問題；(3)非樞紐港港口間不可直接連通，所有貨流均需經過樞紐港中轉且至多經過2個樞紐港.

2.2 模型的建立

為描述一個軸輻式海運網絡樞紐港選擇問題，引入如下符號：

G為網絡中港口的集合，節點i,j,k,m∈G.i和j分別表示貨物的起始港和目的港，k和m分別表示貨物運輸途中經過的待定樞紐港.p(p∈N)為待定樞紐港的數量.Fijkm表示以i為起始港、j為目的港，且依次通過i,k,m,j的貨物運輸成本，其計算式為

Fijkm=Wij×(Cik+αCkm+Cmj)

式中:Wij表示從i到j的貨物需求量;Cik,Cmj,Ckm分別表示貨物從i到k、從m到j以及k與m之間的單位運輸成本;α表示樞紐港間運輸的規模經濟效應折扣.記0-1決策變量Zik,Zkk及Xijkm，其意義分別為：Zik取1表示節點i被分配到樞紐港k，取0則表示未被分配到樞紐港k；Zkk取1表示節點k被選為樞紐港，取0則表示未被選為樞紐港；Xijkm取1表示從i到j的貨流經過k和m，且依次通過i,k,m,j.

結合第1節引入的擁堵成本函數，建立數學模型：

(1)

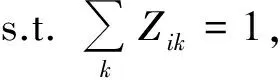
(2)

Zik≤Zkk, ?i,k∈G

(3)

(4)

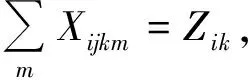
(5)

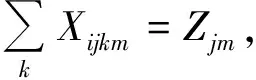
(6)

Xijkm∈{0,1}, ?i,j(>i),k,m∈G

(7)

Zik∈{0,1}, ?i,j(>i),k,m∈G

(8)

目標函數(1)表示網絡內貨物運輸的廣義總成本最小，包括貨物運輸成本及樞紐港擁堵成本；式(2)保證對網絡中的任意節點i只能被唯一地分配到某個樞紐港；式(3)表示只有在港口k被確定為樞紐港以后才對其他節點進行分配；式(4)保證樞紐港的數量；式(5)和(6)確保對任意流經(k,m)的貨流，節點i和j被分別分配至節點k和m；式(7)和(8)表示決策變量為0-1變量.

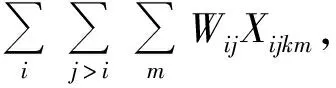
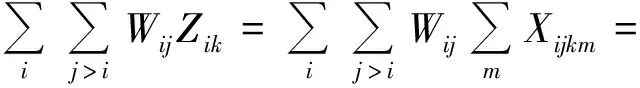
所以原模型可以改寫為

約束條件仍為式(2)～(8).

2.3 目標函數的線性化

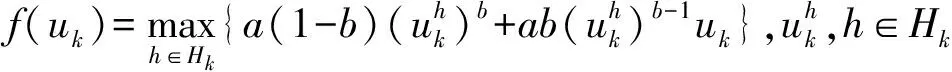
經線性化處理后，原模型可以寫為

約束條件仍為式(2)～(8).

由于在線性化的同時引入無數個約束變量，為保持問題的等價性，模型改寫為

約束條件為式(2)～(8)及

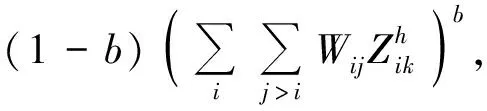
2.4 拉格朗日松弛

將約束條件中的式(2)，(5)，(6)分別用拉格朗日乘子σ，β，γ吸收到目標函數中，有

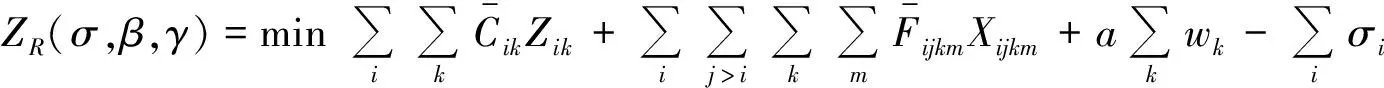
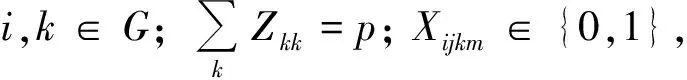
式中:

為方便求解，將原模型分解為以下兩個子問題依次計算：

[子問題1]

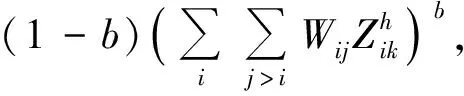
Zik≤Zkk, ?i,k∈G

Zik∈{0,1}, ?i,k∈G

[子問題2]

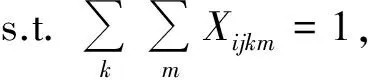
Xijkm∈{0,1}, ?i,j(>i),k,m∈G

3 算法設計

拉格朗日松弛算法的基本思路是將問題中難以求解的約束吸收到目標函數中，并且使原有的目標函數仍然維持線性，在保持前后問題同解的前提下降低原有問題的難度，然后通過循環迭代構造一個啟發式算法逐步逼近取得最優解.因為計算過程在得到解的同時也可得到解的上下界，所以算法在求出目標解的同時也可以用來對解進行評價.針對文中模型設計拉格朗日松弛算法，提供一種求解非線性軸輻式網絡的啟發式算法.算法流程見圖2.具體步驟如下.

步驟1初始化.為變量賦予初始值，包括循環迭代的最大步數N,停止迭代的評判標準ε,搜尋步幅計數變量M及步幅Δ.

步驟2求解子問題1.細分為更小的子問題1-k.采用割平面法先賦予目標函數一組有限個數的約束，再逐一將后續約束添加到先前的約束中直到滿足迭代的停止標準.最后將p個有最小值的Zik對應的函數值相加.

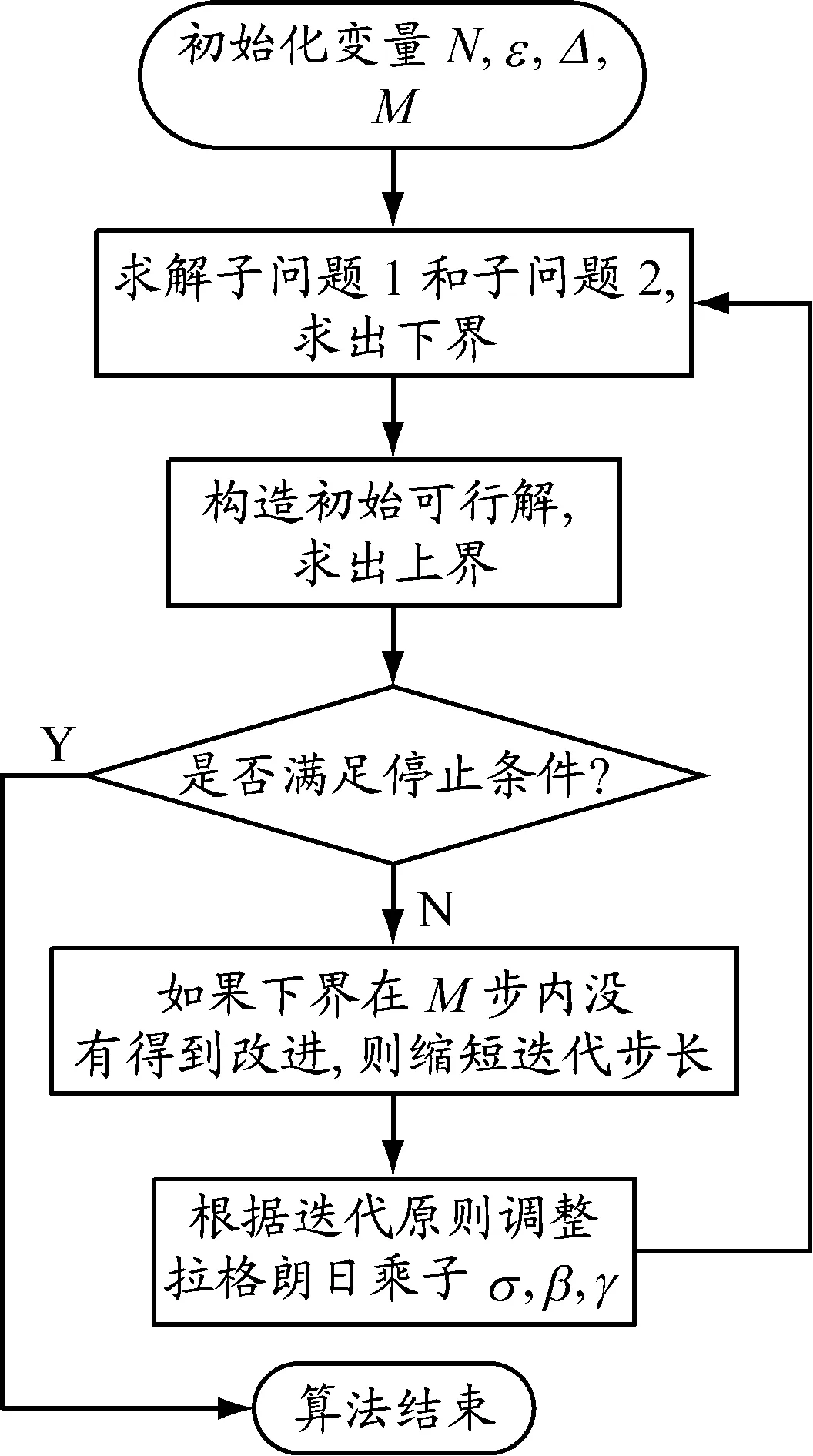
圖2 拉格朗日松弛算法流程

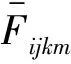
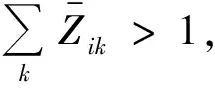
步驟5判斷解是否滿足停止原則：迭代次數小于N且(Zb-ZL)/ZL>ε(ZL是迭代過程中找到的最佳拉格朗日乘子，Zb代表目標函數的最佳可行解).若是，轉步驟7；若否，轉步驟6.

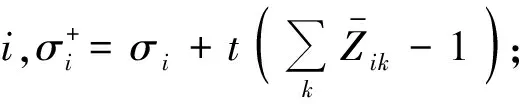
步驟7停止計算，輸出最優解.

4 算 例

4.1 基本數據

考慮一個由10個港口組成的班輪海運網絡，為簡化計算，假設港口間的正向貨流量與逆向貨流量及其運價相等.港口間相互貨物運輸量及單位運輸成本見表1和2，表中:1為釜山港,2為大連港,3為上海港,4為廈門港,5為香港港,6為新加坡港,7為安特衛普港,8為鹿特丹港,9為漢堡港,10為南安普頓港.單位運輸成本為2012年8月亞歐航線市場均價.

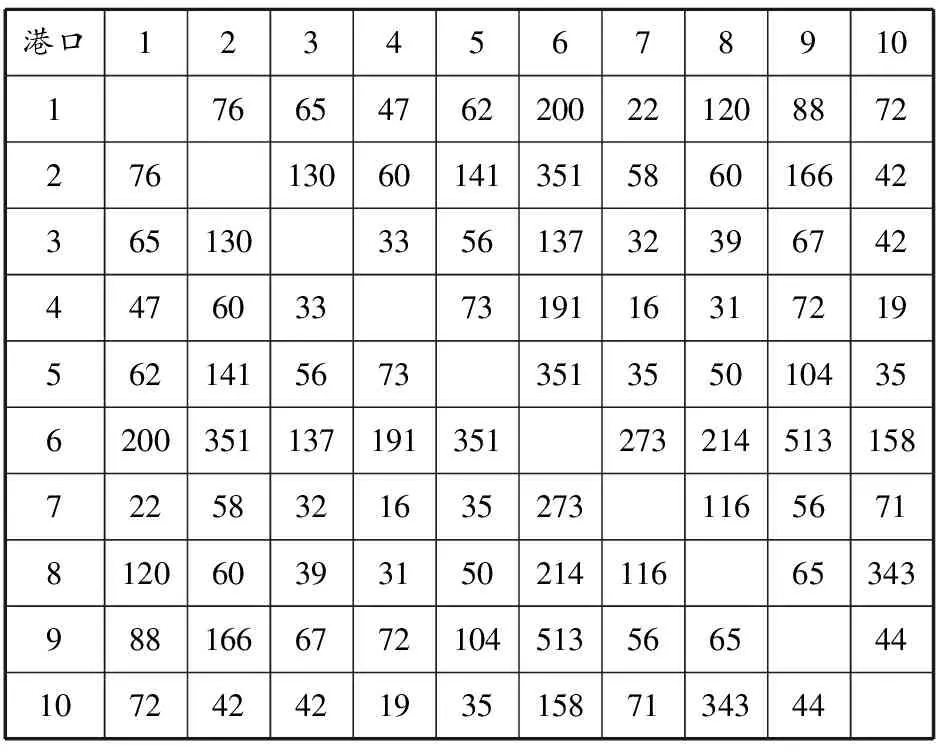
表1 港口間貨流量 103 TEU

計算前先將逆向貨流量與正向貨流量相加，計算時利用網絡的對稱性求解單向貨流量即可.在根據貨流量求出每一條可能運輸線路的運輸成本并計入樞紐港的擁堵成本之后，依據模型最終可以得到樞紐港的選擇結果.

4.2 算例結果及分析

算法設計用MATLAB實現，具體參數設置：N為1 000次，ε為0.01,M為10,Δ為2.

表3～5列出當a，b，p和α取不同數值時的計算結果:第1列表示樞紐港個數;第2列與第3列分別給出擁堵成本函數參數a和b，對a選取(1，5，10)，對b選取(1.1，1.5，1.7，2.0)，通過不同的a與b的組合考察參數的選擇對結果的影響;第4～6列列出各樞紐港(H1,H2,H3)的貨流量占總貨流量的比重;為檢驗模型對網絡中擁堵的控制效果，表中第7列引入貨流量不平衡比(即在所有的樞紐港中，貨流量最大者與最小者之比)以體現設計模型的初衷是分散貨流、降低擁堵;第8列給出樞紐港選擇的計算結果;最后一列給出所有情況下的總成本.

計算表明，當樞紐港的個數取2和3時，所得到的結果分別是(5，6)，(5，8)，(5，6，8)，模型選擇的樞紐港口基本符合現有集裝箱海運網絡的真實格局.通過對各表的數據進行分析可以得出以下幾點：

(1)規模經濟系數α對結果的影響.隨著α的逐漸增大，規模經濟效應越來越不顯著，從結果中可以看到總成本隨著α的增大有一定的增長.同時，a的變化對結果的影響也體現在貨流量不平衡比上，α越小則初始的不平衡比越大，說明為追求規模經濟效應，貨流量集中于某些關鍵節點之上.反之α越大，初始的不平衡比越小，規模經濟效應越不明顯.

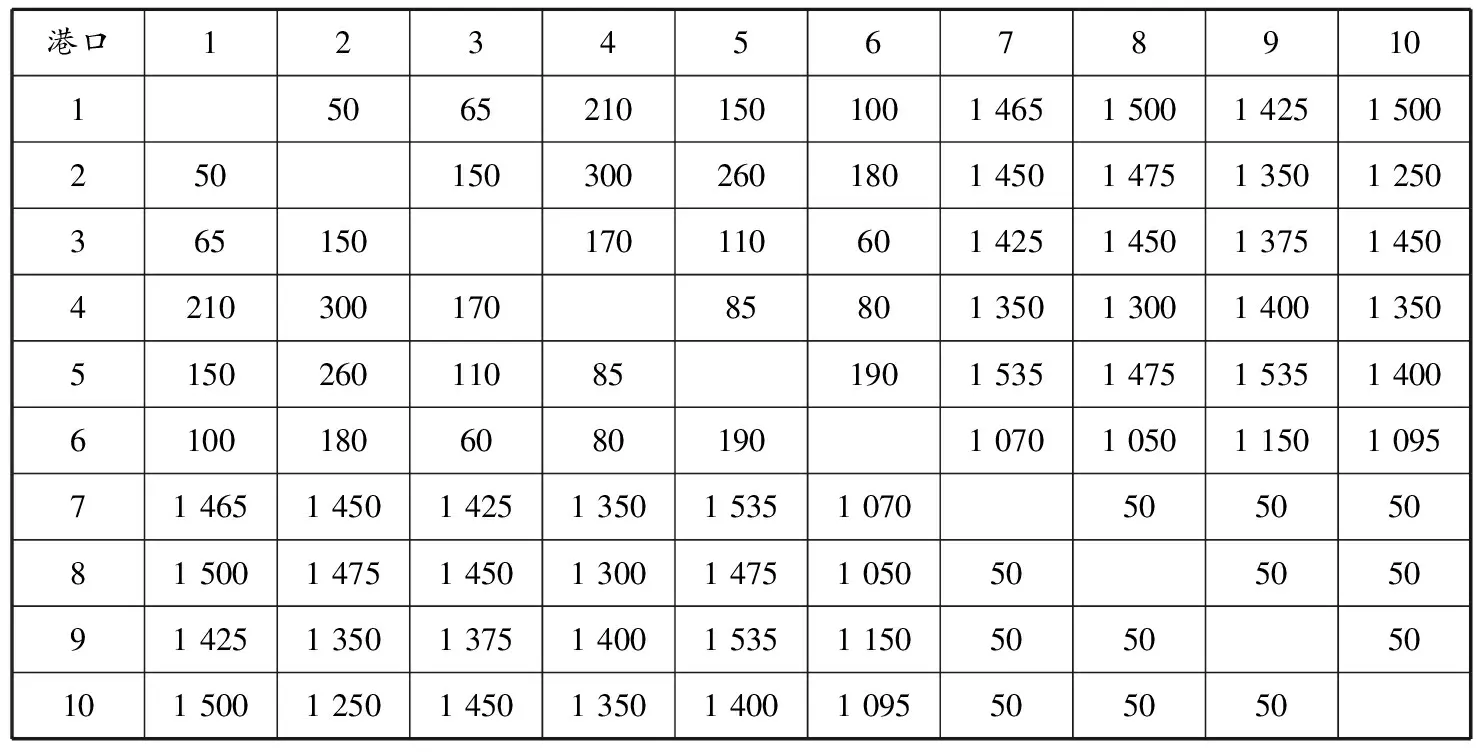
表2 港口間貨物單位運價 美元/TEU

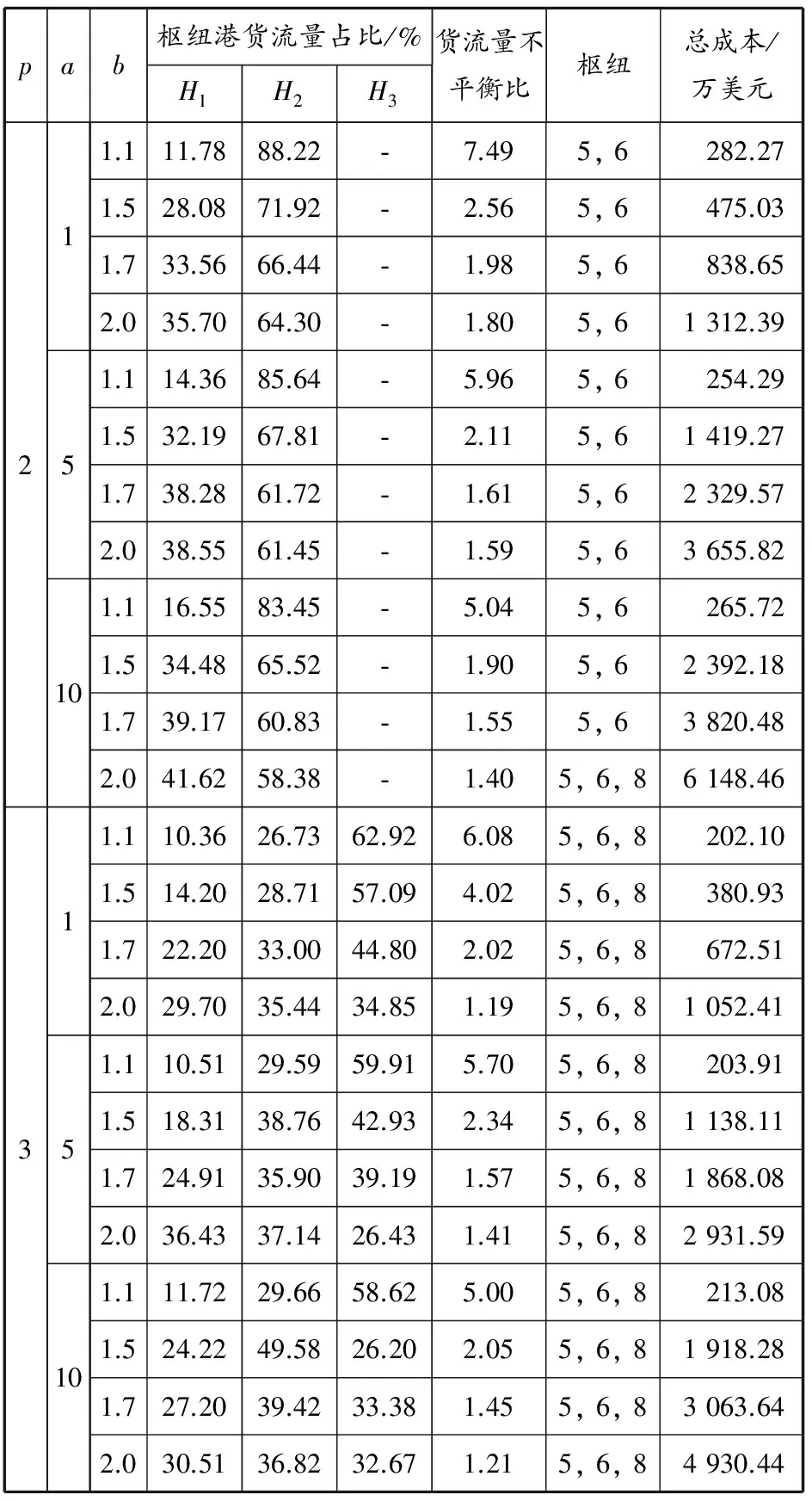
表3 10節點網絡計算結果 (α=0.2)

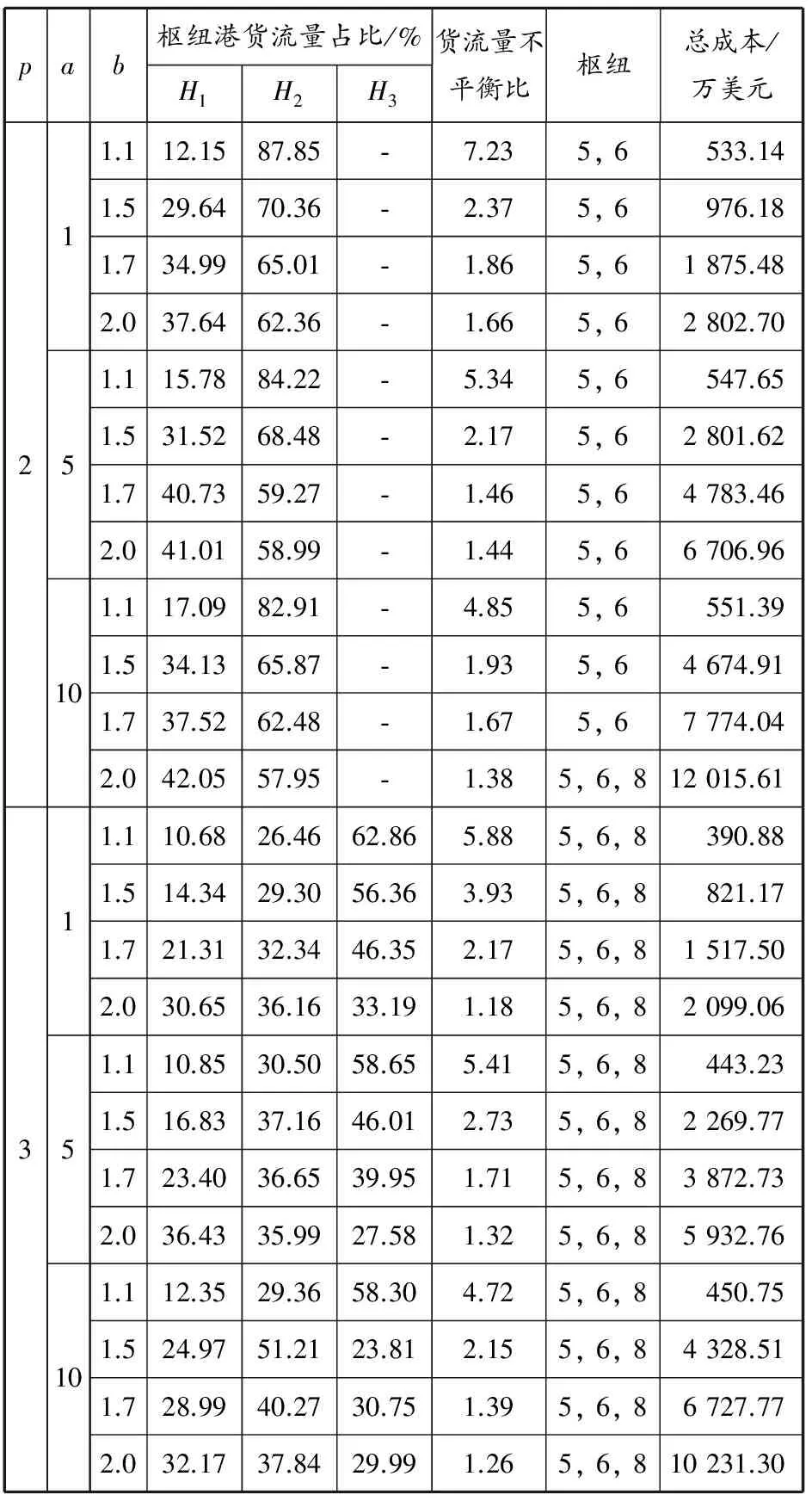
表4 10節點網絡計算結果 (α=0.4)

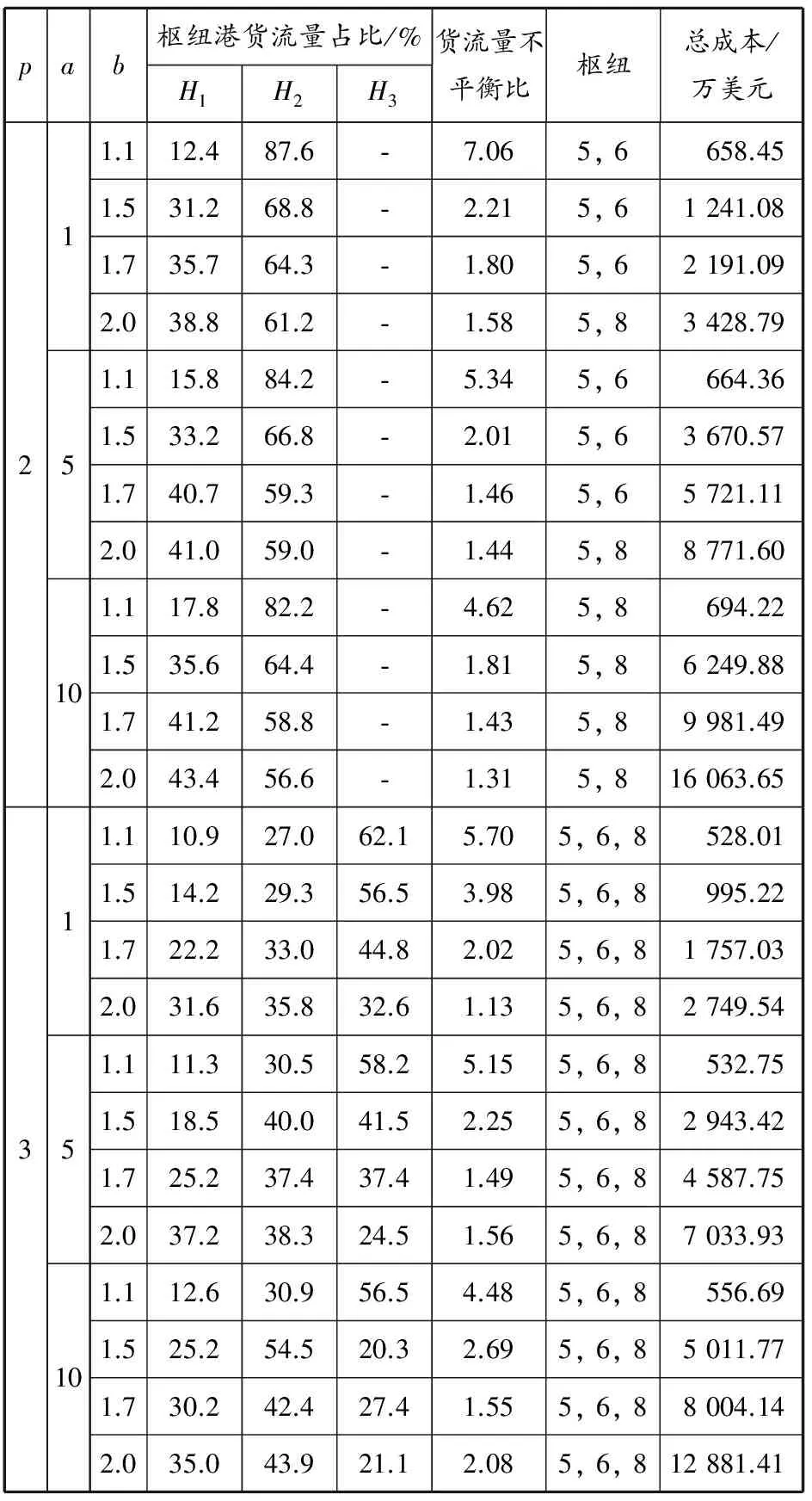
表5 10節點網絡計算結果 (α=0.6)

(2)樞紐港個數對結果的影響.在保持參數a和b不變的前提下，包含更多樞紐港的網絡總是有著更低的總成本.這是因為:一方面更多的樞紐港意味著在彼此之間的通路上可以利用更多的規模經濟效應，從而降低運輸成本；另一方面更多的樞紐港可以為運輸路線的制訂提供更大的選擇余地，使之可以選擇成本更低的路線.

(3)擁堵成本函數參數對結果的影響.引入的擁堵成本函數能夠將擁堵效應轉化成為經濟成本，量化地反映擁堵對整個運輸體系帶來的不利影響.當a和b逐漸增大時，總成本隨著擁堵成本的上升而增大，不同a與b的組合對結果產生一定的影響.不過某些港口在案例計算中始終出現在結果中(如新加坡港)，這說明擁堵成本函數的參數雖然可以改變某些情況下的計算結果，但港口本身的屬性可能是更加具有決定性的因素.隨著a和b的逐漸增大，貨流量不平衡比在所有的計算結果中均出現逐漸下降的趨勢，說明擁堵成本函數對網絡中貨流量的分配的確起著關鍵作用，有助于改善網絡中由于過度追求規模經濟效應而造成的部分節點流量過大的現象.

5 結束語

港口擁堵對整個集裝箱海運系統造成嚴重的經濟損失，已成為全球航運業面臨的一項難題.本文針對樞紐港的擁堵現象，建立基于擁堵控制的樞紐港選擇模型.該模型可以在現有的海運網絡中進行樞紐港的優化選擇、合理進行資源調配，并且可以作為班輪公司制訂運營計劃時的參考依據.

從宏觀的角度看海運網絡，該模型認為過度追求規模經濟效應是造成港口擁堵的一個因素，而通過平衡各樞紐港間的貨流量可以達到緩解港口擁堵的目的.對于班輪公司而言，優化海運網絡可以更有效地幫助改進航線設計、節約成本以獲得更多利益.

從擁堵控制的角度審視當前軸輻式海運網絡的組織,為海運網絡設計問題和相關研究提供一個全新的角度，只有更全面地考慮港口擁堵發生的原因才能更有效地完善海運網絡.當然，該模型仍然有很多值得改進之處，未來的研究重點將著力拓展模型的各項設定使其更加符合海運網絡的實際情況.

參考文獻：

[1] O’KELLY M E. A quadratic integer program for the location of interacting hub facilities[J]. Eur J Operational Res, 1987, 32(3): 393-404.

[2] AYKIN T. Lagrangian relaxation based approaches to capacitated hub-and-spoke network design problem[J]. Eur J Operational Res, 1994, 79(3): 501-523.

[3] ERNST A T, KRISHNAMOORTHY M. Solution algorithms for the capacitated single allocation hub location problem[J]. Annals Operations Res, 1999, 86(0): 141-159.

[4] YAMAN H, CARELLO G. Solving the hub location problem with modular link capacities[J]. Computers & Operations Res, 2005, 32(12): 3227-3245.

[5] EBERY J, KRISHNAMOORTHY M, ERNST A,etal. The capacitated multiple allocation hub location problems: formulations and algorithms[J]. Eur J Operational Res, 2000, 120(3): 614-631.

[6] da GRA?A COSTA M, CAPTIVO M E, CLíMACO J. Capacitated single allocation hub location problem: a bi-criteria approach[J]. Computers & Operations Res, 2008, 35(11): 3671-3695.

[7] 李莉, 丁以中. 軸輻式快遞網絡的樞紐選址和分配優化[J]. 上海海事大學學報, 2012, 33(2): 33-39.

[8] 陳淑文. 港口擁堵難題危及全球海運系統[J]. 中國遠洋航務, 2007(3): 24-25.

[9] 壽建敏. 港口擁堵催生多式聯運和世界海運格局的變化[J]. 集裝箱化, 2005( 9): 41-43.

[10] FAN L, WILSON W W, DAHL B. Congestion, port expansion and spatial competition for US container imports[J]. Transportation Res Part E: Logistics & Transportation Rev, 2012, 48(6): 1121-1136.

[11] LEACHMAN R C, PAYMAN J. Congestion analysis of waterborne, containerized imports from Asia to the United States[J]. Transportation Res Part E: Logistics & Transportation Rev, 2011, 47(6): 992-1004.

[12] CHEN G, GOVINDAN K, YANG Z Z. Managing truck arrivals with time windows to alleviate gate congestion at container terminals[J]. Int J Production Econ, 2013, 141(1): 179-188.

[13] MENG Q, WANG X C. Intermodal hub-and-spoke network design: incorporating multiple stakeholders and multi-type containers[J]. Transportation Res Part B, 2011, 45(4): 724-742.

[14] 靳志宏, 蘭輝, 孫威, 等. 集裝箱多式聯運協調計劃的分級優化[J]. 上海海事大學學報, 2010, 31(1): 21-27.

[15] 白治江. 動態負載下堆場資源規劃的在線決策[J]. 上海海事大學學報, 2010, 31(3): 52-57.

[16] de PALMA A, MARCHAL F. From W Vickrey to large-scale dynamic traffic models[C]// 26th Eur Transport Conf, Loughborough University. Australia: ARRB Group Limited, 1998.

[17] GILLEN D, LEVINSON D. The full cost of air travel in the California corridor[J/OL].Transportation Res Rec 1662, 1999: 99-0305[2012-01-12]. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1089084.

[18] Federal Aviation Administration. Airport capacity and delay (AC 150/5060-5) [R/OL]. (1983-09-23)[2012-02-26]. http://www.faa.gov/regulations_policies/advisory_circulars/index.cfm/go/document.information/documentID/22824.