利用畫圖表征,促進“倍”的理解
林俊峰 謝玉娓
一、新、舊教材比較與分析
(一)體現了“情境+問題串”的編寫體例特點,為教與學導航
新教材基于“情境”,圍繞一定目標(引導學生逐步理解倍的意義),按照一定的結構精心設計了一組問題,通過這三個問題指向數學知識、方法、思想等發(fā)生發(fā)展過程,從而引領學生的學習過程,有效實現學習目標。這正體現了新版教材“情境+問題串”的編寫體例特點,這樣的編寫有利實現啟學引思、導學引教。
(二)新增了“學生作品”,更重視合理利用畫圖表征,促進學生對“倍”意義的理解
1.新增了學生作品,凸顯學生主體地位。一是強調通過圖形直觀,經歷把“3只猴子圈在一起看成1份,6只小鴨子就有這樣的2份,鴨子數就是猴子數的2倍(6是3的2倍)”的認識過程,即在活動中親身經歷了“倍”的形成過程,同時在這一過程中滲透了畫圖策略。二是在學生畫圖的過程中,讓教師及時讀懂學生的想法與認知困難,及時采取跟進的教學策略。
2.增加了畫圖表征的分量,強調其重要性。
新版教材增加了畫圖表征的分量,這樣在實物操作與抽象思維之間架起了橋梁,讓學生在圈一圈、畫一畫中初步建立“倍”的表象,并且有利于學生有效表達自己構建的概念表象,與教師、同伴交流,促進概念的初步形成。
(三)溝通“倍”與除法意義的聯系,強調舊知對新知學習的正遷移
新教材增加了一幅“對話圖”,即笑笑與智慧老人的對話。不僅有利于教師對教學的把握和學生對學習內容的理解,也凸顯了編者強調要溝通“倍”與除法意義的聯系,重視學習的正遷移,將新知納入學生的已有認知結構中。
二、教學建議
只有掌握了概念的本質屬性,才能提高學生分析問題和解決問題的能力。“倍”的本質屬性是什么?“倍”是兩個量比較的結果,以一個量為標準,另一個量有這樣相同的幾份就是它的幾倍。怎樣才算理解了“倍”?例如,當學生看到“6是3的幾倍”或“2的3倍是多少”這樣具有乘法結構的描述時就能在腦海中呈現一幅結構表象圖;或者當學生能用畫一畫、說一說等舉例說明“什么是2倍”時,我們就認為學生理解了“倍”。
基于第一部分的教材分析,筆者認為教學中要充分利用學生對“乘、除法意義”的認識以及有關“一份”和“幾份”的經驗,將它們作為學習新知的生長點和支撐點,通過認知的同化(都是求“一個數里含有幾個另一個數”),把“倍”的認識納入學生已有的認知結構中。在教學中,通過大量的操作活動,借助畫圖表征的功能,不斷豐富學生的表象,凸顯概念的結構關系。并且不斷進行對比與抽象,完成將“倍”從“形”到“數”的轉化,逐步豐富“倍”知識的表象,深化對“倍”知識的理解。
(一)找準教學生長點,溝通新知與舊知的聯系
學生在之前的學習中已經認識了乘法和除法的意義,也具有“份”的生活經驗。因此將“倍”的認識建立在“份”和除法的意義之上,有利于幫助學生溝通新知與舊知之間的聯系,較順利地把“倍”的認識納入學生已有的認知結構中。
教學中,教師呈現主題圖引導學生數出各種小動物的數量,讓他們比一比小猴子和小鴨子的數量。通常,學生能運用以前的學習經驗,提出“比多比少”與“求和”這樣的“加法結構”的問題,很少有學生能用“倍”來比較兩種小動物的只數(即使極少數學生說出“倍”,也并不知道其含義)。此時,教師可告知學生,除了對小猴子和小鴨子進行比多比少外,還可以從另一個角度來比較。首先,教師要充分結合直觀圖,進行圈一圈、畫一畫,指出:把小猴的只數看作1份,小鴨子的只數就有這樣的2份,我們就說小鴨子的只數是小猴子的2倍,也就是6是3的2倍。其次,教師還應引導學生將“倍”和除法意義聯系起來,把小鴨子的只數每3只看成1份,6里面有這樣的2份,也就是說6里面有2個3,用除法算式6÷3=2來表示(提醒學生這里2的后面不寫單位名稱,因為倍是表示兩個數量間的一種關系,不是單位名稱)。
(二)利用“形”的直觀,初步建立“倍”的表象
在學習“倍”時,常有學生認為“6比3多2倍”,可見,學生對“倍”的認識受到“比多比少”學習的負遷移,也說明學生未掌握“倍”的概念的本質屬性。認知心理學認為,概念形成其實可以概括為兩個階段,即從完整表象上升為抽象概念,實現抽象概念在思維過程中的具體再現。在這兩次必備轉換過程中形成完整表象是最重要的一個環(huán)節(jié)。而由于低年級學生表達能力的欠缺,讓學生通過畫圖表征來表達出自己構建的概念表象就顯得尤為重要。
在比較完小猴子與小鴨子的只數后,教師要引導學生模仿著畫一畫、圈一圈、說一說:把誰看成1份,誰是誰的幾倍?而后,讓學生也用畫圖表征的方法,來比較圖中其他動物只數間的關系,要求畫出的圖要能清楚地看出誰是誰的幾倍。在交流中要讓學生體會到:不同只數的動物間的倍數關系可能是相同的(小鴨子的只數是小猴子的2倍;松鼠的只數是孔雀的2倍),也可能是不相同的(小鴨子的只數是小猴子的2倍;小雞的只數是松鼠的4倍);而同樣的小鳥只數與不同動物只數比較,它們的倍數關系是不同的。最后,引導學生用除法算式表示出這些倍數關系。在這一過程中,要逐步引導學生體會:在比較兩種動物的只數時,把一種動物的只數看作1份,再看另一種動物的只數里有幾個這樣的1份,就是它的幾倍。
這樣,學生接觸大量實物間的倍數關系素材,通過畫圖表征(圈一圈)凸顯了“倍”的概念本質,幫助學生初步理解了“倍”的概念。
(三)在不斷對比與抽象中,逐步理解倍的意義
如何讓學生進一步理解“倍”的概念呢?這就需要在不斷對比與抽象中,舍棄各種不相干的因素,在變化中抓住“不變”,而這“不變”就是它們的量性特征,就是“倍”的本質。
1. 一倍數不變,幾倍數變化。
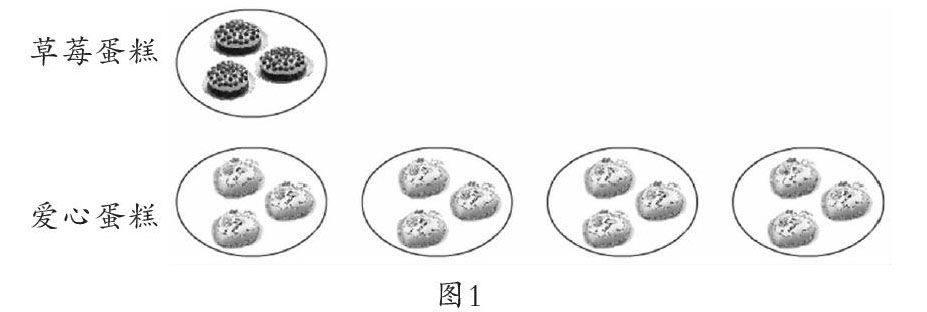
(1)出示蛋糕圖(如圖1所示),美羊羊做了3個草莓蛋糕和12個愛心蛋糕。請問:愛心蛋糕的個數是草莓蛋糕的幾倍?
在學生回答并說出是怎么想的后,課件又逐份增加愛心蛋糕,追問:現在愛心蛋糕的個數是草莓蛋糕的幾倍?你是怎么想的?
(2)客人們吃了一些愛心蛋糕,現在,愛心蛋糕的個數是草莓蛋糕的幾倍?課件逐份減少愛心蛋糕,最后屏幕上剩下草莓蛋糕、愛心蛋糕各3個,討論中明確:把草莓蛋糕看作1份,愛心蛋糕也有這樣的1份,我們就說愛心蛋糕是草莓蛋糕的1倍,也可以說草莓蛋糕是愛心蛋糕的1倍,此時,兩種蛋糕的個數是一樣的。
討論:草莓蛋糕一直都是3個,為什么愛心蛋糕的個數是草莓蛋糕的幾倍卻一直在變化呢?
師:如果愛心蛋糕有這樣的7份呢?10份、100份呢?你發(fā)現了什么?
小結:把草莓蛋糕看成1份,愛心蛋糕有這樣的幾份就是草莓蛋糕的幾倍。
2. 幾倍數不變,一倍數變化。
懶羊羊也學著制作蛋糕,它做了12個愛心蛋糕,還做了一些草莓蛋糕,請問:愛心蛋糕是草莓蛋糕的幾倍?(討論后歸納:倍是兩個量在比較,不知道草莓蛋糕的個數,就無法比較)
師:看來1份草莓蛋糕有幾個太關鍵了,大家猜猜,草莓蛋糕可能有幾個?這時,愛心蛋糕是草莓蛋糕的幾倍?
討論:愛心蛋糕一直是12個,為什么兩種蛋糕之間的倍數關系卻發(fā)生了變化?
討論后明確:愛心蛋糕和草莓蛋糕在比較,這里要看草莓蛋糕有幾個,它是我們比的標準,標準變了,倍數也就發(fā)生了變化。
3. 倍數不變,一倍數變化。
師:請你在本子上畫一畫,第一行畫圓形,想畫幾個就畫幾個,在第二行畫三角形,讓三角形的個數是圓形的2倍。(學生獨立畫,教師巡視。完成后全班交流、反饋)
討論1:要求畫出的三角形的個數必須是圓形的2倍,可是為什么大家畫出的三角形的個數卻各不相同呢?
生:因為第一行畫出的圓形的個數都不相同,它的2倍也就不相同了。
師:那么請你們再想一想,盡管圓形和三角形的個數不盡相同,但有一樣是相同的,那就是……
生:三角形的個數都是圓形的2倍。
討論2:為什么三角形、圓形的個數各不相同,可是三角形的個數卻都是圓形的2倍呢?
生:因為把圓形的個數看成1份,三角形的個數里始終有這樣的2份,所以就是圓形的2倍。
師:是啊,只要三角形的個數里有2份圓形的個數那么多,我們就說三角形的個數是圓形的2倍。
這樣,通過以上一系列“變與不變”的對比活動,學生在圈一圈、畫一畫、說一說中進一步明確:以一方為標準,另一方有這樣相同的幾份就是它的幾倍,建構了倍的直觀模型。
(作者單位:福建省泉州師范學院附屬小學 本專輯責任編輯:王彬)

