正確理解教學目標 創造性地使用教材

梁紅云

蘇教版教材在五年級上冊“小數乘法與除法練習”中，安排了這樣三道綜合練習題。

10.先計算，再把每題的積和第一個因數比一比，有什么發現？

4.9×1.01 5.8×1.2 3.15×1.4

4.9×1 5.8×1 3.15×1

4.9×0.99 5.8×0.8 3.15×0.6

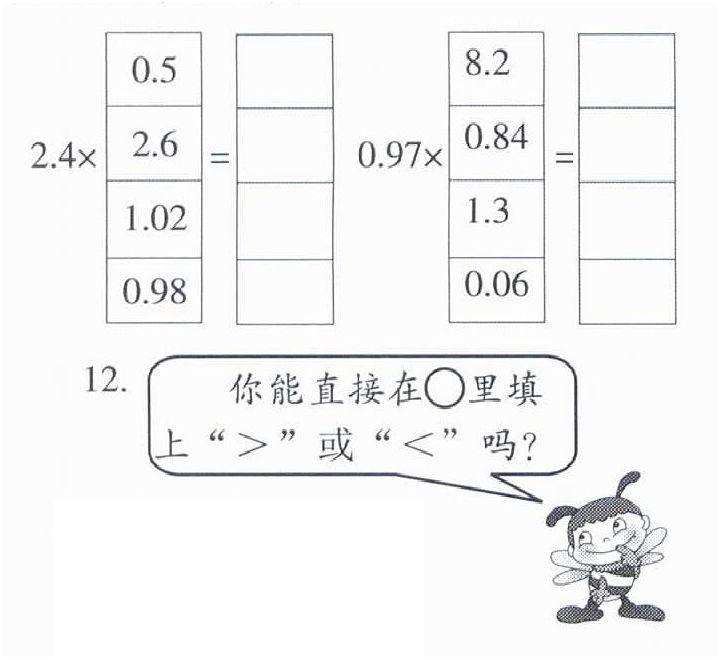
11.先說出每次乘的積比第一個因數大還是小，再計算。

12.

1.4×2.8○2.8

0.63×0.9○0.63

0.85×1.3○0.85

0.8×1.3○1.3

教材編排的意圖很明顯：第10題讓學生通過計算和比較，體會小數乘法中存在的一些有趣的規律，進而提高學生對乘積大致范圍的估算能力：一個數與1相乘，積與原數相等；一個數與比1大的數相乘，積大于原數；一個數與比1小的數相乘，積小于原數。通常我們會這樣組織教學：先讓學生獨立算出第10題每組三道題的得數，再引導學生一組一組地進行觀察，說說每題的積與第一個因數比較，是大一些，還是小一些；然后再引導學生進一步思考“為什么每組第一題的積都比第一個因數大，第二題的積都與第一個因數相等，第三題的積都比第一個因數小”，從而發現規律。但在教學過程中我發現，這樣的教學設計，讓學生一開始就陷入了機械、枯燥的計算和改錯中，極易造成他們的心理疲勞，而且耗時較多，學生不僅不容易發現題目中所蘊含的規律，還不易理解“兩數相乘，積怎么會比因數還小”。于是我尋思怎樣才能讓學生學得既輕松、積極，又能習得知識和方法。最后，我決定把生活中的實際問題引入課堂，便于學生利用自己已有的生活經驗進行估算，在理解的基礎上自主概括出其中的數學規律。

出示問題：小明每小時行3.4千米，他1.5小時行多少千米？0.8小時行多少千米？

學生解答問題后，我讓學生說說用豎式計算小數乘法時應該注意些什么。（課件出示橫式和豎式，意在復習鞏固已學知識）

師：為什么3.4×1.5的結果大于3.4，而3.4×0.8的結果小于3.4？（板書“3.4×1.5>3.4，3.4×0.8<3.4”，引導學生結合實例及乘法分配律加以解釋）

生1：因為1.5小時比1小時多，1.5小時行的路程也比1小時行的路程多，所以3.4×1.5的結果大于3.4；0.8小時比1小時少，0.8小時行的路程也比1小時行的路程少，所以3.4×0.8的結果小于3.4。

師：你能結合實例來說明理由，真聰明！

生2：因為1.5小時比1小時多半小時，所以1.5小時行的路程也比3.4千米多3.4千米的一半，也就是比3.4千米多1.7千米；而0.8小時比1小時少0.2小時，所以0.8小時行的路程也比3.4千米少3.4×0.2千米，也就是比3.4千米少0.68千米。

師：你說得更具體了，并且老師從你的發言中聽出了乘法的分配律。

生3：對，還可以用乘法分配律加以解釋。3.4×1.5=3.4×（1+0.5）=3.4×1+3.4×0.5=3.4+1.7，所以3.4×1.5的結果大于3.4；3.4×0.8=3.4×（1-0.2）=3.4×1-3.4×0.2=3.4-0.68，所以3.4×0.8的結果小于3.4。

師：（板書學生的計算思路）你能用乘法分配律來說明理由，說明你的思維更深刻了！結合剛才的認識，請大家想一想3.4×1.01，3.4×1，3.4×0.99這三道算式的積分別與3.4相比，誰大誰小？

（學生大膽猜想。老師板書：3.4×1.01○3.4 3.4×1○3.4 3.4×0.99○3.4）

師：到底大家的判斷對不對呢？請同學們算一算，驗證一下，好嗎？

（學生計算驗證，匯報）

生：3.4×1.01>3.4，3.4×1=3.4，3.4×0.99<3.4。

師：看著這些算式，大家還能想到什么數學問題？

生1：3.4乘比1大的數，積一定比3.4大；3.4乘比1小的數，積一定比3.4小。

生2：一個數與比1大的數相乘，積大于原數；一個數與比1小的數相乘，積小于原數；一個數與1相乘，積與原數相等。（老師根據學生的回答，把學生的思路在黑板上記下來：一個數×比1大的數>原數；一個數×1=原數；一個數×比1小的數<原數）

學生的答案，是結合現有的經驗體會進行的初步歸納，教師此時不必過于計較表達的嚴密性，更不宜立即圍繞數0進行抽象的分析、判斷。此時，學生的思維正處于活躍狀態，我順勢追問了一句：“你們都同意這位同學的說法嗎？”學生異口同聲地回答：“同意！”我微微一笑，既不肯定，也不否定，在等待著是否有不同的聲音。果然，有幾名學生低聲說出了我期待的聲音：“一個數不能是0。”不少學生在連連點頭。我點到即止，接著出示了下列兩組題，先讓學生比較大小、說理，再任選一組計算驗證。

2.4×1.02○2.4 8.2×0.97○0.97

2.4×0.98○2.4 0.06×0.97○0.97

這樣，我精簡了教材第11題的計算量，選擇了有代表性的兩組題，讓學生不僅懂得了將積與第一個因數進行比較，還會與第二個因數進行比較，進一步驗證和應用規律。

最后我出示了這個問題：小明做了四道計算題，你不用計算，能幫他判斷哪道題的結果是錯的嗎？說說理由。

1.4×2.8=2.72 0.85×1.3=0.1105

0.63×0.9=0.968 0.8×1.3=1.34

我引導學生使用多種判定方法：根據本節課學習的規律來判斷，根據積的末位（或首位）上的數字來判斷，根據積的小數位數來判斷。這一題，是對教材第12題的改編，不僅可以加深學生對規律的理解，還可以讓學生用上之前學過的與小數乘法相關的知識來解決問題，學生的思維更加活躍了。

這節課的課堂氣氛很熱烈，師生互動、生生互動，學生的思維異常活躍。這都源于教師創造性地使用教材，關注學生的認知起點，充分利用學生已有的生活經驗和學習經驗，為學生提供了探索規律的機會與空間，讓學生經歷了感悟規律、體驗規律和運用規律的過程。

本節課研究積與因數的大小關系，但教學的最終目標并不是讓學生機械地掌握“一個數與1相乘，積與原數相等；一個數與比1大的數相乘，積大于原數；一個數與比1小的數相乘，積小于原數”這個規律，而是讓學生理解這個規律，并能自覺地運用這個規律對乘積的大致范圍進行估算，促進學生直覺思維能力和數感的發展。

（責編 白聰敏）