大班數學學習困難兒童的個案干預研究

李正清　周欣　康丹　田麗麗　呂雪　程陽春　徐晶晶

【摘要】研究者以數學操作游戲為方法對一位大班數學學習困難兒童進行了干預，同時輔以自我覺錯能力的訓練。結果表明，干預和訓練后該兒童的數數、運算、書面符號表征及理解等能力均有不同程度的提高。由研究結果可知，以數學操作游戲為方法進行個別化干預同時輔以自我覺錯訓練，是一條提高數學學習困難兒童數學能力的有效途徑。

【關鍵詞】早期數學學習困難；游戲操作；自我覺錯；個別干預

【中圖分類號】G612 【文獻標識碼】A 【文章編號】1004-4604（2013）07/08-0010-07

早期數學學習困難（Mathematics LearningDisability）兒童是指智力發展正常，但數學發展水平顯著低于同齡人的兒童。有研究表明，有8%左右的兒童存在數學學習困難。根據教育部2010年的相關統計數據，我國5歲以上在園幼兒有848.7萬人。按照8%數學學習困難的檢出率，我國約有67.9萬名5歲以上在園幼兒可能存在數學學習困難。有研究指出，學前班兒童的數字感能力能有效預測兒童小學三年級甚至整個小學階段的數學學業成績。因此，盡早發現年幼兒童的數學學習困難并進行及時干預，能夠為他們后續數學能力的發展提供幫助。

對學習困難成因的解釋有多種理論，如成熟滯后理論、行為缺陷理論、認知缺陷理論和元認知理論等，各種理論都試圖提出了相應的干預方法。有研究證明。以元認知理論為基礎的學習策略訓練可能是一種較有效的干預措施。例如，努力提高兒童元認知能力中的自我覺錯能力就有助于改善數學學習困難兒童的狀況。自我覺錯能力是指練習者將練習后獲得的反饋與已習得的正確參照進行多次比較后形成的獨立覺察自己錯誤的能力。

本研究以數學游戲為方法，對個案數學學習困難兒童進行干預，同時輔以自我覺錯能力訓練，以期改善其數學學習困難狀況，并探討對類似兒童進行干預的有效途徑。

一、研究設計

（一）被試的選取與診斷

被試為上海市某幼兒園大班幼兒Y。Y，男，6歲，順產，身體健康，無重大疾病史。父親為公司主管，初中文化水平；母親為家庭主婦，小學文化水平；家庭經濟條件一般。老師對其數學能力的評價常常是負面的。Y語言能力一般，喜歡參與建構游戲，社會性發展良好，較受同伴歡迎。在幼兒園集體活動中，Y經常表現出注意力分散，數學能力較弱。

1.對Y數學學習能力的鑒定

使用Ginsberg和Broody開發的兒童早期數學能力測驗（Test of Early Mathematics Ability，簡稱TEMA）對Y的數學學習能力進行了測查。Y的TEMA原始分為28分，數學能力分為99分。Y的數學能力分比另一個5歲兒童樣本（N=299）TEMA能力分的平均值M=122分（SD=10.46）低了近2個標準差。因此，研究者將Y確定為數學學習困難兒童。但在我們后續確定的一個數學學習困難兒童樣本（N=35；TEMA能力分平均值M=98.49，SD=8.66）中，Y的TEMA得分達到了平均分數水平，因此，我們判斷Y的數學學習困難程度是相對較輕的。

2.對Y數學學習困難的問題診斷

（1）測查診斷

采用周欣編制的《數學學習困難兒童數和數量關系理解診斷性測查》對Y進行測查。結果表明，Y在實物水平的計數、集合比較、加減運算、序數和個位數認讀等方面表現較好，但在書面數符號表征能力方面有明顯缺陷。

（2）觀察診斷

盡管測查診斷表明Y具備基本的數學能力，但研究者在實際觀察中發現Y有如下表現：唱數水平表現不穩定，有時能唱數至50以上，有時只能唱數至20左右：寫數字時經常報告“我忘記這個數怎么寫了”：基本沒有數的組成與分解的相關經驗；可借助實物（如手指）運用“全部數”策略進行10以內的加減運算，結果有時正確有時錯誤，有時能運用策略有時則屬胡亂猜測。總的來說，Y在數數、數的組成與分解、書面數符號表征、口頭加減運算等方面的表現很不穩定。

（二）干預思路與計劃

1.干預內容

已有研究表明，數概念是兒童數學能力發展中的“中心概念”，它的發展不僅與兒童今后的數學學習有著直接聯系（Griffin，Case&Siegler，1994），而且與兒童的思維能力發展也有著密切關系。因此，本研究重點對個案兒童的基本數學認知和技能進行干預，包括數數技能、數的組成與分解能力、書面符號的表征和理解能力、口頭加減運算。

（1）數數技能

數數包括三個子技能：按照正確的順序有聲或無聲地說出數詞；能確認可用于計數的若干單位實體；能把數詞和計數的單位實體一一對應起來。其中，一一對應包括數詞和指示動作之間在時間上的一一對應以及指示動作和物體之間在空間上的一一對應（Fuson，1988）。

（2）數的組成與分解

對數的組成與分解的理解與掌握，是幼兒進一步學習加減運算的基礎。在組成、分解的過程中存在著三個相互聯系的數群和子群，一個數群（總數）可以分解成兩個相等或不相等的子群（部分數），兩個相等或不相等的子群以互補和互換的相互關系統一在一個數群之中。

（3）書面數符號表征和理解

數符號系統是一個包含了幾方面特殊數知識的網絡系統，如數詞、計數、書面數符號以及對數的表征等知識和技能。不少兒童在初學書面數符號時會有較大困難。如有些兒童在對具體數學問題和符號性數學表達式進行轉換時會產生困難；有些兒童盡管能閱讀和書寫數符號，但往往不理解數的位置與數值的關系。測查診斷發現，Y對10以內的數符號表征能力較弱，因此，研究者干預時著重加強Y對實物與表征之間關系轉換的理解，幫助Y理解數字與數量的關系。

（4）口頭加減運算

當對數的組成與分解的理解達到概念水平時，兒童便可以進行口頭加減運算了。研究表明，兒童一般到5歲半左右就會運用數的組成與分解來進行加減運算，接受過數的組成與分解方面學習的兒童在6歲半以后口頭運算能力會比以前有很大提高。因此，幼兒園大班兒童是完全有可能運用數的組合、分解方法來進行運算的。

2.干預策略

（1）運用注重操作的個性化學習方式

Clements（2000）認為，對數學學習困難兒童的矯治應盡可能使用多感覺通道訓練方式，即運用示范、角色扮演、展示、模擬和合作學習等方式，以激發和保持學習者的興趣。教師可以運用記憶術和游戲以幫助學習者記憶數字的組合。盡可能不作直接指導，多使用互動性的教學策略。為此，本研究主要采用數學操作游戲方式，結合個案兒童的興趣，進行靈活多樣的干預。

（2）呈現結果反饋，提高幼兒的覺錯能力

覺錯能力的形成需要練習者將內部反饋與外部反饋不斷進行比較對照。結果反饋（Knowledgeof Results，以下簡稱KIK）即是一種外部反饋。有關研究指出，在呈現KR.時需要注意兩點：一是由學習者來決定何時呈現結果；二是在練習期間不宜頻繁呈現KR。研究者在每次干預過程中都設置了讓Y進行自我檢查的環節，并在提出針對性提問時同時呈現KR.以引導其通過實際操作提高自我覺錯能力。具體過程舉例如下。

（飛行棋游戲中）

研究者：剛才你這樣走，對嗎？應該怎么走才對呢？

（Y仍然重復之前錯誤的走法。）

研究者：剛才你扔出的是幾？你走了幾步？相等嗎？你再試試看。

Y：5。（仍然重復之前錯誤的走法。）

研究者：不對（呈現KK）。耐心一些，慢慢再走一次。邊走邊想想，有什么地方不對？

（Y慢慢走棋，正確走出了相應的步數。）

研究者：很好。你前一次在數到3的時候走了兩步，剛才這次走對了。記住，嘴巴里每念一個數字手里只能走一步（呈現KK）。

3.干預計劃

Saxe等人提出，學前兒童的四種數水平是以先后順序發展的：數的指代性功能、對單個集合的表征、集合的比較或復制、簡單的加減運算。本研究的干預計劃也遵循這一發展規律，先從對Y數數技能、基數概念的干預入手，然后過渡到書面數符號的表征。再到形成數的組成與分解的相關經驗。最后發展到能進行加減運算及生活情境中的實際運用。

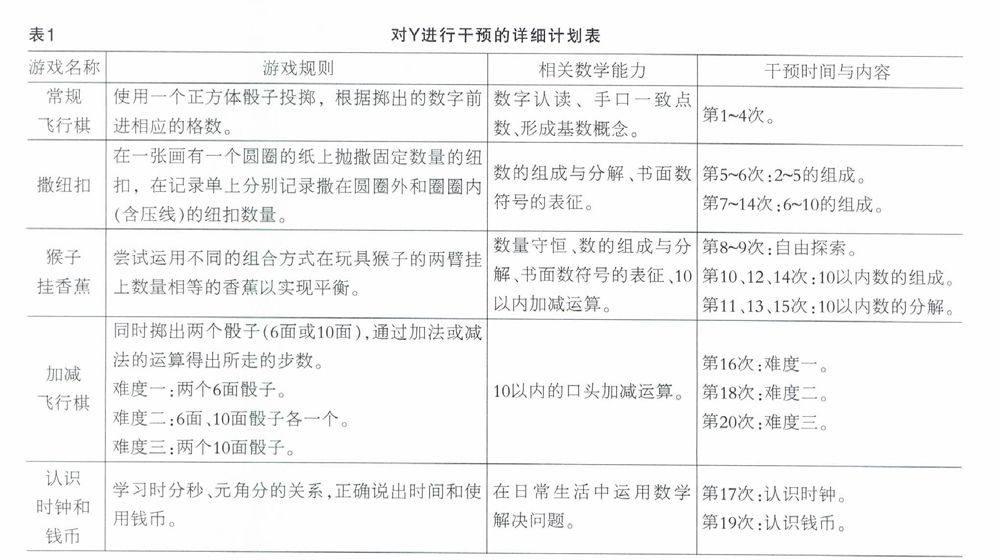
干預計劃從大班下學期開始，每周干預兩次，每次干預時長40分鐘左右。Y沒來幼兒園時，則將當次干預計劃向后順延。共計實施20次干預，總計800分鐘。具體干預計劃見表1。

二、干預過程

（一）關于數數技能

數數技能的干預主要通過“常規飛行棋”游戲來進行。在游戲初期，Y經常出現手口不一的情況，如走棋漏格、對同一格數了兩下等。當Y出現錯誤時，研究者要求Y自己判斷剛才的數數是否正確，若Y無法回答則呈現KR，并向Y指出錯誤的原因，要求Y重新走一次。隨著練習次數的增加，逐漸減少呈現K1K的次數，以讓Y主動進行自我覺錯。

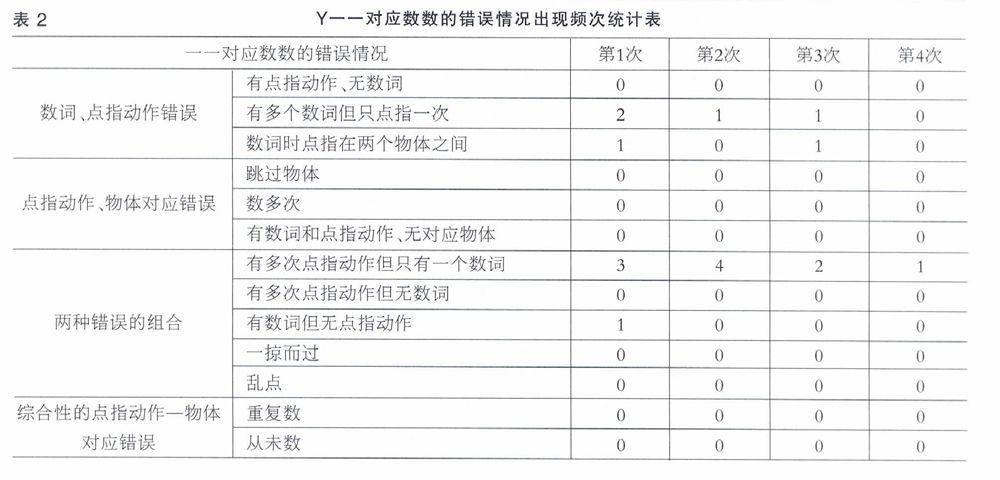
根據Fuson（1988）的《兒童數數的一一對應錯誤分類表》，研究者對每次干預中Y出現的錯誤情況及頻次進行了詳細記錄。由表2可知，經過4次干預，Y已經很少出現錯誤，能夠達到一一對應數數的目標。

（二）關于數的組成與分解

數的組成與分解的干預主要通過“撒紐扣”和“猴子掛香蕉”兩個游戲進行。掌握手口一致正確點數的技能是進行這兩個游戲的基礎，因此這部分干預安排在“常規飛行棋”游戲之后進行。“撒紐扣”游戲重點在于幫助Y積累數字組成與分解的感性經驗，“猴子掛香蕉”游戲的重點則在于讓Y通過實物操作進行驗證，鞏固已有的數經驗，為加減運算奠定基礎。

在干預前Y幾乎沒有關于數的組成與分解的經驗。因此研究者將“撒紐扣”游戲設計為從最簡單的數字“2”開始，然后逐步增加難度。其中，對“2～5的組成與分解”進行了兩次干預，對“6～7的組成與分解”進行了兩次干預，對“8～10的組成與分解”進行了六次干預。干預發現，Y對6以上數字的組成與分解表現較不穩定。

第8次干預時，先開始“撒紐扣”游戲，緊接著開展“猴子掛香蕉”游戲。開始時，研究者讓Y自己探索玩法。Y探索兩次之后，研究者結合“撒紐扣”游戲中數的組成與分解的內容，要求Y進行驗證性嘗試。例如，研究者在猴子的一只胳膊上先掛一個有8根香蕉的香蕉串，然后要求Y根據數的組成與分解方法為猴子的另一只胳膊掛上合適的香蕉串。下面是干預過程中的實錄。

研究者：小猴子的一只手上拿了一串香蕉，你數數看這串香蕉一共有幾根？

Y：（開始點數）8根。

研究者：這串香蕉可沉了，小猴子一只手拿著，身子都歪了。請你在小猴子的另一只手上掛兩串香蕉，讓小猴子的身子保持平衡。試試看。

（Y在研究者事先準備的有1～7根香蕉的香蕉串中多次進行試誤選擇，通過操作判斷如何使兩邊一樣重。）

研究者：好的，現在小猴子的兩個肩膀平衡了（呈現KR.）。不過，剛才你是一串一串試的，你再看一看以前做“撒紐扣”游戲時的記錄單.想一想可以用什么方法讓小猴子的兩只肩膀一下子就平衡呢？

（Y沒有理解，仍用之前使用的試誤法。）

研究者：這個方法不對.這還是你剛才用過的辦法（呈現K1K）。請你看一看“撒紐扣”游戲的記錄單。8可以分成幾和幾？分出來的兩個數字合起來是不是就是8呢？我們來試試看。

研究者：（在Y面前擺了一個7根的香蕉串）需要8根香蕉.還缺多少？

Y：1根。

研究者：你把它們掛上去試試看。很好（呈現KR）！我們再試試其他方法。

（三）關于書面數符號的表征

書面數符號表征的干預主要滲透在“撒紐扣”和“猴子掛香蕉”兩個游戲中進行。“撒紐扣”游戲設計有記錄環節，要求Y用數字記錄每次拋撒紐扣的結果；“猴子掛香蕉”游戲中用的每一串香蕉上都有相應的數字，研究者請Y解釋這些數字所代表的含義，例如，“這個10表示這一串香蕉共有10根”。

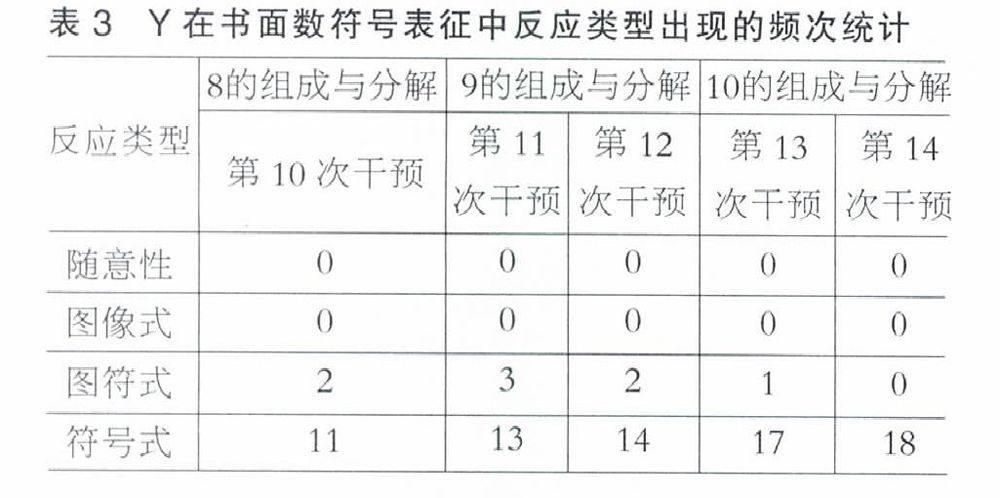
Hughes（1998）認為，兒童書面數符號表征一般有四種水平，即（1）隨意性反應，提指符號與數量無任何關系，如用涂鴉、畫畫或想象性文字等方式來表征；（2）圖像式反應，即符號既反映數量也反映實物特征，如用形狀、顏色或大小等來表征；（3）圖符式反應，即符號只反映數量，不反映物體特征，如用豎線、數點等來表征；（4）符號式反應，通常為用阿拉伯數字來表征。研究者對每次干預中Y出現的錯誤類型及頻次進行了詳細記錄。由表3可知，在最后難度較高的5次干預中，Y已基本掌握10以內的書面數符號表征，但表現不夠穩定。

（四）關于口頭加減運算

口頭加減運算能力的干預主要通過“加減飛行棋”游戲進行。游戲中，研究者請Y擲6面和10面的骰子并對數進行多種組合。游戲共設計有三個難度層次，每個難度層次進行一次游戲。每個難度層次成功后再進入下一層次。

盡管研究者前期對Y進行了數的組成與分解能力的干預，幫助他掌握了運用數的組合規律進行運算的方法，但Y仍傾向于運用數數的方法進行運算。在遇到數目較大的情況時，他更傾向于采用低層次的方法。㈣Y用數手指策略進行加法運算時，通常是從被加數開始計算的，如計算“3+11”時，先把11記在心里，然后伸出3個手指，逐一向上唱數“12、13、14”，求出和數：進行減法運算時則通常是從被減數開始計算的，如計算“10-3”時，會伸出3個手指，然后從10開始點數手指唱倒計數“9、8、7”，求出差數。由于不能直接得出正確答案，Y只能借助于計數的方式計算，從表4可以看出，Y的出錯率較高，表現較不穩定。

三、干預結果

總的來看，干預結束時，Y已能夠進行10以內數量的正確表征，但10以上數量表征的表現仍然不穩定；能夠較熟練地進行10以內的加減運算，但10以上的加減運算正確率較低，需要使用“數手指”策略；已熟練掌握6以內數字的組成與分解，但6以上數字組成與分解表現不穩定。

在對Y進行的TEMA后測中，Y所得的原始分為39分，能力分為105，與前測的原始分28分、能力分99分相比進步明顯。

四、討論與反思

（一）對Y數學學習困難成因的探討

1.認知因素

兒童數學認知障礙的形成原因不僅涉及諸如注意、理解、表征、記憶、推理、頓悟、抑制、轉換、遷移、策略、元認知等多項認知和心理過程因素，也涉及諸如焦慮、自我效能感等非認知因素，還和前額葉皮層等認知神經作用機制有關。研究者對Y的各項認知能力也進行了測查，結果表明，Y的視覺工作記憶得分為19分（M=20.37，SD=6.52）.言語工作記憶得分為16分（M=16.70，SD=3.71）。工作記憶得分為35分（M=37.08，SD=8.77）.執行功能總分為24.08分（M=15.91，SD=5.14）。這一測查結果告訴我們，Y除工作記憶能力略低之外，其他認知能力均高于平均值。由此可以推論，認知技能應該不是造成Y數學學習困難的主要原因。

2.學習品質因素

兒童在活動中表現出來的學習品質可從主動性、目標意識、堅持性、抗挫折能力、想像與創造性、專注程度、好奇心、獨立性等方面進行考察（王寶華、馮曉霞、肖樹娟等，2010）。從干預過程來看。Y學習缺乏主動性，不愿意參加活動，經常對研究者說“我一動腦子就煩”；Y的任務目標意識也一般，活動過程中常常會偏離目標，需經提醒后才會轉回。學習主動性、目標意識、堅持性、專注程度等都較欠缺，這可能是Y數學學習困難的主要原因。

3.幼兒園環境因素

幼兒園老師對Y數學能力的評價基本是負面的。這可能使Y對數學學習產生了畏懼心理，并降低了數學學習的自我效能感，進而不愿意參加相關的數學活動，形成惡性循環。因此，幼兒園消極的師幼互動可能是Y數學學習困難的影響因素之一。

4.家庭學習環境因素

有研究表明，家庭學習環境對兒童的學習與發展具有顯著的預測作用，它比父母受教育程度、家庭收入等影響都大。例如，父母與兒童能積極互動，如主動給孩子講解有關科學知識，經常帶孩子外出觀看電影、演出、體育比賽，父親積極參與孩子的家庭教育等，對兒童的入學準備有顯著影響。Y家庭學習環境中的物質因素（學習材料、書籍等）和精神因素（親子閱讀、游戲互動等）都不甚理想，他在日常生活中難以積累起足夠的數經驗，也無從談起獲得相應的數概念。這也可能是造成Y數學學習困難的原因之一。

（二）對干預過程與結果的反思

1.干預內容的全面性有待提高

受時間、精力限制，研究者對Y的干預偏重于狹義的兒童早期數學認知，包括數數、初步的數學運算以及對書面數符號的表征等內容，對兒童其他方面的數學認知能力，如空間方位、幾何圖形、測量、模式、排序等關注較少。換言之，干預內容的全面性有待進一步提高。

2.宜結合問題解決進行“數的組成與分解”的干預

有研究表明，兒童對個位數加減運算知識的記憶是一個較長的過程，一味強調速度，或要求兒童機械背誦答案會產生不良后果（Ginsburg，1989）。因此，Baroodv（1993）指出，要讓兒童運用一種問題解決的方法進行一種有目的的練習，從而促進兒童對數的組成與分解的理解。從這個角度反思，我們的“撒紐扣”游戲過于簡單機械，而“猴子掛香蕉”游戲因涉及數量守恒、交換律、互補原則等數學知識，對Y的認知挑戰難度可能過大，且兩個游戲并沒有提供一個真實的問題解決環境。因此，如何創設真實的問題情境進行干預，尚需作進一步的深入探討。

3.自我覺錯能力訓練是一種行之有效的干預策略

研究結果顯示，Y的覺錯能力較之前有所提高，表明干預對Y的數學能力發展有積極意義。另外仍有一些問題需作后續研究，例如，覺錯能力干預的強度多大為宜，需作多長時間的干預才能保證干預效果的穩定，以及干預成效如何盡快體現在兒童的學習中，等等。