變換群與若干哲學范疇的廣譜分析

郭少磊

（華北水利水電大學 水利學院，鄭州 450011）

【經管索微】

變換群與若干哲學范疇的廣譜分析

郭少磊

（華北水利水電大學 水利學院，鄭州 450011）

從廣譜哲學的視角出發，可把變換群看成人的一種觀控方式，從而把變換群、不變性與事物客觀性三者聯系起來；分析變換群與分類的內在聯系，可引出差異與同一、共性與個性的變換群描述；運用廣譜哲學的類變理論，可揭示變換群與量變質變規律、可推測與不可推測的數學機理。

變換群；哲學范疇；廣譜分析

通常對變換群概念的理解主要限定在純數學意義上，很少涉及到其事理和哲理。本文依據廣譜哲學對變換群概念和方法的分析，探討變換群與人的觀控方式和事物的客觀性，以及變換群誘導的差異與同一、共性與個性、量變與質變、可推測與不可推測等重要關系的意義。

一、變換群與觀控方式

變換群是以變換為元素的群，通常的抽象群是滿足4個條件（封閉性、結合性、單位元、逆元）的集合，但由于變換作為元素的特殊性，因此由變換構成群的條件僅需要2個。設G是變換的集合，*是變換之間的運算。若滿足：（1）G中任兩個變換的復合變換存在，且仍是G中的一個變換；（2）G中每個變換的逆變換存在，且仍是G中的一個變換；則（G，*）是一個變換群。

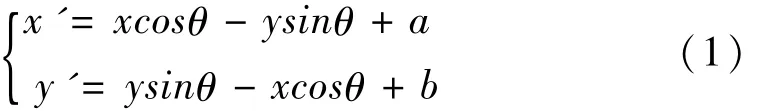
在廣譜哲學中，變換被看成一類特殊的觀控方式。［1］30－31觀控方式即人們觀察和控制事物的方式（角度、層次、方法、手段、條件等）。例如通常做實驗就是先控后觀，即把實驗對象置于一個典型環境下進行觀察。數學上的變換在操作意義上也表現為一定觀控方式下的觀察。例如解析幾何中的坐標變換可以看做先旋轉再平移的操作；給定一個幾何對象（如三角形、圓等），看它在上述操作下，哪些性質變化，哪些性質不變，這就是先控后觀的方式。此外，像仿射幾何中的仿射變換、射影幾何中的射影變換、拓撲學中的拓撲變換等，均可如是觀。在經典力學中，伽利略變換代表了宏觀低速條件下的觀察方式，而狹義相對論的洛倫茲變換，代表了微觀、高速條件下的觀控方式。［1］41－42此外，廣義相對論中任意參照系之間的變換、規范場論中的位相變換等，均有確切的觀控意義。

把變換群的元素（變換）視為一定觀控方式的觀點，將為分析一般事物的機理打開新的視野。

二、變換群與事物的客觀性

在廣譜哲學中，研究對象的客觀性被定義為：在一定的觀控條件下，n個人或n次（n在理論上可以為無窮大）獨立的觀控結果具有一致性或不變性。進一步簡化、抽象后，客觀性即一定觀控方式下n重觀控結果的等價性。［1］當變換群的元素即變換被看成是一定的觀控方式時，則變換群下的不變性便與研究對象的客觀性聯系起來了。例如，由形如（1）的所有變換構成一個變換群，稱為運動群。容易驗證，在變換（1）的作用下，一個平面圖形的長度、角度均不變，因此該幾何圖形的形狀和大小均保持不變。換言之，在旋轉和平移的操作下，物體（這里是幾何圖形）的剛性不變。

這時，剛性就是旋轉平移這種觀控方式下的客觀屬性。又如伽利略變換構成一個變換群，稱為伽利略變換群。不難驗證，在伽利略變換下，時間間隔，空間間隔 （一物體的長度）以及牛頓力學定律都是不變的。換言之，在伽利略變換（反映宏觀低速運動）這種觀控方式下，時間不變、空間不變是自然界物質運動的客觀屬性，牛頓力學定律（如）是自然界物質運動的客觀規律。同樣，洛倫茲變換也構成一個變換群，稱為洛倫茲變換群。可以證明，在洛倫茲變換下，上述的時間間隔、空間間隔要改變，但時空間隔不變，它反映了在洛倫茲變換（反映微觀高速運動）這種觀控方式下，時空相互聯系的屬性是一個客觀屬性。此外還可以證明，在洛倫茲變換下，在不同的慣性系，麥克斯韋方程組的形式是不變的，它反映了高速運動（電磁場運動）下電磁場規律的客觀性。

把變換群、不變性、客觀性這三個表面上不相關的概念聯系起來，我們就能在科學觀上得到一個深化：既然變換群下的不變性反映了事物的客觀性，而一切科學都是研究一定事物一定層面的客觀性的，因此，一切科學都是研究一定觀控方式下一定事物一定層面的不變性的。［2］顯然，這一結論給我們提供了透視各門科學的一個重要側面。

三、由變換群誘導的若干重要關系

在數學上可以證明，給定集合X上的一個變換群G，可以誘導一個等價關系，從而決定了X的一個分類；反之，給定X上的一個分類，可以誘導X上的一個變換群G，即分類與變換群有著緊密的內在聯系。［3］由這種聯系，我們可以引出對認識論、本體論有重要價值的若干關系的廣義量化模型。

（一）差異與同一的關系。

按照廣譜哲學的觀點，等價關系作為分類標準，也反映了一定的觀控水平。例如，設A是人的集合，按“同性別關系”（等價關系），可以把A分成“男人類”和“女人類”；按照“同品德關系”（等價關系），可以把A分成“好人類”和“壞人類”，等等。顯然，從性別上和品德上看人，代表兩種不同的觀控水平。當我們選定一種觀控水平時，一個集合A就被分成若干個等價類，在同一個等價類內，所有的事物在等價關系（同一性關系）［4］的意義上視為無差別。但在不同的等價類之間，分處兩個等價類的事物，視為有質的差別，這就引出了差異與同一的關系。

從數學上看，分類是一個映射fδ：→A／δ，其中A／δ＝｛A1｜i＝1，2…，n｝，且當i≠j時，A1∩AJ＝Φ（空集）。這時，所謂同一性是指，對?x，y∈Ai，有（x，y）。所謂差異性是指，對?x∈Ai，y∈Aj（i≠j），有（x，y）∈Ai×Aj，其中符號×表示笛卡爾直積。

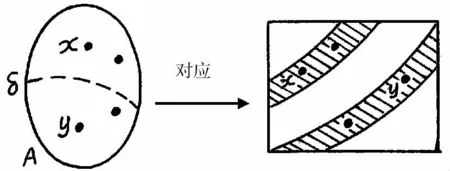
圖1 等價類對應變換群的軌道

上面講的變換群可以誘導一個等價關系，實質上是說，對于集合A的任兩個元素x，y∈A，變換群的一個變換g∈G，把x變成y，即g（x）＝y，而這樣一個關系是一個等價關系。原因在于變換群有恒等變換I∈G，它把任意的x∈A，變成x自身，即g（x）＝x，這就導致自返性。其次，變換群的每個變換g∈G，存在逆變換g－1，使得當g（x）＝y時，有g－1（y）＝x，這就導致對稱性。最后，由變換的復合可導致傳遞性。這就誘導了一個等價關系。通常把集合Ωx＝｛g（x）｜g∈G，x∈A｝稱為A在G作用下的軌道。容易知道，變換群作用在集合A上的效果是：它把由δ劃分的每一類元素變成自己一類的元素，因此，變換群作用下的每一條軌道恰好是由δ劃分出來的一個等價類（圖1）。于是同一性與差異性轉化成變換群的語言，這時所謂同一性是指，對?x，y∈Ωx，有（x，y）∈；而差異性是指，對?x∈Ωx，y∈Ωy，有（x，y）∈Ωx×Ωy，即同一條軌道上的兩個事物具有同一性，不同軌道上的事物具有差異性。

（二）共性與個性的關系

當等價關系選定后，分類也可以從共性和個性的角度進行分析。不同等價類內的事物，在不具有等價關系的意義上沒有共性。例如男人類和女人類各取一個元素，在不具有同性別的意義上，沒有共性（雖然具有一般人的共性，那是另一種分類標準）。但在同一個等價類里，（x，y）∈A2（A1∈A／δ），它們在等價關系的意義上具有共性。這時任何x，y∈A1，有x≠y，這是各個事物的個性或特殊性。例如在男人類里，任何兩個男人在長相、身高、膚色、體態等方面是各個不同的。顯然，把等價類看成是變換群的軌道，有類似的結論。不過，用變換群的軌道描述共性和個性，更適于描述同一個事物的變化過程，即一個事物由x態變到x＇態時，如果處在同一條軌道上，它們具有共性，但x≠x＇，又具有各自的特殊性。這就如同處在同一圓（旋轉群的一條軌道）上的兩點x和x＇，它們具有相同的半徑（共性），但它們位置不同（特殊性或個性）。

（三）量變與質變的關系

如果考慮事物自身的發展變化可以劃分為若干個階段，則劃分的標準成為沿時間方向展開的等價關系（廣譜哲學稱為自等價關系），它的實質是在一定時段內“保持事物的性質不變”。例如，水在0℃到100℃之間保持液態水不變，就是廣義的量變，廣譜哲學稱為同類變，即在同一個等價類內的變化。但當達到100℃時，液態水變成汽態水，就是廣義的質變，廣譜哲學稱為異類變，［2－5］即從一個自等價類躍遷到了另一個自等價類。

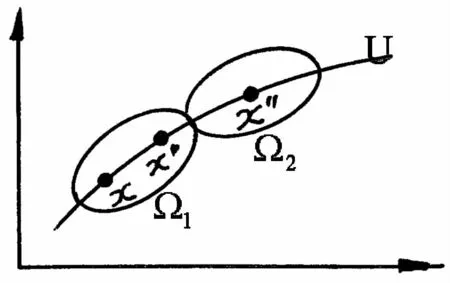
圖2 從變換群軌道上看量變和質變關系

從變換群的角度看，上述按自等價關系的分類也對應一個變換群，稱為自等價變換群，這個變換群的軌道生成諸自等價類。在圖2中，（（x，1），（x＇，t＇））∈是在同一條軌道內變化，即廣義的量變，而（（x，t），（x＇，t＇））∈Ω1×Ω2是從一條軌道Ω1躍遷到了另一條軌道Ω2，即廣義的質變。［2］

一個典型的例子是社會上的等級現象（權力等級、職稱等級、學歷等級等），可以看成一種劃分，其等價關系是“處在同一等級中”，這時每個等級是一個等價類，從而對應變換群的一條軌道。當一個人沒有得到提升，始終處在同一個等級時，表現在同一條軌道上“滑行”（如從一個科級崗移到另一個科級崗），這是廣義的量變。當他得到了提升，從一個較低的軌道躍遷到較高的軌道，或者他被降級，從較高的軌道躍遷到較低的軌道，就是廣義的質變，如圖3所示。

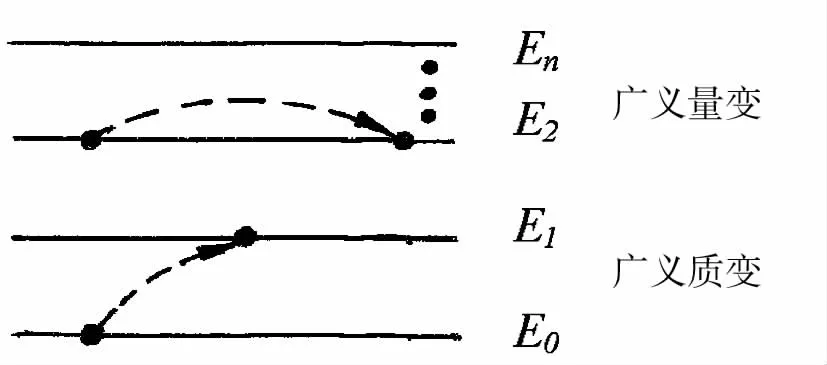
圖3 等級現象中的量變和質變

（四）可推測與不可推測的關系

從認識論角度看，上述量變質變模型可用來研究人們如何推斷過去和預測未來。推斷過去是從現在推測過去，即“向后看”，預測未來是從現在推測將來，即“向前看”。廣譜哲學認為，無論“向后看”還是“向前看”都要依據某種不變性（不變的性狀或規律），稱為“等價遷移條件”。［1］在圖2中，由于（（x，t），（x＇，t＇））∈即t時刻x的性狀與t＇時刻x＇的性狀沒有本質差別（處在同一條軌道即同一個等價類中），因此，可以從（x＇，t＇）的性狀推出（x，t）的性狀，反之亦然。例如，可以從人造地球衛星現在的位置（x＇，t＇）推出以前某時刻的位置（x，t），也可以從現在的位置（x，t）推出未來某時刻的位置（x＇，t＇）。其原因在于衛星處在同一條軌道（等價類）上。如果衛星突然變軌就無法做上述推測，這是因為等價遷移的條件遭到了破壞。

一般說，當事物的變化處在變換群的同一條軌道（同一個等價類內）時，可以依據不變性推斷過去和預測未來，當事物的變化是由一條軌道躍遷到另一條軌道時，由于兩條軌道之間不存在變換（注意前面講的變換群把由δ劃分的每一類元素變成自己一類的元素），因此上述推斷與預測就不可能了。

不過，換個角度看，不可推測是由分類造成的。如果分類標準變了，則等價類的劃分也變了，從而變換群的軌道也變了，如圖4所示。

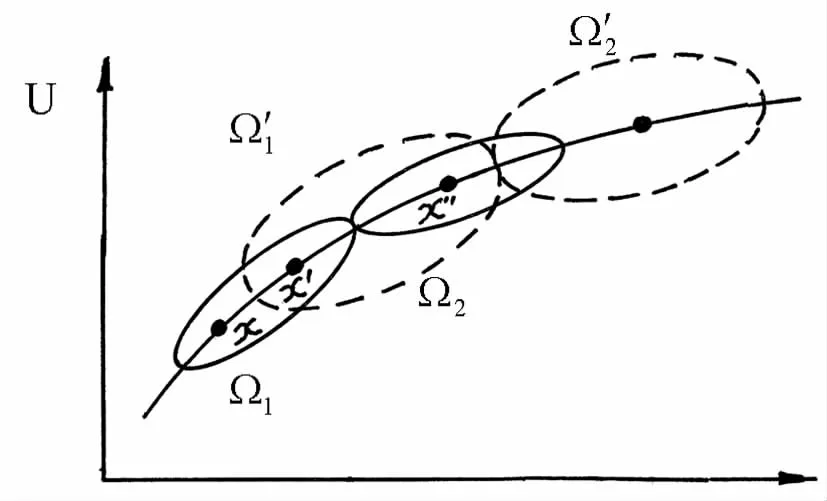
圖4 從變換群軌道看可推測與不可推測關系

圖4中，對于原軌道Ω1和Ω2而言，由于（（x，t），（x＇，t＇））∈，故從（x，t）到（x＇，t＇）或者反過來是可推測的。但由于（（x，t），（x＇，t＇））∈Ω1×Ω2，故從（x，t）到（x＇，t＇）或者反過來不可推測。對于新軌道Ω＇1和Ω＇2而言，由于（（x＇，t＇），（x＇，t＇））∈，因此由（x＇，t＇）到（x＇，t＇）或者反過來是可推測的（注意對舊軌道不可推測）。這就是說，當分類標準改變時，可推測與不可推測具有相對性。

例如，我們從監控錄相中鎖定了犯罪嫌疑人的相貌特征。一般情況下，人的相貌特征在一定時段內是穩定不變的，可以看成在一個自等價類中。但若該犯罪嫌疑人做了重大的整容手術，則破壞了等價遷移條件，就無法推斷該犯罪嫌疑人以前的相貌特征。不過，如果還提取了犯罪嫌疑人的DNA結構，由于DNA結構不會隨相貌的改變而改變，它會在很長的時段（生前乃至死后）保持同構性（一種等價關系），因此可推斷“此犯罪嫌疑人就是彼犯罪嫌疑人”。

四、結語

綜上所論，變換群的概念經過結構分析（它與分類的聯系），事理分析（它與觀控方式、客觀性的聯系），哲理分析（它與異同關系、共性個性關系、量變質變關系、可推測與不可推測關系等的內在關聯），展現了極深刻的內涵和廣泛的意義。當把它的精髓概括為一定觀控下的不變性時，它已不限于是一個純數學的概念，而是成為我們觀察現實、分析現實的一種重要的觀控方式。

［1］張玉祥.廣譜存在論導引［M］.香港：香港天馬出版有限公司，2004.

［2］張玉祥.廣譜哲學在自然辯證法教學中的若干應用［J］.華北水利水電學院學報：社會科學版，2009，（1）：17－20.

［3］張堯庭.指標量化、序化的理論和方法［M］.北京：科學出版社，1999：41－43.

［4］張玉祥.結構型數學及其在廣譜分析中的應用［J］.河南科學，2009，（5）：525－529.

［5］王曉崗.關于哲學數學化的一些思考——從廣譜哲學談起［J］.廣西社會科學，2012，（9）：32－35.

A Broad-spectrum Analysis on Transformation Group and Philosophical Catetories

GUO Shao-lei

（School of Water Conservancy，North China University of Water Conservancy and Hydroelectric Power，Zhengzhou 450011，China）

Based on broad-spectrum philosophy，transformation group is taken as ahuman observocontrol mode which connects transformation group with invariance and objectivity.An analysis on ingenerate connection between transformation group and classification makes expression of transformation group in terms of difference and identity，generality and individuality clear.The Class-change theory of broad-spectrum philosophy can reveal both the relationships between transformation group and qualitative and quantitative change and the mathematical mechanism of reference and non-reference.

transformation group；philosophical categories；broad-spectrum analysis

C02

：A

：1672－3910（2013）05－0084－04

2013－05－29

郭少磊（1982－），男，河北元氏人，北京林業大學博士生。