無線通信網絡中的M/G/1重試排隊模型

周宗好，石志巖

（1.黃山學院數學與統計學院，安徽黃山245041；2.江蘇大學理學院，江蘇鎮江212013）

無線通信網絡中的M/G/1重試排隊模型

周宗好1，石志巖2

（1.黃山學院數學與統計學院，安徽黃山245041；2.江蘇大學理學院，江蘇鎮江212013）

為了使無線網絡的節點盡可能的節約電能，本文討論睡眠喚醒機制下網絡節點的動態排隊.當無線網絡節點中緩存隊列變空時，節點即不發送也不接收數據包并且進入一段隨機長度的休假期.為了使模型具有更一般的適用性，考慮節點對數據包傳輸時間分布為一般分布.基于上述要求本文研究了帶有空竭服務的單重休假、一般重試時間的M/G/1排隊系統，求得系統穩態存在的充分必要條件.利用向量馬氏過程(VMP)的方法求得系統的各項排隊指標.求解的結論可用于優化無線通信網絡的各項性能指標.

無線通信網絡；穩態分布；馬氏鏈；空竭服務

1引言

無線網絡節點對電能的需求也在不斷地提高，因此采用有效的功率管理(powermanagement)機制使節點降低能耗是無線網絡設計首先需要考慮的因素[1].另外，作為無線網絡的另一個重要因素，網絡的QoS也必須得到有效的保障，降低網絡節點能耗和保障網絡QoS的折衷問題已經成為近幾年無線網絡中的研究熱點之一，本文就無線通信網絡中的排隊系統在工作中節點常因無數據傳輸而休假[2]；常因為了節省資源而具有空竭服務[3-4]；也就是筆者考慮的帶有空竭服務的M/G/1排隊模型.

2模型描述

無線網絡節點可視為排隊系統的服務臺，它負責傳送到達的數據流.節點工作在兩種狀態：活動(active)狀態和睡眠(sleep)狀態.在活動狀態，節點具有較高的能耗，處于此狀態的網絡節點主要工作在三個階段：傳輸期、空閑期和休假期，其中傳輸期和空閑期為活動狀態，并作假設：

數據包到達服從參數為λ的Poisson流，數據包到達受阻則離開服務區域進入無限位置的重試軌道(orbit)，并且按照FCFS規則排隊等待.系統服務完一個數據包后，若orbit中沒有數據包則系統直接進入休假期，即空竭服務規則.重試時間間隔和數據包的服務時間、處理器休假時間都服從一般分布函數A(x)、B(x)和V(x)；它們的密度函數、拉普拉斯司梯階變換(LST)、一階矩及二階矩分別為統只有在服務時間里才發生故障，失效率為μ，數據包已經服務過的時間有效.假定數據包的到達時間間隔、服務時間、處理器的休假時間分布相互獨立.

設C(t)=i表示節點所處的狀態(i=0,1,2,分別表示在時刻t節點處于空閑、服務和休假期)；N(t)表示在時刻t在orbit中的數據包數；當C(t)=0且N(t)>0時，ξi(t)(i=0,1,2)分別表示在時刻t逝去的重試、服務和休假時間.馬爾可夫過程的狀態空間為：

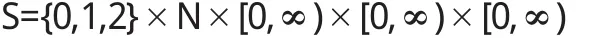
令a(x),b(x),v(x)分別表示在時刻t重試、服務和休假的風險率函數，即有：

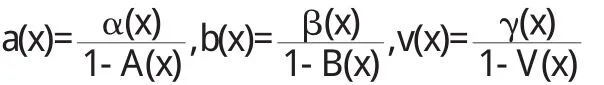
3穩態條件分析

系統的到達過程為Poisson流，由Burke定理知馬爾可夫過程C(t),N(t),ξ0(t),ξ1(t),ξ2(t)}的穩態概率分布存在當且僅當

4 模型求解及相關指標

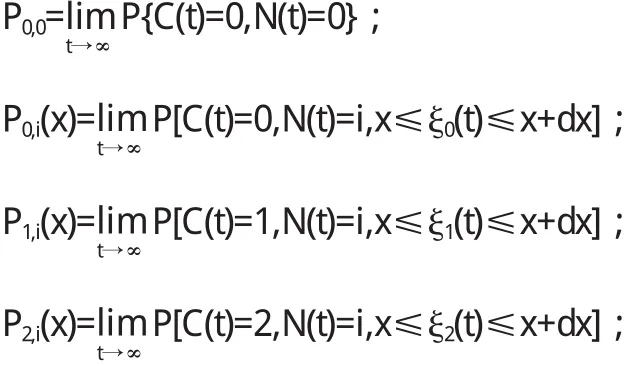
t≥0,i≥0,x≥0.

由補充變量法可得系統穩態的微分方程組：

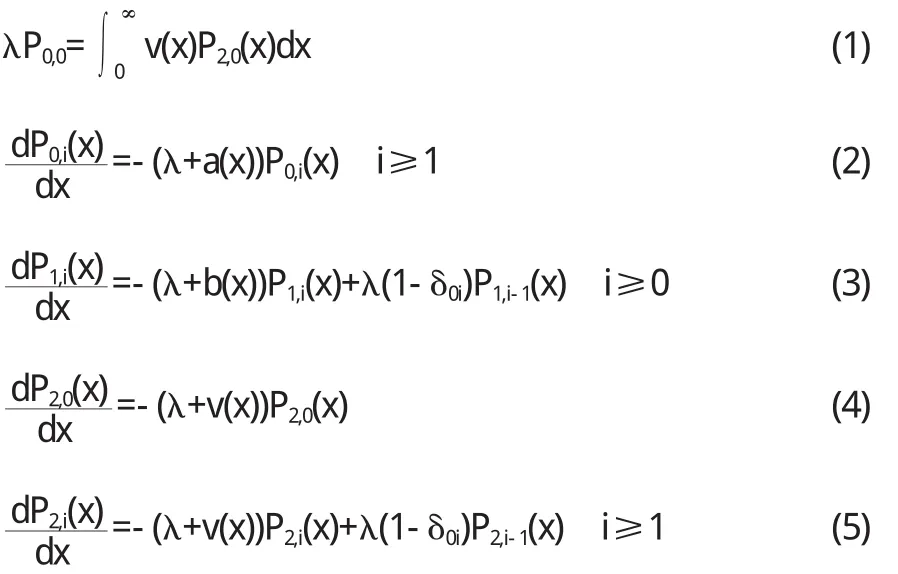
邊界條件為：

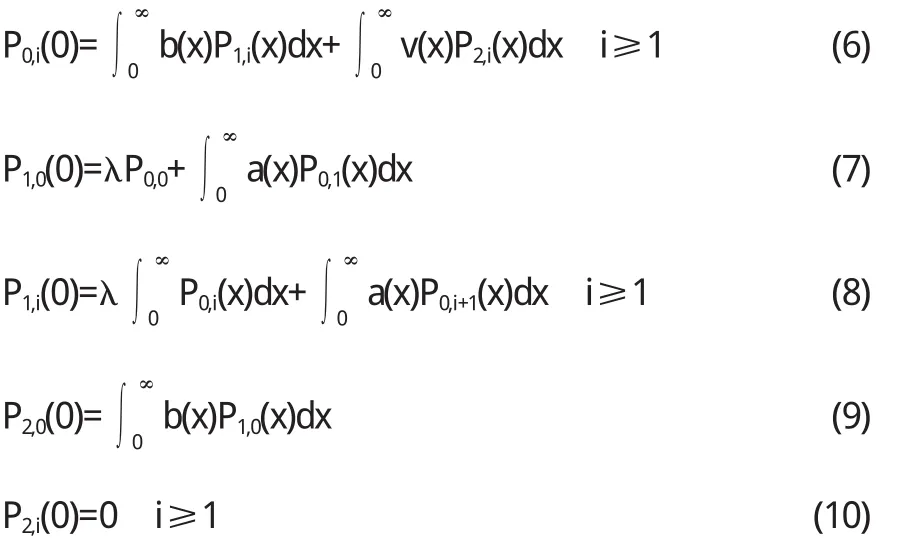
正則性條件：

利用上面的（1）-（11）式，討論系統的穩態分布,令：

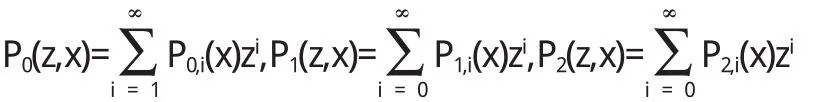
把上面微分方程(1)-(10)取概率母函數，并把i從0到∞求和得:

由(16)-(18)得：

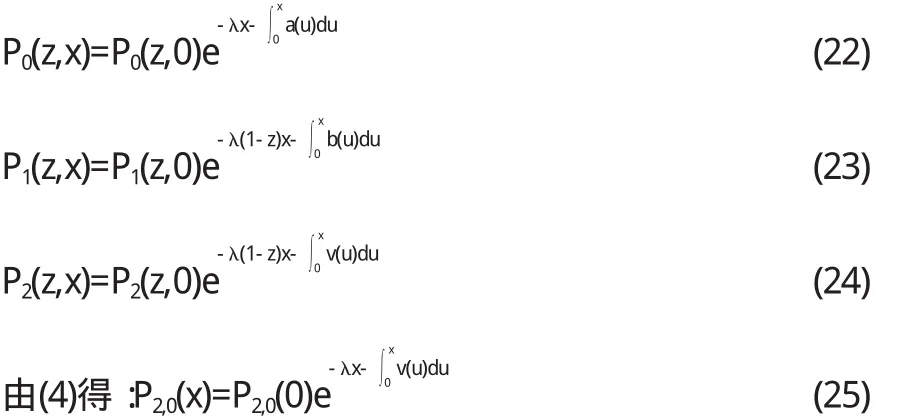
把(25)乘以v(x)，并從0到∞積分，考慮(1)式得：

由(21)知：

把(22)代入(20)式得：

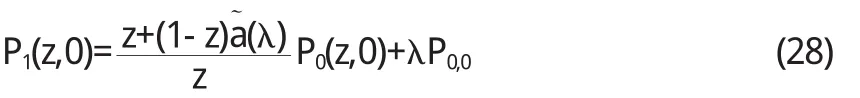
把(23)、(28)、(24)、(27)式代入(19)式,同時考慮(21)與(26)式得：

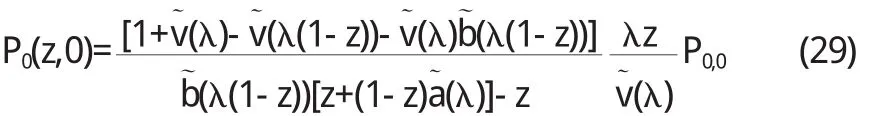
把(29)式代入(28)式整理得：

再把(29)、(30)、(27)式代入(22)-(24)式可得：

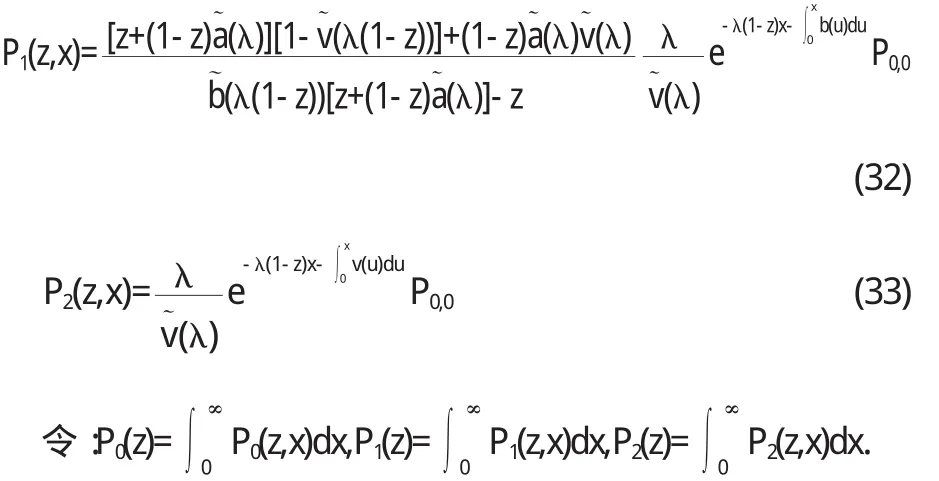
運用LH0spital法則和正則性條件：P0,0+P0(1)+P1(1)+P2(1) =1經整理得：

5 排隊指標

根據以上求得的概率母函數可以求得一下結論：

（1）節點處于空閑、服務與休假期的概率分別為：

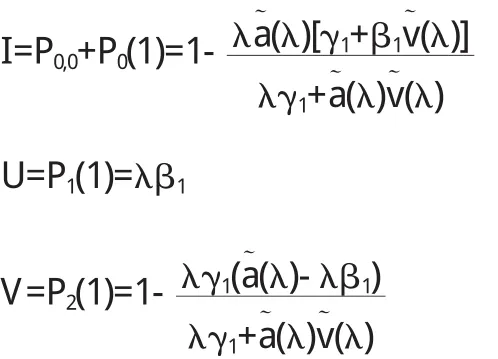
（2）系統中數據包數、orbit中的數據包數的概率母函數分別是：

進一步可得系統的平均數據包數和orbit中隊列的平均數據包數分別為：

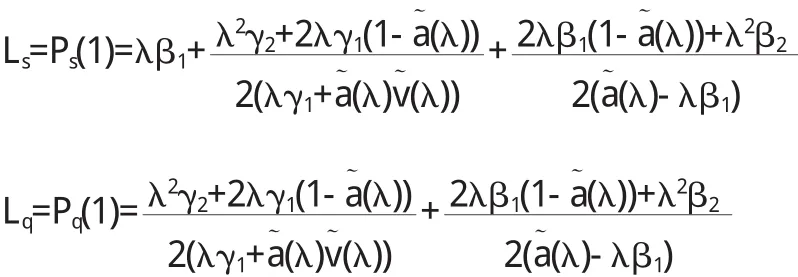
（3）系統中的數據包平均等待時間與平均逗留時間分別為：

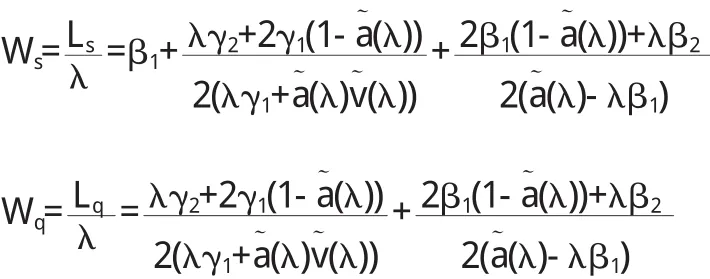
6 結束語

本文針對無線通信網絡的數據包服務時間為一般分布的M/G/1型排隊模型進行了求解，該模型概括了服務時間是定長分布、指數分布及Erlang分布的特殊情況，從而使其具有普遍的適用性.模型還進一步考慮了無線通信網絡的數據包的重試傳輸、節能空竭服務與休假策略，因此模型的結論具有重要的應用價值.

〔1〕KrishnaKB,Arivudainambi,TheM/G/1Retrial QueuewithBernoulliVacationGeneralRetrialTimes [J],ComputersandMathematics.2002,43(1-2):15-30.

〔2〕周宗好,朱翼雋,馮艷剛.具有Bernoulli休假的M/G/1重試可修排隊系統[J].運籌學學報,2008,12(1):71-82.

〔3〕朱翼雋,周宗好,馮艷剛.具有優先權的M/G/1重試可修排隊系統[J].自動化學報,2008,34(2):195-201.

〔4〕MorenoP,AnM/G/1retrialtimewithrecurrentcustomersandgeneralretrialtimes[J],AppliedMathematics andComputation,2004,159(3):651-666.

〔5〕KrishnaKB,PavaiMS,VijayakumarA,TheM/G/1 retrialqueuewithfeedbackandstartingfailures[J], AppliedMathematicalModelling,2002,26(11):1057-1075.

〔6〕AtenciaI.,MorenoP,Asingle-serverretrialqueue withgeneralretrialtimesandBernoulliSchedule[J], AppliedMathematicsandComputation,2005,162(2): 855-880.

〔7〕TakacsL.Introductiontothetheoryofqueues[M], NewYork:OxfordUniversityPress,1962:1-355.

O226

A

1673-260X（2013）06-0001-03

國家自然科學基金資助項目(11226210)；安徽省高校省級自然科學研究項目(KJ2013B272)；黃山學院科研啟動項目(2012xkjq008)