基于ADF檢驗的中國出口集裝箱班輪運價隨機特性研究＊

陳麗江

（1．上海海事大學 經濟管理學院，上海201306；2．上海財經大學 統計與管理學院，上海200433）

金融市場的研究往往會涉及到價格時間序列是否服從隨機游走特性，并以此來判斷市場的有效性。美國經濟學家Fama將有效市場分為弱式有效、半強式有效和強式有效3種，其中檢驗弱式有效市場的方法之一就是通過檢驗價格是否服從隨機游走，來檢驗價格對信息流反應的靈敏度變化的影響［1］。最新的金融市場有效性研究都是采用不同的數學方法和數據頻率來分析，因而對市場的隨機游走行為有不同的見解，常見的隨機游走的檢驗方法有單位根檢驗，如自相關檢驗、DF檢驗、ADF檢驗、方差比檢驗等。

許多專家學者采用各種方法檢驗了航運價格的隨機特性，但結論不盡相同：Hawdon模擬了油品運價的波動路徑，研究發現其具有均值回復的特征［2］。Berg－Andreassen用單位根檢驗法檢驗了干散貨市場1985年4月至1988年12月的日觀測的BFI數據，他認為BFI序列有隨機游走的特征，即干散貨市場的運價呈現出非平穩特征，但一階差分后可達到平穩［3］。Glen和Rogers檢驗了好望角型航運市場的運費率，認為所有航線的運費率均為非平穩，但一階差分后可達到平穩［4］。Kavussanos檢驗了BIFFEX期貨價格的無偏，獲得其為隨機游走的結論［5］。M．G．Kavussanos和A．H．Alizadeh經研究認為，船舶市場價在理性預期的假設下市場有效性不成立，還用GARCH－M模型進行了分析［6］。李序穎對中國出口集裝箱運價指數（CCFI）與波羅的海干散貨運價指數（BDI）的基本統計特征進行對比分析，利用協整理論及Granger因果檢驗研究了兩者的關系，并對其收益序列及其波幅進行建模。研究發現，CCFI以及BDI收益序列具有股票價格收益序列的特征，CCFI與BDI具有協整關系，而且CCFI周收益率是BDI周收益率的Granger原因［7］。李耀鼎、宗蓓華運用迪克－富勒檢驗（augmented Dickey－Fuller，ADF）對波羅的海運價指數的對數序列進行檢驗，結果證明BDI對數序列是一個單位根過程，是非平穩的，但一階差分后是平穩過程，即BDI對數序列是一階單整的［8］。陸從克通過對國際干散貨航運市場中波羅的海好望角型船市場運價指數（baltic capesize index，BCI）序列以及對數收益率序列的平穩性、異方差性進行分析和檢驗，驗證了BCI半月對數序列存在單位根，是非平穩序列，服從隨機游走的假設［9］。范永輝、楊華龍、張寶華運用灰色關聯理論對近期波羅的海油輪運價指數和前2個月的布倫特現貨原油離岸價格之間的相關性進行研究，發現近期油輪運價指數波動滯后原油價格波動約3周左右［10］。

盡管許多專家對航運市場海運價格進行了研究，但大多數都是集中在近似完全競爭的干散貨市場，對于寡頭競爭的集裝箱班輪運輸市場運價隨機波動行為模式的研究尚未有公認的結論。

《2011年中國航運發展報告》顯示，2011年全國港口完成貨物吞吐量100．41億噸，外貿貨物吞吐量27．86億噸，集裝箱吞吐量1．64億TEU，分別比 上 年 增 長 12．4%、11．4% 和 12．0%［11］。2011年，僅上海港集裝箱吞吐量就突破了3 000萬TEU［12］。中國出口集裝箱運價指數（China containerized freight index，CCFI）由上海航運交易所發布，初始發布日是1998年4月，它是全球唯一的集裝箱班輪運價指數，經過14年的觀察發現，中國國際集裝箱班輪運輸市場的“陰晴”變化和運價走勢能夠在CCFI中得到較為迅速、客觀的反映。本文對中國出口集裝箱班輪運價的隨機特性進行了研究，以CCFI指數作為班輪運價的測度。

一、隨機游走及其檢驗

（一）隨機游走

若時間序列｛yt｝滿足

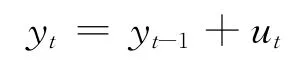
式中：p0為一個實數，它表示這個過程的起始值，｛ut｝是一個白噪聲序列即ut～ⅡD（0，σ2），則稱｛yt｝為一個隨機游動。

帶漂移的隨機游走序列為：yt＝μ＋yt－1＋ut，ut～ⅡD（0，σ2）；

帶趨勢項的隨機游走序列為：yt＝μ＋βt＋yt－1＋ut，ut～ⅡD（0，σ2）

（二）單位根檢驗

考慮一階自回歸過程AR（1）：

式（1）兩端同時減去yt－1，得到

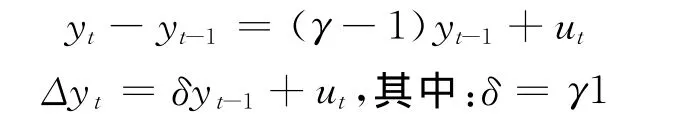
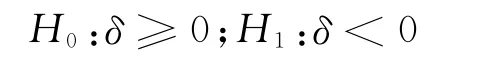
考慮到絕大多數經濟時間序列中yt－1的系數δ幾乎總為正值，于是假設δ＞0，前面的原假設和備擇假設可以寫成如下形式在δ＝0（或γ＝1）的情況下，即原假設若為真，則相應的過程是隨機游走過程，是非平穩的。可用以下的t統計檢驗量進行檢驗：

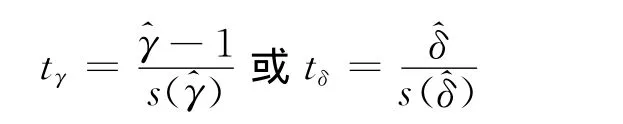
式中：s（＾γ）和s（＾δ）分別 為 參 數估 計 值＾γ 和＾δ 的 標準誤差。

迪克（Dickey）和福勒（Fuller）編制了tδ的臨界值表，即DF檢驗表，統計量稱之為τ統計量。DF檢驗中如果隨機誤差項具有自相關性，則可以通過增加變量的滯后項來消除殘差的自相關性，這由擴展的迪克－福勒檢驗（augmented Dickey－Fuller test，ADI）來實現。

ADF檢驗是這樣實現的：在給定的顯著性水平下查τ臨界值表，若tδ＜τ，則拒絕原假設H0，認為yt序列平穩；否則，若tδ＞τ，則接受原假設H0，認為yt序列有單位根，是非平穩的隨機游走序列。ADF檢驗的模型有3個，在進行ADF檢驗時，一般先從模型（3）開始檢驗，如果在給定的顯著性水平下發現β＝0，再擬合模型（2），在給定的顯著性水平下若常數項μ＝0，則要用模型（1）進行檢驗。

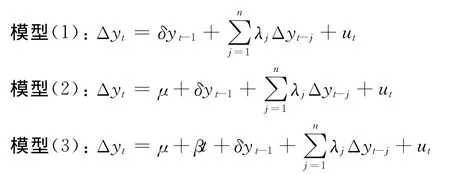
二、數據的預處理

在CCFI的編制中根據地區代表性、分布性、一致性原則來選擇樣本航線，具體有日本航線、香港航線、韓國航線、東南亞航線、澳新航線、歐洲航線、美西航線、美東航線、地中海航線、南非南美航線、東西非航線等11條航線，其國內出發港分別為大連、天津、青島、上海、南京、寧波、廈門、福州、深圳、廣州。本文研究采用中國出口集裝箱運價指數作為研究對象，采集了1998年至2011年每周發布的CCFI，數據來源于《航運交易公報》、上海航交所和國際航運研究中心Clarkson數據庫，每條航線周指數為733期。

值得一提的是，從2011年12月9日開始，CCFI的樣本航線新增了3條，原南非南美航線拆分為兩條南非航線、南美航線單獨計入樣本，又新增了波紅航線和臺灣航線計入樣本，因此，樣本航線變為14條。而且CCFI一般每周五發布，但是在發布的初期，發布時間并不一定在周五，盡管正式發布是在1998年4月，但是1998年1月至3月的數據也有公布在《航運交易公報》上。有時逢周五是公共節假日會停止發布，為了保持時間序列的可比性，本章對數據作了以下處理。

第一，對11條分航線的運價指數分別檢驗其隨機游走特性，不對中國出口集裝箱運價綜合指數進行單獨研究；第二，以“就近”的原則對數據的時間進行調整，將記載的CCFI都登記在周五，非周五發布的指數就登記時間為最近的那個周五；第三，如果逢節假日或者其它原因出現缺失值，則采用前后兩期的平均值來作為該期數據；第四，2011年12月9日之后的數據中，南非南美航線還是作為同一條航線，其運價指數采用南非航線和南美航線的均值；第五，不對新增的波紅航線和臺灣航線進行研究。

三、集裝箱班輪運價指數的ADF檢驗

為了鑒別中國國際集裝箱班輪運輸市場的運價波動的情況，本節將1998年－2011年11條航線的CCFI指數依次分成1年期至14年期，對其情況一一進行ADF檢驗，看其是否服從隨機游走。經過多次檢驗發現，不同的航線其隨機游走的時間長短不一樣，給定顯著性水平為α＝0．10，以下將檢驗的結果分成3類來分別說明。

（一）第一類：運價序列隨機游走時長在兩年以內

日本航線、澳新航線、韓國航線、東西非航線CCFI短期時間序列線形圖，見圖1。

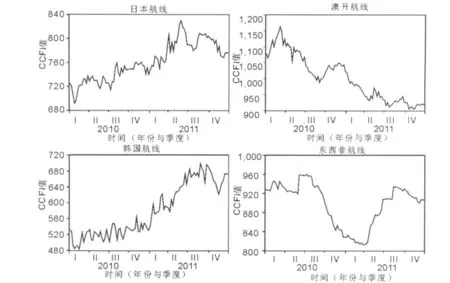
圖1 日本、澳新、韓國、東西非航線短期波動圖

由圖1可見這些序列都具有較為明顯的不平穩特征，且除了東南亞航線外，其余3條航線具有明顯趨勢。見表1。

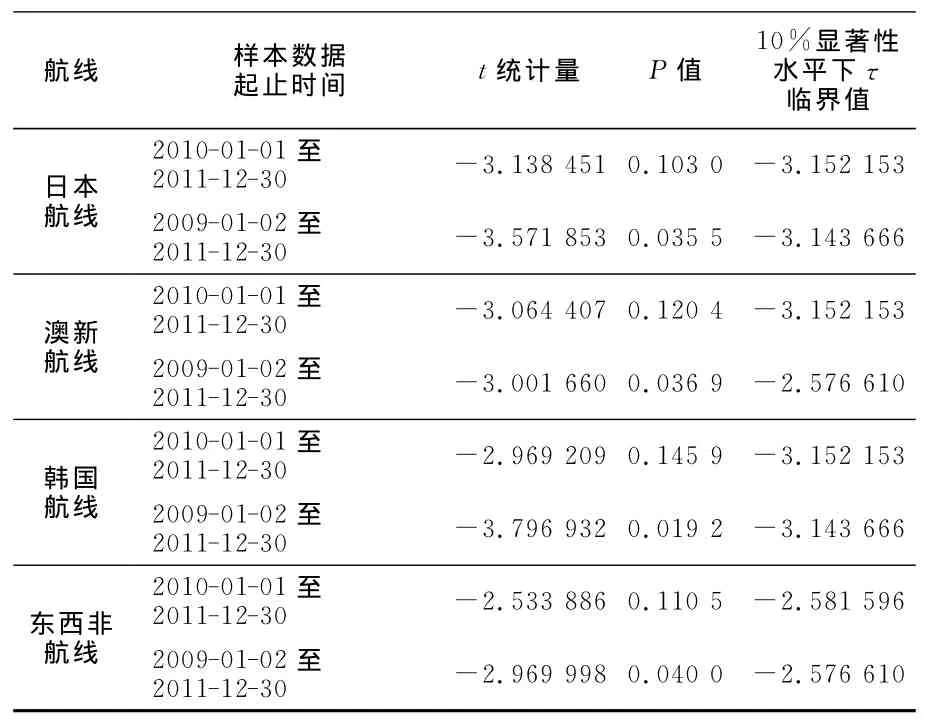
表1 日本、澳新、韓國和東西非航線指數的ADF檢驗

經過檢驗發現，在α＝0．05的顯著性水平下，日本航線、澳新航線、韓國航線、東西非航線這4條中國國際集裝箱班輪航線運價指數兩年及兩年以內的運價指數數據不能拒絕原假設即有單位根，即兩年及以內的指數時間序列為隨機游走序列；3年及3年以上運價指數數據經ADF檢驗結果為拒絕原假設，即3年及以上的指數時間序列是平穩的，服從均值回歸。

（二）第二類：運價序列隨機游走時長在10年以內

與第一類航線相似，東南亞航線、南非南美航線、美東航線和地中海航線短期的時間序列也具有比較明顯的隨機游走特征，除地中海航線具有比較明顯的趨勢外，其它3條航線的趨勢都不是很明顯。經過對歷年數據的ADF檢驗發現，在α＝0．1的顯著性水平下，東南亞航線和南非南美航線運價指數3年及以內指數時間序列為隨機游走序列，4年及以上運價指數序列是平穩的；美東航線運價指數序列5年及以內為隨機游走，6年及以上為平穩；地中海航線9年及以內為隨機游走，10年及以上為平穩。見表2。

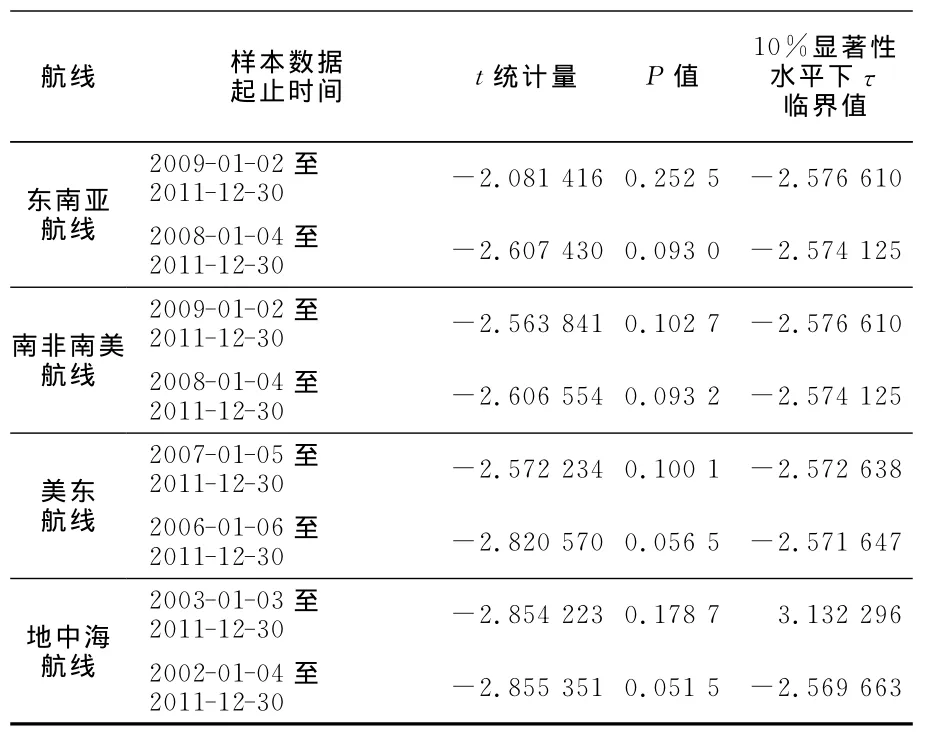
表2 東南亞、南非南美、美東和地中海航線指數的ADF檢驗

（三）第三類：運價序列隨機游走時間達10年以上

同樣可以觀察到歐洲航線、香港航線、美西航線的短期時間序列也具有明顯的隨機游走特征，且具有較為明顯的趨勢。對這3條航線的運價指數的歷年數據進行ADF檢驗還發現，在α＝0．1的顯著性水平下，歐洲航線、香港航線、美西航線運價指數在10年以內的數據均表現出明顯的隨機游走特征，檢驗結果均不能拒絕隨機游走的假設；隨著時間跨度的增加，運價指數時間序列的隨機游走特性慢慢減弱，均值回歸的特性逐漸增強，基本要13年以上才逐漸平穩，成為均值回歸。見表3、表4。

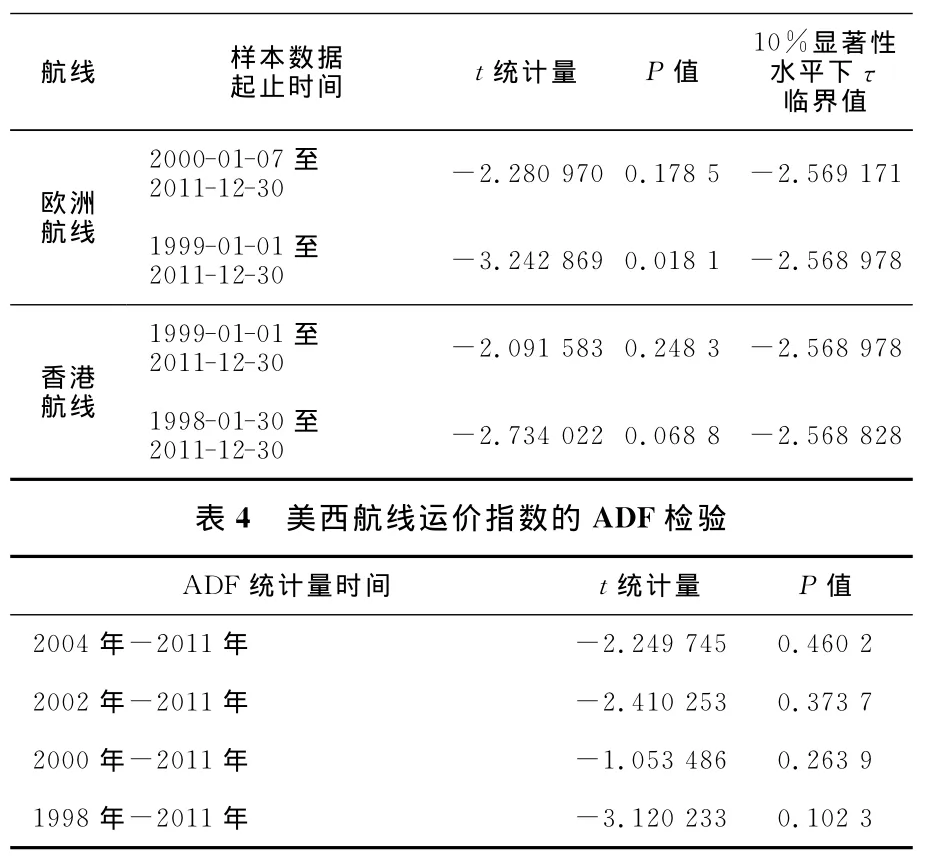
表3 歐洲和香港航線指數的ADF檢驗

四、模型的診斷和檢驗

以上對中國出口集裝箱班輪運輸市場11條航線的運價指數分別進行ADF檢驗發現，在或長或短的時間內，各航線運價指數均呈現隨機游走的特征，而較長期的運價指數時間序列則逐漸呈現平穩，服從均值回歸。

然而，現在還有一個疑問就是：單位根檢驗獲得的是基于最小二乘法的回歸模型，在隨機游走的模型設定中，模型（1）、（2）和（3）中均假設ut～ⅡD（0，σ2），這也就意味著單位根檢驗獲得的模型中殘差應該是獨立同分布的白噪聲，序列前后不會具有自相關和異方差等特征。

殘差項的自相關檢驗可以采用Box－Ljung Q檢驗，即要檢驗殘差項是否為獨立同分布的白噪聲。檢驗假設

式中：m為待檢驗的自相關系數的個數；n為序列中觀察值個數；Qm近似地服從χ21－α（m）分布。

當Qm＞χ21－α或PROB值（簡稱P值）小于給定顯著性水平α時，拒絕原假設H0，認為殘差序列自相關系數不為0即殘差項不是白噪聲序列；否則就接受原假設，認為殘差序列自相關系數為0，殘差項是白噪聲。

給定顯著性水平α＝0．1，現分別對前述11條航線運價指數時間序列ADF檢驗中服從隨機游走（存在單位根）的情況來檢驗模型的殘差序列是否存在自相關檢驗，用Eviews軟件運行結果總結，見表5、表6。

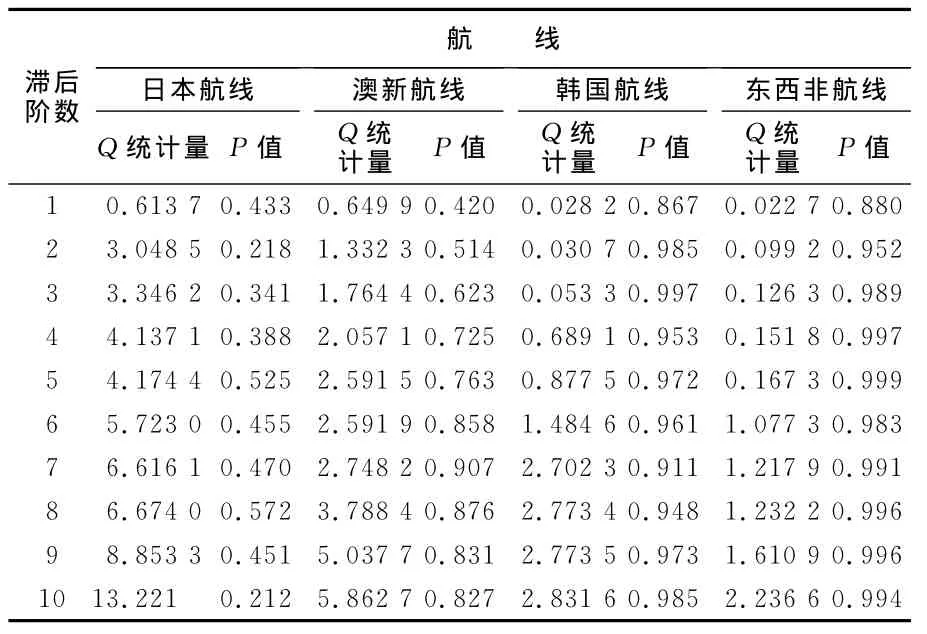
表5 第一類航線運價殘差自相關檢驗的Q統計量及其P值（2010－2011年數據）

從檢驗結果可以看出，在給定顯著性水平α＝0．1，各航線運價指數殘差自相關系數滯后1～10階的PROB值幾乎均大于給定的顯著性水平α＝0．1（僅香港航線滯后第10階P值為0．022），因此殘差基本不存在自相關性。顯然，可以判斷中國出口集裝箱班輪運輸市場運價指數在一定時期內的確具有隨機游走的特性。見表6。

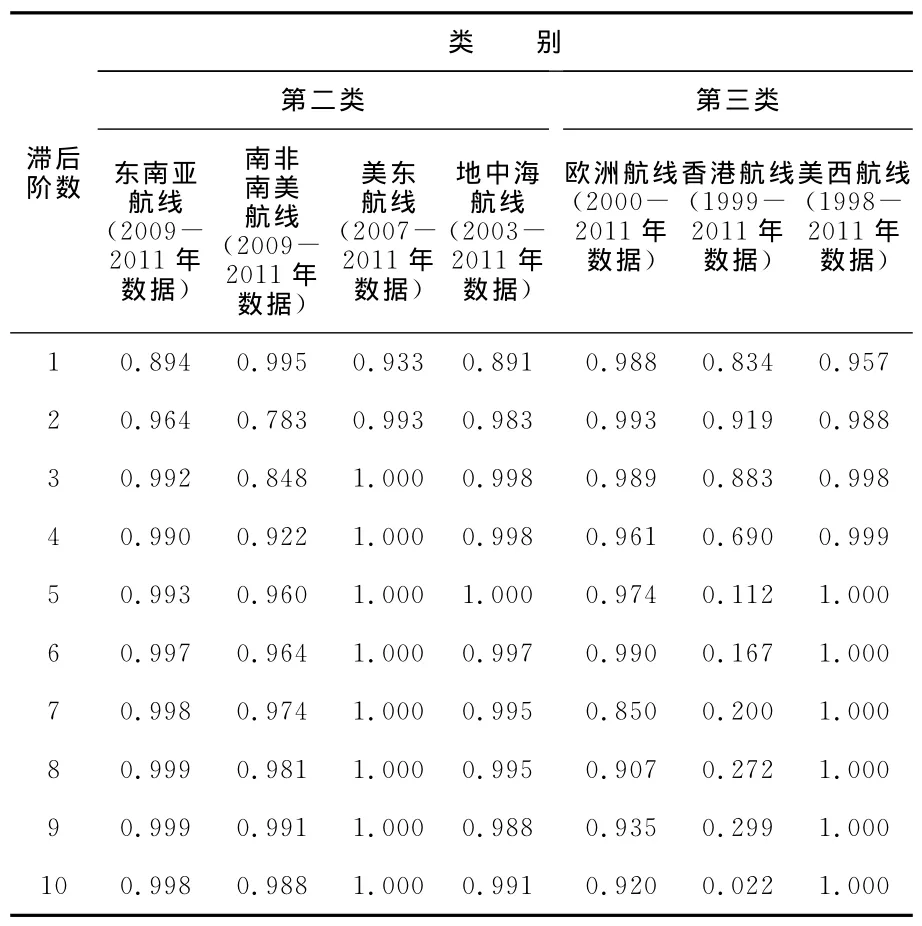
表6 第二、三類航線運價的殘差自相關性檢驗的P值

五、結 論

經過對中國國際集裝箱班輪運輸市場的11條航線運價指數進行單位根檢驗發現，在α＝0．1的顯著性水平下，運價指數在3年以內基本都是服從隨機游走的，隨著時間序列的增長，隨機游走特性逐漸減弱，14年以上的集裝箱班輪運價指數時間序列拒絕隨機游走的假設。因此，中國國際集裝箱班輪運輸市場運價指數的檢驗及分析，本文獲得以下結論：

（一）班輪運價在短期內具有隨機游走的趨勢

班輪運價受到國際國內的政治經濟等各種因素的影響，其隨機波動特性是多種因素共同作用的結果。集裝箱班輪運輸市場短期弱式有效性的表現要根據不同航線的具體情況加以區別，并不具有一般性。集裝箱班輪運輸市場運價指數的短期隨機游走特性意味著，集裝箱班輪運輸市場盡管是寡頭壟斷市場，根據美國經濟學家Fama有效市場假設理論，在短期之內市場仍然是弱式有效的。究其原因，近些年來集裝箱班輪運輸市場日趨激烈的競爭削弱了其寡頭壟斷特性，呈現出壟斷競爭的特性，使得價格能夠在短期反映出相當的市場信息。

（二）長期服從均值回歸

國際集裝箱班輪市場結構具有一定程度的壟斷競爭性，這最終導致其運價在長期具有均值回復的特性，運價反映了班輪市場的競爭結構。在相互影響、相互制約中，集裝箱班輪市場中占主導地位的若干大型班輪公司的相互競爭決定了班輪市場的供需乃至運價水平，這些往往還取決于當時的市場情況和利潤水平。其他規模較小的航運公司一般根據自身的情況采取相應的價格跟從策略。長期來看，班輪運價作為一種服務產品的價格圍繞其價值上下波動，呈現出均值回歸的特性，因此長期價格是可預測的，市場是無效的。

（三）不同航線其隨機游走時間長短不一

不同的分航線由于班輪工會或聯盟力量不一樣，對價格控制能力不一樣，表現為不同航線運價隨機游走的時間長短不一樣，對市場信息反映的能力有大小，運價指數時間序列隨機游走持續時間長的，運價反映市場信息多，價格更加不可預測，反之，運價反映市場信息能力弱，價格更容易預測。

因此，如果要進入某個班輪運輸市場，航線的選擇也至關重要，對于運價序列隨機游走持續較長的航線，由于其運價在較長時間能反映市場信息，航運企業將有更多的投資機會；相反，對于那些運價序列隨機游走時間較短的航線，市場信息較少地體現在運價變動中，班輪工會的壟斷力量越強，航運企業只有較少的投資機會。

本文的局限性在于論文中盡管滯后10階殘差自相關檢驗結果基本無自相關性，但是在給定顯著性水平α＝0．1，日本航線運價指數殘差自相關系數滯后32～33期，香港航線運價指數殘差自相關系數滯后10～14期的PROB值是小于給定的顯著性水平α＝0．1的，此時殘差存在一定的自相關性。這說明受數據序列的限制用ADF檢驗中國出口集裝箱班輪運輸市場運價指數的隨機游走有一定的局限性，筆者認為隨著時間遷移，發布的CCFI指數時間序列數據量的增加，日本及香港航線的殘差自相關性將會減弱或消失。

本文對集裝箱班輪運輸市場的運價隨機特性的研究結果，有利于各航運企業以及航運專家、學者利用班輪運價的短期隨機游走、長期均值回歸的特性對市場有效性進行正確判斷，對于準確掌握有利時機對集裝箱班輪運輸市場各航線進行運力投資、擴大經濟效益具有較大的理論意義和現實意義。

［1］Fama E F．Efficient capital market a review of theory and empirical work［J］．Journal of Finance，1970（5）：383－417．

［2］Hawdon D．Tanker freight rates in the short and long run［J］．Applied Economics，1978（3）：203－217．

［3］Berg－Andreassen J A．Some properties of international maritime statistics［J］．Maritime Policy ＆Management，1996（4）：381－395．

［4］Glen D，Rogers P．Does weight matters？A statistical analysis of the SSY capesize index［J］．Maritime Policy ＆ Management，1997（4）：351－364．

［5］Kavussanos M G．Comparison of volatility in the dry cargo ship sector LJ7［J］．Journal of Transport Economics＆Policy，1996（1）：67－92．

［6］Kavussanos M G，Alizadeh A H．Efficient pricing of ships in the dry bulk sector of the shipping industry［J］．Maritime Policy and Management，2002（3）：303－330．

［7］李序穎．中國出口集裝箱運價指數與波羅的海干散貨運價指數的實證分析［J］．數理統計與管理（S），2005，24：314－317．

［8］李耀鼎，宗蓓華．國際干散貨運價波動與隨機游走檢驗［J］．大連海事大學學報，2006（4）：5－10．

［9］陸克從．波羅的海好望角型船運價指數波動分析［J］．上海海事大學學報，2008（4）：29－33．

［10］范永輝，楊華龍，張寶華．基于灰色關聯理論的油輪運價指數波動分析［J］．大連海事大學學報，2009（4）：30－34．

［11］中華人民共和國交通部．2011年中國航運發展報告［R］．北京：人民交通出版社，2012：38－48．

［12］交通運輸部綜合規劃司．2011年公路水路交通運輸行 業 發 展 統 計 公 報 ［EB／OL］．（2012－04－25）［2012－05－10］http：∥www．moc．gov．cn／zhuzhan／tongjigongbao／fenxigongbao／hangyegongbao／201204／t20120425＿1231778．html．