LMD的LabVIEW實現及在滾動軸承故障診斷中的應用

唐貴基，王曉龍

(華北電力大學 機械工程學院，河北 保定 071003)

2005年Smith Jonathan S在EMD理論基礎上提出一種新的時頻分析方法——局部均值分解法(Load Mean Decomposition,LMD)，該方法同樣具有自適應性，可以將任何一個復雜的多分量復合信號分解成多個乘積函數(Product Function，PF)分量及一個余量相加的形式，PF分量能夠真實地反映原信號的信息[1]。相對于EMD來說，LMD受端點效應影響較小，并且可以避免EMD 算法自身存在的問題，用于故障診斷，具有一定的優勢。鑒于LMD在故障診斷領域良好的應用前景以及LabVIEW軟件在信號分析處理方面的廣泛應用，根據LMD算法理論開發出LabVIEW的LMD模塊，將更有利于測試系統的搭建。

1 LMD算法簡介

對于給定的信號x(t)，LMD算法流程為[2]：

(1)確定原信號x(t)的所有局部極值點ni。

(2)計算相鄰極點的均值和包絡估計值

(1)

(2)

(3)均值和估計值分別用直線連接后進行滑動平均處理，得到局部均值函數m11(t)和包絡估計函數a11(t)。

(4)獲得包絡信號a1(t)和純調頻信號s1n(t)。

h11(t)=x(t)-m11(t)，

(3)

s11(t)=h11(t)/a11(t)，

(4)

如果s11(t)的包絡估計函數a12(t)≠1，則將其作為原始數據重復上述過程，直到其包絡估計函數a1(n+1)(t)=1，則得到純調頻信號s1n(t)，則包絡信號為

(5)

包絡信號a1(t)即為瞬時幅值，通過純調頻信號s1n(t)即可求得瞬時頻率f1(t)為

(6)

(5)求得乘積函數分量。將包絡信號a1(t)和純調頻信號相乘即可得到第1個乘積函數分量，即

PF1(t)=a1(t)s1n(t)。

(7)

原信號x(t)減去PF1(t)后獲得新信號u1(t)，將u1(t)作為原始數據重復上述過程k次，直到余量uk(t)為單調函數或常數。

2 LMD算法的LabVIEW程序實現

LMD算法通過圖形化編程語言LabVIEW實現，經過模塊化劃分后的主程序框圖如圖1所示。

LMD主程序中包含極值延拓、樣條插值、分量判別、分量求取、余量判別、瞬時頻率求取、形態學濾波共7個子VI。其中極值延拓、分量求取和瞬時頻率求取這3個子模塊較為重要。

2.1 極值延拓子模塊

同EMD算法相比，LMD算法的端點效應程度較輕，但為了使分解過程更準確，仍需對端點進行處理。如圖2所示，該模塊采用包絡極值延拓法[3]來減少分解過程中端點效應的影響。

2.2 樣條插值子模塊

由于利用滑動平均法來平滑均值和包絡函數會產生相位差，而且平滑步長的選擇主觀性過大，分解過程存在較大誤差[4]。如圖3所示，為了減小誤差，該模塊采用三次樣條插值方法代替滑動平均法,局部均值函數可由上、下包絡線相加后求平均值得到，包絡估計函數可由上、下包絡線相減取絕對值后求平均值得到[5]。

2.3 分量判別子模塊

分量判別子模塊通過判斷當前信號是否滿足PF分量判別依據來控制循環過程，如果滿足條件，則直接輸出PF分量序列；如果未滿足條件，則持續循環，直到獲得一個PF分量。

2.4 分量求取子模塊

分量求取子模塊可通過當前獲得的包絡估計函數序列和純調頻信號序列直接計算出PF分量和瞬時幅值序列。

2.5 余量判別子模塊

為了避免分解過程進入死循環，通過余量判別子模塊對殘余分量進行控制，判斷當前信號是否分解結束，是否需要進一步繼續分解。

2.6 瞬時頻率求取子模塊

由于瞬時頻率在極值點附近存在畸變的情況，因此采用“直接法”[6]來求取PF分量的瞬時頻率，該方法簡單有效，并且不會出現沒有物理意義的負頻率，計算獲得的瞬時頻率均為正值，程序框圖如圖4所示。

圖4 瞬時頻率求取子模塊程序框圖

2.7 形態學濾波子模塊

LMD模塊對仿真信號分解后獲得的瞬時幅值和瞬時頻率曲線存在少許毛刺，形態學濾波子模塊利用形態學濾波算法[7]對其進行平滑處理。

3 軸承故障診斷實例檢驗

采用QPZZ故障診斷試驗臺模擬N205圓柱滾子軸承故障，并利用開發的LMD模塊對測得的振動數據進行分析處理，以此來驗證該模塊的可靠性及有效性。采用壓電加速度傳感器對振動信號進行數據采集，采樣頻率設置為12 800 Hz。1 440 r/min轉速時，N205軸承故障的特征頻率見表1。

表1 N205滾動軸承故障的特征頻率 Hz

3.1 滾子故障診斷

滾子發生故障時，由于滾子在自轉的同時也隨保持架一起旋轉，因此損傷點所處位置及受載呈周期性變化，系統固有頻率信號、保持架轉頻信號、滾子故障特征頻率信號互相調制生成滾動體故障信號[1]，故障信號的時域波形及頻譜如圖5所示。

從圖5可以看出，時域波形上出現明顯規律性沖擊，頻譜中出現邊頻調制的現象，由此說明軸承出現局部損傷。對故障信號進行LMD分解后得到6個PF分量，省略掉余量后各分量波形如圖6所示。

圖5 滾子故障信號的時域波形及頻譜

圖6 滾子故障信號LMD分解結果

選取經過LMD分解獲得的PF1分量的瞬時幅值曲線做進一步頻譜分析，得到的頻譜如圖7所示。從圖中發現，頻譜中有6處相對明顯的譜線，并出現調制現象，間隔頻率為保持架的旋轉頻率。104，113和133 Hz為保持架轉頻調制邊頻帶；10和20 Hz分別為保持架的轉頻及2倍頻；123 Hz為滾子故障特征頻率。結果與理論計算相吻合，由此可以說明，滾子存在局部缺陷。

圖7 滾動體故障信號PF1分量的瞬時幅值曲線的頻譜

3.2 內圈故障診斷

內圈發生故障時，由于內圈隨轉軸一起旋轉，因此內圈上的故障點與滾子的接觸位置及承受的載荷也呈周期性變化，系統固有頻率信號、軸轉頻信號、內圈故障特征頻率信號相互調制生成內圈故障信號[8]，故障信號的時域波形及頻譜如圖8所示。

圖8 內圈故障信號的時域波形及頻譜

從圖8可以看出，由于內圈存在局部缺陷并且接觸位置及受載大小的不斷變化，時域波形和頻譜上同樣出現規律性沖擊和邊頻調制的現象。在此省略內圈故障信號的LMD分解結果，只選取分解后得到的PF1分量的瞬時幅值曲線作頻譜分析，結果如圖9所示。

圖9 內圈故障信號PF1分量的瞬時幅值曲線的頻譜

從圖中發現，頻譜有6處峰值比較明顯，同樣出現調制現象，間隔頻率為軸的轉頻，124,148和196 Hz為軸轉頻調制邊頻帶；24和48 Hz分別為軸的轉頻及2倍頻;172 Hz為內圈故障特征頻率。由此可以斷定，內圈存在局部缺陷。

3.3 外圈故障診斷

外圈發生故障時，由于外圈固定，因此故障所處的位置及受載的大小保持不變，故障信號是以系統固有頻率為高頻載波，外圈特征頻率為調制頻率的調制信號[7]，信號的時域波形及頻譜如圖10所示。

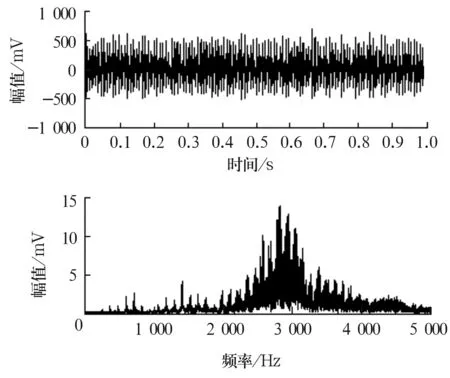
圖10 外圈故障信號的時域波形及頻譜

與前兩種故障不同，由于外圈損傷點所處位置及受載大小基本不變，因此時域波形上的振動沖擊的振幅比較均勻，外圈故障信號LMD分解獲得的PF1分量的瞬時幅值曲線的頻譜如圖11所示。

圖11 外圈故障信號PF1分量的瞬時幅值曲線的頻譜

從圖中發現，頻譜在116和233 Hz處存在明顯的峰值，分別對應著軸承外圈故障特征頻率及2倍頻，分析結果與理論計算相符，因此判定，外圈存在局部故障。

4 結束語

同EMD算法一樣，LMD算法也是一種適合處理非線性非平穩信號的時頻分析方法，該方法可以有效地應用于齒輪、軸承或轉子系統的故障診斷。在LabVIEW平臺上將LMD算法程序化，并通過對實測軸承故障信號的分析，證明基于LabVIEW平臺開發的LMD模塊能夠準確地對故障信號進行分析，順利提取出軸承的故障特征頻率信息。