高鐵軸承試驗臺粉塵箱中氣固兩相流動的數值模擬

王菲，劉永剛，宋黎明，楊文卓

(1. 河南科技大學 機電工程學院，河南 洛陽 471003；2.河南省機械設計及傳動系統重點實驗室，河南 洛陽 471003)

高速鐵路從20世紀60年代進入使用階段以來，運行速度不斷提高，其中以日本、法國和德國等的高速鐵路發展最為突出。隨著高速鐵路的飛速發展，也帶動了高速鐵路軸承技術的發展與進步，高速鐵路軸承的主要供貨商，如：SKF，FAG及NTN都擁有先進的軸承試驗技術和試驗裝置，其中SKF與FAG所用的高速鐵路軸承試驗機，軸承的試驗速度已經達到550 km/h，同時可以模擬軸承運行環境，如風速和溫度等對軸承性能的影響。由于我國高速鐵路的發展起步較晚，現有的鐵路軸承試驗技術與國外還存在著一定的差距。中國現已成為世界高鐵大國，包括軸承在內的許多關鍵技術，必須盡快掌握和擁有自主知識產權，才能真正具備高端市場的核心競爭力[1]。因此，需要加強300 km/h高速鐵路軸承試驗臺的開發，為高速鐵路軸承的設計制造提供試驗數據支撐，以滿足我國高速鐵路的發展要求。

防粉塵性能試驗臺是對高速鐵路軸承進行試驗和測試的重要設備，該試驗臺能夠模擬軸承的實際工況并進行防粉塵密封性能試驗。模擬溫度范圍為室溫至100 ℃，一次可試驗2套(或2對)鐵路軸承。其中粉塵箱是模擬軸承工況和進行試驗的關鍵部件。對粉塵箱內部的氣固兩相流場進行仿真分析不僅能對粉塵箱的設計提供一定的指導，更有利于降低試驗成本。但由于受軸承試驗臺粉塵箱內部顆粒的旋轉、黏性和粉塵箱壁面的影響，其內部流場非常復雜，流場中同時存在著湍流、層流以及可能出現的分離流、尾流和射流等流動現象，而粉塵箱內輸送的流體屬于氣固兩相混合物，故應考慮氣固兩相間的相互作用，研究難度較大。

下文采用CFD方法對粉塵箱內氣固兩相流動進行數值模擬，利用Fluent提供的湍流模型和離散相模型對粉塵箱內氣流場中的固體顆粒的運動進行仿真，從而定性分析不同直徑顆粒在粉塵箱內的運動軌跡。

1 氣固兩相流的計算模型

目前用于描述氣固兩相流場變化的數理模型主要有基于Euler坐標系的連續介質模型、基于Euler-Lagrange坐標系的顆粒軌道模型和顆粒流體模型[2]3類。顆粒軌道模型可在充分考慮顆粒與流體間相互作用的前提下，模擬出復雜歷程的顆粒相軌跡，同時節省計算存儲量[3]。故選擇顆粒軌道模型即Euler-Lagrange方法[4-5]對應的Fluent離散相模型進行分析。在Euler-Lagrange方法中，將流體相視為連續相，并且求解N-S方程，而離散相可通過計算流場中大量粒子的運動而得到。

Fluent軟件通過積分拉氏坐標系下的顆粒作用力微分方程來求解離散相顆粒(液滴或氣泡)的軌跡[6]。顆粒作用力平衡方程(顆粒慣性力=作用在顆粒上的各種力)在笛卡爾(Cartesian)坐標系下的形式(x方向)為

(1)

(2)

式中:FD為顆粒的單位質量曳力；Fx為顆粒的附加質量力；u為流體相速度；up為顆粒速度；μ為流體動力黏度；g為重力加速度；ρg為流體密度；ρp為顆粒密度；dp為顆粒直徑。

相對Reynolds數(顆粒Reynolds數)為

(3)

拖拽系數為

(4)

式中：系數a1,a2,a3按照Morsi和Alexander提出的方法確定。

顆粒所受的作用力有以下幾種。

(1)重力。由于研究的是稀相流動，所以可忽略顆粒重力的影響。

(2)其他作用力。(1)式中包含的其他作用力Fx在某些情況下可能很重要，其中最重要的一項是所謂的“視質量力”(附加質量力)，它是由于要使顆粒周圍流體加速而引起的附加作用力。視質量力為

(5)

當ρg>ρp時，視質量力不可忽視。流場中存在的流體壓力梯度引起的附加作用力為

(6)

(3)Saffman升力。在附加力中也可以考慮由于橫向梯度(剪切層流動)導致的Saffman升力，

(7)

式中：K=2.594；dij,dlk，dkl為流體變形速率張量。該式僅適用于較小顆粒的Reynolds數流動。

顆粒軌跡模型以及描述顆粒質量/熱量傳遞的附加方程都是在離散的時間步長上逐步進行積分運算求解的。對(1)式積分就可得到顆粒軌跡每個位置上的顆粒速度。顆粒軌跡為

(8)

沿著每個坐標方向求解此方程就得到了離散相的軌跡。

2 數值分析

試驗臺粉塵箱結構復雜，主要部件由被試軸承、密封圈、軸承座、陪試軸承、推桿和頂桿等組成。其中被試軸承、密封圈、陪試軸承等徑向尺寸變化不大，約為350 mm左右，在建立幾何模型時簡化為直徑350 mm的圓柱體。而推桿、頂桿等的作用是對被試軸承施加軸向及徑向載荷，直徑30 mm的圓桿對顆粒流場分布影響不大，故可在模型中忽略。為對試驗臺粉塵箱內部工況進行氣固兩相流的數值模擬，作如下假設：(1)流體在流動過程中不可壓縮；(2)忽略固體粒子間的相互作用；(3)固體粒子占體積的比例小于10%，粒子的存在對氣流參數的影響很小；(4)假定固體粒子是直徑相同、密度均勻的球體；(5)氣固兩相流具有相同的溫度場；(6)粉塵顆粒在氣流中受到的力主要是氣體的黏滯阻力，其他力可以忽略不計；(7)不考慮固相與壁面的摩擦力。

試驗臺密封箱主要用于給被試高鐵軸承提供符合實際工況的環境。要求箱內溫度達100°左右，粉塵顆粒應盡可能均布于被試軸承周圍。首先，設定進口邊界條件，給出試驗臺粉塵箱進口處氣相流和固相的速度：設進口氣相流速度u為10,100 m/s；湍流動能強度為10%。水力直徑(根據進口尺寸給定)為145 mm；設固體和氣相流的容積率為10%，顆粒直徑大小依次取10，50，100，200和300 μm，材料屬性為二氧化硅。

然后，設定出口邊界條件。試驗臺粉塵箱由左、右兩部分組成，用螺栓固定，連接部分存在一定的泄漏，故在建模時設置上、下兩個泄漏口。在粉塵箱右側出口處，由于初始邊界上的壓力或速度均未知，所以出口的絕對壓力為0，設定為自由流出。

試驗臺粉塵箱徑向示意圖如圖1所示。利用前處理軟件Gambit建立試驗臺粉塵箱的幾何模型，并用四邊形網格進行網格劃分(圖2)，在模型中心區域由于流動梯度變化比較快，故網格較密，而梯度變化較緩慢的區域網格稀疏，以減小計算量。網格劃分完后指定邊界條件，然后將模型導入Fluent進行模擬計算。

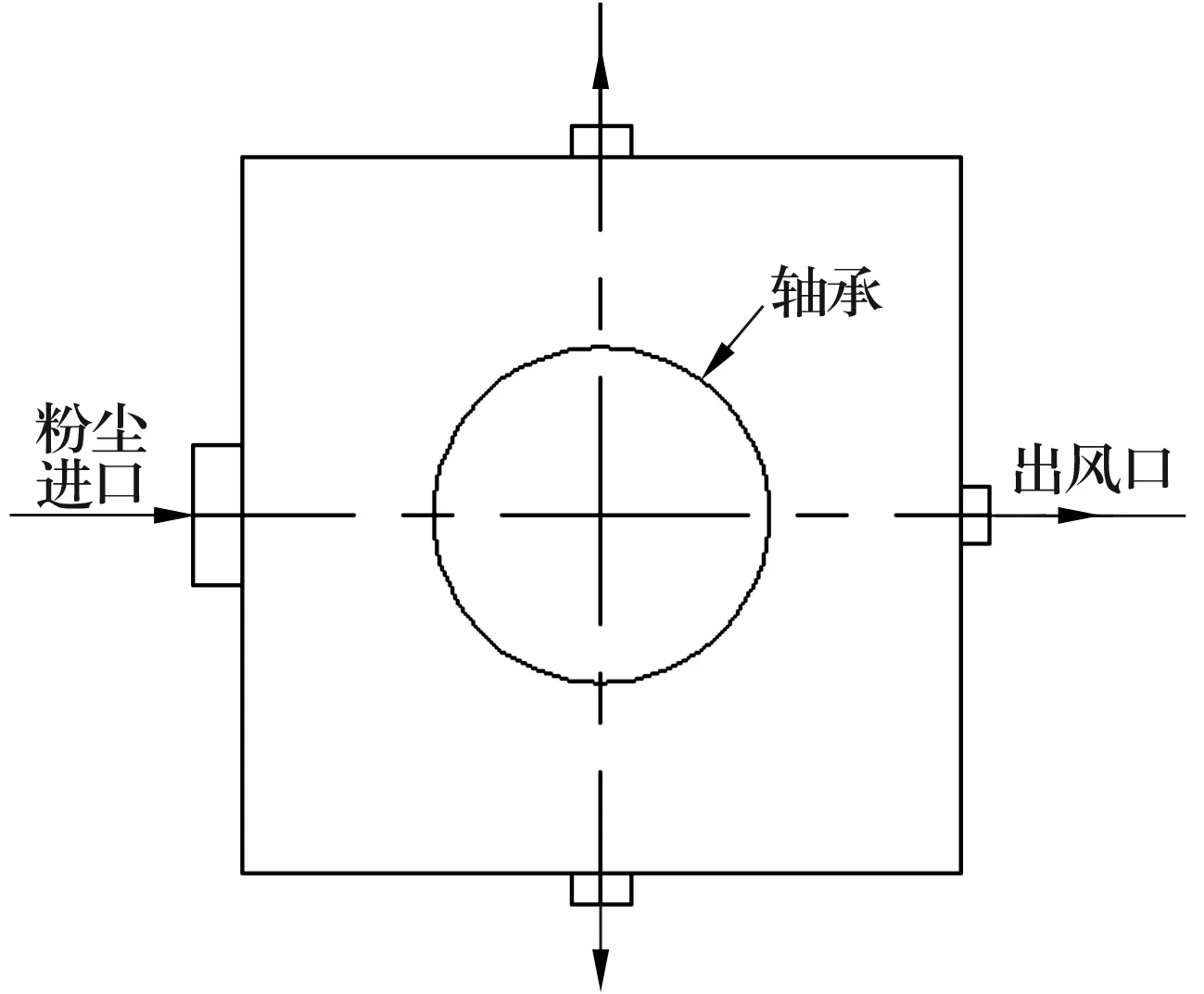
圖1 試驗臺粉塵箱徑向示意圖

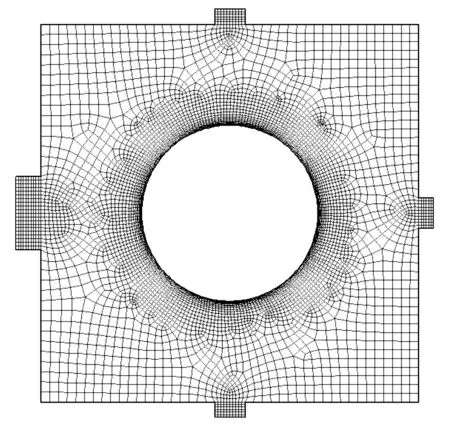
圖2 網格圖

3 結果分析

圖3所示為進口速度為10 m/s時的氣流速度場分布云圖。低速分布區大致為箱體前半部分上、下兩角形成的渦流區域，軸承迎風壁面附近-10°～10°區域。經軸承迎風面后發生了繞流現象，在背風面形成了低速回流區。高速分布區域為軸承迎風壁面附近10°～80°，-80°～-10°區域和粉塵箱右邊的出口區域。

為了研究粉塵顆粒在箱體里的分布，其他邊界條件不變，設粉塵粒徑dp分別為10，50，100，200和300 μm，分別得到粉塵在箱體中的分布規律，如圖4～圖8所示。

圖4 dp=10 μm時粉塵顆粒的運動軌跡

圖5 dp=50 μm時粉塵顆粒的運動軌跡

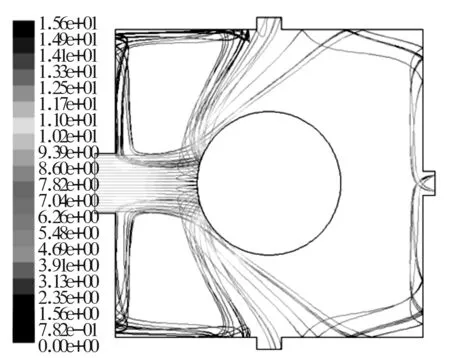
圖6 dp=100 μm時粉塵顆粒的運動軌跡

圖7 dp=200 μm時粉塵顆粒的運動軌跡

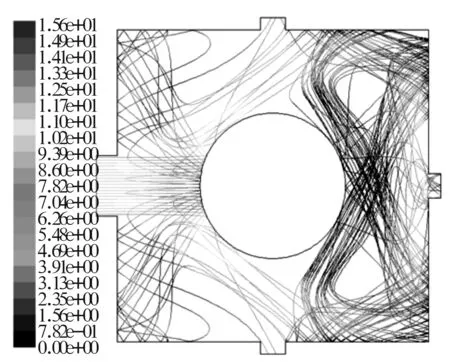
圖8 dp=300 μm時粉塵顆粒的運動軌跡

固體顆粒尺寸無論大小，在整個運動過程中運動軌跡都會向箱壁靠近，但靠近的速度和位置有所不同。當粒徑dp=10 μm時，由于慣性作用較小，其軌跡較短且更接近流線，在出氣管段幾乎完全隨氣流運動。小顆粒粉塵向箱壁靠近的速度較慢，一般集中在箱的右半區域，僅有部分顆粒與箱壁相撞。隨著粒徑的增大，顆粒向箱壁靠近的速度加快，與箱壁相撞的位置朝進口方向移動，在箱體左半區有部分顆粒與壁面相撞。當粒徑dp=300 μm時，其運動軌跡較長，大都與軸承壁面相撞后與箱壁發生反復碰撞。

在箱體左半區，塵粒以較高的速度撞向軸承表面，大直徑的塵粒每碰撞一次后，其速度就會降低。而小直徑顆粒碰撞一次后，很快就因氣流的作用使其速度變得與氣流相當，顆粒的跟隨性較好。在箱體右半區，顆粒受到低速回流區的影響，較小的顆粒會隨氣流流出，而尺寸較大的顆粒會有部分產生沉降。但無論顆粒大小，顆粒在離開粉塵箱的瞬間，其速度均達到最大。

當進口速度為100 m/s時，箱體內氣流速度場如圖9所示。可以看出，當進口速度增大時，在軸承的背風面形成的低速回流區域變大。圖10為進口速度為100 m/s，dp= 10 μm時粉塵的運動軌跡。與圖4相比，粉塵朝箱壁靠近的位置向后發生了偏移，又由于受到箱體右半部分低速回流區域的影響，顆粒運動軌跡較進口速度為10 m/s時更接近箱壁。對于直徑為50，100，200和300 μm的粉塵顆粒，當進口速度為100 m/s時，顆粒的運動軌跡也發生了明顯改變。綜上所述，當進口速度改變時，粉塵顆粒在箱體內的運動軌跡也發生相應的變化。

圖9 進口速度100 m/s時箱體中氣流速度場分布云圖

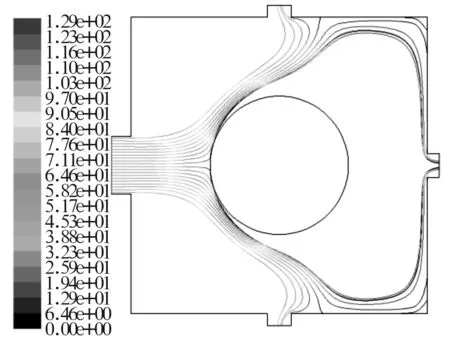
圖10 進口速度100 m/s,dp=10 μm時粉塵的運動軌跡

4 結論

(1)小顆粒跟隨性較好，隨著顆粒直徑的增大，與箱體相撞的位置向左側移動，大顆粒大都與箱體左壁相撞;

(2)隨著顆粒直徑的增大，軌跡線變長，顆粒在箱體內的碰撞次數增多，其運動到箱壁右出口處速度達到最大；

(3)大顆粒在軸承背風面的低速回流區會有一定的沉降；而小顆粒隨氣流流動趨勢明顯，大都隨氣流離開粉塵箱。