圓心角90°的扇形的圖形特征例析
☉安徽省廬江第五中學 許和平
圓心角90°的扇形的特征由它的圖形構成所決定,一是有四分之一的圓弧,具有圓中的有關基本性質;二是有一個90°的圓心角,具有直角三角形、矩形等圖形的幾何性質,再通過圓弧上的動點設計,結合未知數,滲透數形結合思想,可命制一些具有特色的新型綜合性試題.下面以中考壓軸題和競賽題為例加以分析研究.
例1(2000年上海市中考試題)如圖1,在半徑為6、圓心角為90°的扇形OAB的弧AB上有一個動 點P,PH⊥OA, 垂 足 為H,△OPH的重心為G.

圖1
(1)當點P在弧AB上運動時,在線段GO、GP、GH中,有無長度保持不變的線段?如果有,請指出這樣的線段,并求出相應的長度;
(2)設PH=x,GP=y,求y關于x的函數解析式,并寫出函數的定義域;
(3)如果△PGH是等腰三角形,試求出線段PH的長.
解:(1)在線段G0、GP、GH中,有長度保持不變的線段,這條線段是GH.延長HG交OP于點E,延長PG交OH于點D.

(2)在Rt△OPH中,

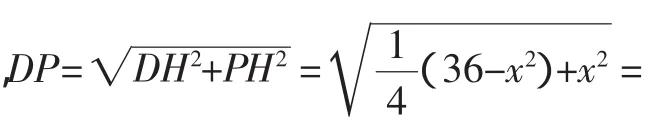
(3)△PGH是等腰三角形有三種可能情況:
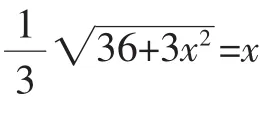

③PH=GH,即x=2.
綜上所述,如果△PGH是等腰三角形,那么線段PH的長等于或2.
評析:第(1)小題中主要抓住了同圓的半徑相等的性質,雖然點P在弧AB上運動,但OP是⊙O的半徑始終保持不變,即OP=6.再結合直角三角形和三角形重心的性質,使所求線段GH與已知半徑OP聯系起來,從而使問題解決.在第(3)小題中,已知△PGH是等腰三角形,但題中沒有指明哪兩邊是腰,因此解題中必須對三角形的三邊進行分類討論解決,滲透了數學中的分類思想.
例2(2008年廣州市中考試題)如圖2,扇形OAB的半徑OA=3,圓心角∠AOB=90°,點C是弧AB上異于A、B的動點,過點C作CD⊥OA于點D,作CE⊥OB于點E,連接DE,點G、H在線段DE上,且DG=GH=HE.
(1)求證四邊形OGCH是平行四邊形.
(2)當點C在弧AB上運動時,在CD、CG、DG中,是否存在長度不變的線段?若存在,請求出該線段的長度.
(3)求證CD2+3CH2是定值.
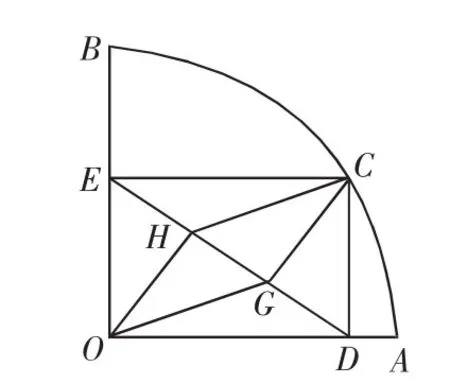
圖2
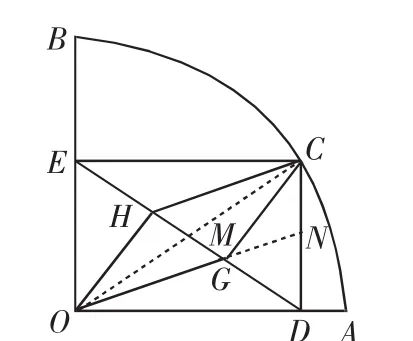
圖3
解:(1)如圖3,連接OC交DE于M,由矩形得OM=CG,EM=DM.
因為DG=HE,所以EM-EH=DM-DG,得HM=DG.
所以四邊形OGCH是平行四邊形.
(2)DG不變,在矩形ODCE中,DE=OC=OA=3,
(3)方法一:利用三角形的中位線與勾股定理.

評析:本解法充分利用了題中的三等分點、平行四邊形和三角形中位線的性質,較好地實現了把線段ON轉化為線段CH的倍分關系,再以Rt△OND為基礎,通過勾股定理,使問題得以解決.
方法二:利用相似三角形與勾股定理.
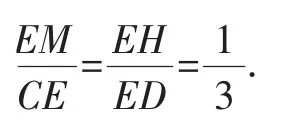
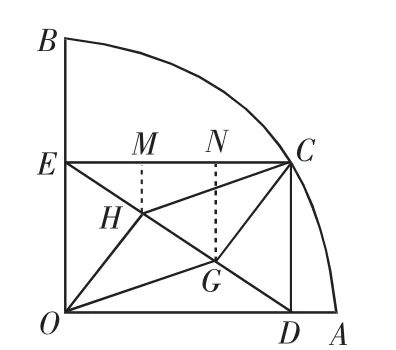
圖4
因為CE=,所以EM=
在Rt△CMH中,因為CH2=CM2+MH2,
評析:本解法充分利用了題中的三等分點、相似三角形的性質,得出相關線段關于x的代數式,再以Rt△CMH為基礎,通過勾股定理,使問題得以解決.
方法三:利用三角形面積與勾股定理.
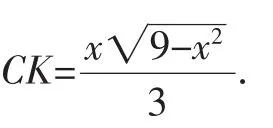
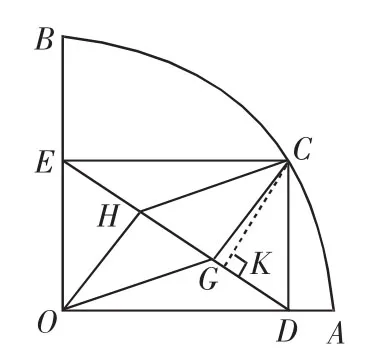
圖5
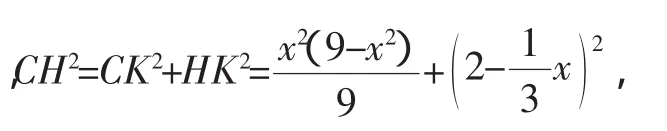
評析:本解法充分利用了幾何中的面積法,得出斜邊上的高CK和HK關于x的表達式,再以Rt△CKH為基礎,通過勾股定理,使問題得以解決.
方法四:三角函數與勾股定理.
如圖5,過點C作CK⊥ED于K,在Rt△CEK和Rt△CHK中,由勾股定理得:
CE2-EK2=CH2-HK2,
故CH2=EC2+(HK2-EK2)=EC2+(HK+EK)(HK-EK)=EC2+EH(HK+EK)=EC2-EH(2EK-EH)=EC2+EH2-2EH×EK.
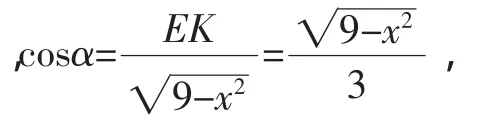
評析:本試題較好地發揮了圓心角為90°的扇形的圖形特征,所涉及的知識點有:同圓的半徑相等,矩形的判定和性質,平行四邊形的判定,勾股定理,相似三角形或三角函數等.第(1)小題比較基礎,學生容易解決,第(2)小題只利用矩形的性質求解,涉及到課標不要求的三角形重心的性質求解,三個小題有一定的梯度,層次分明,特別是第(3)小題有一定的難度,但解題入口較寬,可以從不同的角度進行分析,得出不同的解題思路,注重考查學生運用已學知識分析問題和解決問題的能力.
例3(2012年上海市中考試題)如圖6,在半徑為2的扇形AOB中,∠AOB=90°,點C是弧AB上的一個動點(不與A、B重合),OD⊥BC,OE⊥AC,垂足分別為D、E.
(1)當BC=1時,求線段OD的長.
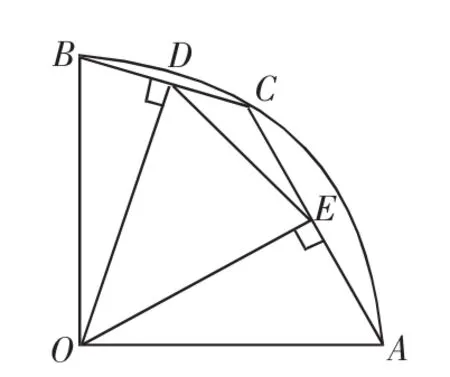
圖6
(2)在△DOE中是否存在長度保持不變的邊?如果存在,請指出并求其長度;如果不存在,請說明理由.
(3)設BD=x,△DOE的面積為y,求y關于x的函數關系式,并寫出自變量的定義域.
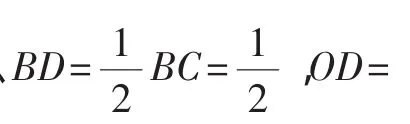
(2)存在,DE是不變的,如圖7,連接AB且AB=2
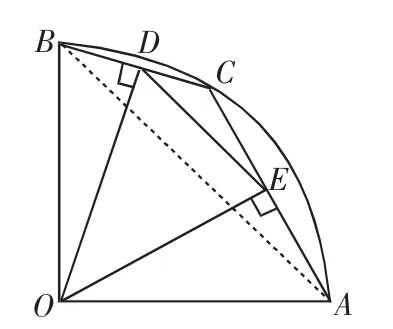
圖7

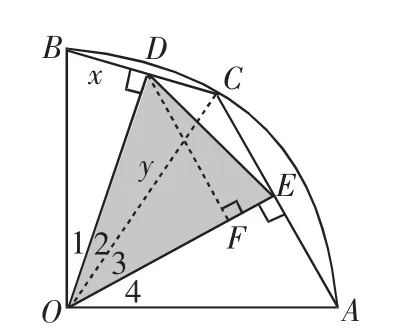
圖8
(3)如圖8,將x移到要求的三角形中去,所以
由于∠1=∠2,∠3=∠4,所以∠2+∠3=45°.
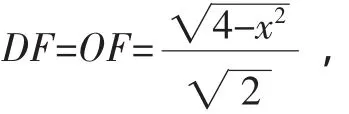
評析:本題起點低,第(1)小題先把運動中的點C固定,BC是一個定值,BC是圓弧中的弦,利用垂徑定理和勾股定理易得OD的長度,同時也為第(2)、(3)小題的解決起到引領作用.第(2)小題隨著點C在弧上運動,但利用垂徑定理在運動的過程中,弦BC、AC的長度在發生變化,但D、E是弦BC、AC的中點的位置始終保持不變,所以DE線段是兩中點的連線,容易想到三角形的中位線.第(3)小題較好地利用了90°角的作用,通過垂徑定理和等腰三角形三線合一的性質,得出了一個特殊角45°,構造出一個等腰直角三角形,使變量x、y通過三角形的面積建立了關系.本題是一道幾何、代數的綜合題,命題者較好地發揮了90°角扇形圖形中蘊含的幾何性質,通過設置動點和未知數使問題更具有探索性和綜合性,更有利于考查學生的思維過程和分析能力.
例4(2012年全國初中數學競賽預賽)如圖9,扇形OMN的半徑為1,圓心角是90°.點B是弧MN上一動點,BA⊥OM于點A,BC⊥ON于點C,點D、E、F、G分別是線段OA、AB、BC、CO的中點,GF與CE相交于點P,DE與AG相交于點Q.

圖9
(1)求證:四邊形EPGQ是平行四邊形;
(2)探索當OA的長為何值時,四邊形EPGQ是矩形;
(3)連接PQ,求3PQ2+OA2的值.
解:(1)如圖10,因為∠AOC=90°,BA⊥OM,BC⊥ON,所以四邊形OABC是矩形.
所以AB∥OC,AB=OC.
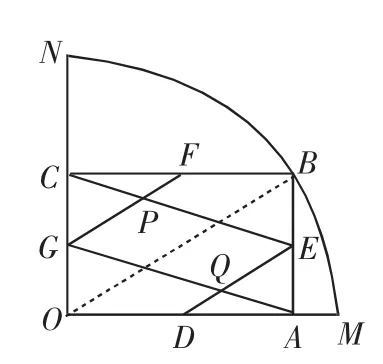
圖10
又E、G分別是AB、CO的中點,所以AE∥GC,AE=GC.所以四邊形AECG為平行四邊形.所以CE∥AG.
連接OB,因為點D、E、F、G分別是線段OA、AB、BC、CO的中點,所以GF∥OB,DE∥OB,所以PG∥EQ,所以四邊形EPGQ是平行四邊形.
(2)如圖11,當∠CED=90°時,四邊形EPGQ是矩形,此時∠AED+∠CEB=90°.
又∠DAE=∠EBC=90°,
所以∠AED=∠BCE.
所以△AED∽△BCE.

圖11
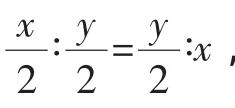


(3)如圖12,連接GE交PQ于O′,則O′P=O′Q,O′G=O′E.過點P作OC的平行線分別交BC、GE于點B′、A′.
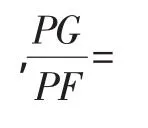

圖12
在Rt△PA′O′中,PO′2=PA′2+A′O′2,
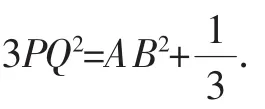

以上四例都是從圓心角90°的扇形的圖形特征入手,巧妙地運用多種方法解決不同的問題,希望通過上述解題分析,能使學生對這類題型的解答有更深刻的領悟和理解.

