分類討論思想在解題教學中的實踐和思考

☉江蘇省南通市通州區育才中學 黃新顏

數學思想方法是中學數學教學的最高境界，用華羅庚大師的話說：教師首先教學生的是數學的雙基知識，這只不過是數學的分散知識點，好像一維的數軸；其次教師應該指導學生進行知識點之間的聯系，也就是現在中考常常出現的知識點交匯處的考查，好像是二維的坐標系一般；最后教師應帶領學生走進數學思想方法的殿堂，這里才是數學最漂亮、最完美的地方，猶如是一個變換般的三維空間.因此，中學數學教學的核心是數學思想方法的教學.

眾所周知，分類討論思想是初中數學的重要思想方法，在解決很多初中數學問題時有著不可替代的作用.其早在中國古代劉徽等人的專著《九章算術》中就已經被多次使用，如今更是在中考數學中層出不窮，成為區分學生思想完整性、發散性、靈活性、嚴謹性等的必備數學思想，值得教師研究和深化.

一、在函數問題中的運用

例1 （蘇州2012年中考模擬）如圖1，已知A、B是線段MN上的兩點，MN=4，MA=1，MB＞1. 以A為中心順時針旋轉點M，以B為中心逆時針旋轉點N，使M、N兩點重合成一點C，構成△ABC，設AB=x.

（1）求x的取值范圍；

（2）若△ABC為直角三角形，求x的值；

（3）探究△ABC的最大面積.

分析：點B在AN上運動，通過觀察可得∠CAB和∠ACB可以成為直角，∠CBA不可能成為直角.

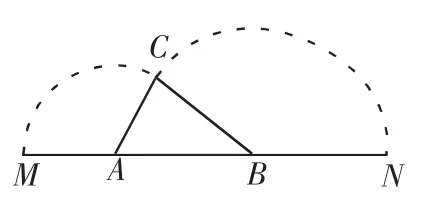
圖1

（1）根據三角形的基本性質：兩邊之和大于第三邊以及兩邊之差小于第三邊，找尋關于x的不等式，進而得出x的取值范圍；

（2）對Rt△ABC進行分析，由勾股定理進行分類，討論存在性；

（3）把△ABC的面積S的問題，轉化為S2的問題，AB邊上的高CD要根據位置關系分類討論，分CD在三角形內部和外部兩種情況.

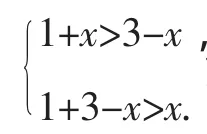
（2）①若AC為斜邊，則1=x2+（3-x）2，即x2-3x+4=0，此方程無實根；

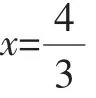
①如圖2，若點D在線段AB上，則=x，得平方得 （3－x）2－h2=x2－2x，得，平方得x（21－h2）=9x2－24x+16.整理，得x2h2=－8x2+24x－16，所以

②如圖3，若點D在線段MA上，則

圖2

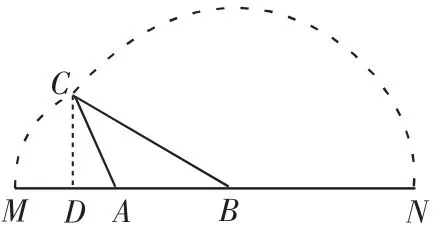
圖3

二、在應用題型中的運用

例2（2011年南京中考）學生甲和乙分別站在一邊長為10的正方形ABCD的點A和點D處，現在甲從點A出發，設其在正方形邊界上沿著逆時針勻速運動（如圖4），速度為每秒2個單位（位置記為點P），求學生甲（點P）和學生乙（點D）之間的距離.

分析：學生甲從點A出發，到達B、C、D、A的時間分別是5秒、10秒、15秒、20秒，顯然對問題的分析要以時間的臨界狀態為分類討論的切入點，因此：

圖4

（1）當0≤t＜5時，學生甲的位置P落在線段AB上，此時

（2）當5≤t＜10時，位置P在線段BC上，此時PD=

（3）當10≤t＜15時，學生甲的位置P落在線段CD上，此時

（4）當15≤t≤20時，學生甲的位置P落在線段DA上，此時

綜上可知：學生甲（點P）和學生乙（點D）之間的距離可用一個分段函數表示，下略.

提示：本題在實際應用型問題的背景下，體現了問題的運動觀點 （也是函數思想在實際應用型問題中的體現），考查了學生甲（點P）和學生乙（點D）之間的距離，應根據點P的不同位置分析不同情形，而分類討論的關鍵切入點在于正方形每個轉折處.

三、在方程中的運用

例3 求使關于x的方程kx2+（k+1）x+（k－1）=0的根都是整數的所有k值.

分析：本題中并未說明方程一定是二次方程，所以首先要對k是否等于0進行分類.當k=0時，顯然所給方程為一次方程，有整數根x=1；當k≠0時，可以設兩個整數根為x1、x2，由韋達定理可知：

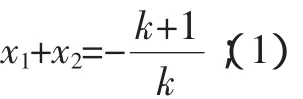
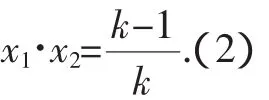
（1）－（2）得：x1+x2－x1x2=－2，有：（x1－1）（x2－1）=3=1·3，因此：

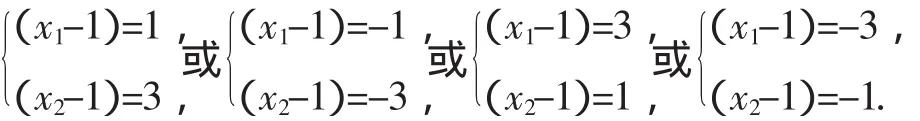
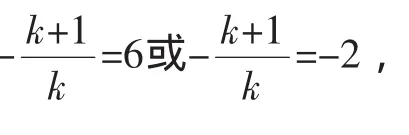
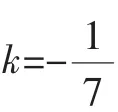
提示：對于方程問題，首先不要將思維定勢在二次方程中，教師只有引導學生抓住了分類討論的動因，把握住了分類的標準，才能做到分類時條理清楚、標準一致，在解答問題時就不會重復或遺漏，才能保證解題的準確率.

四、數學思想教學的思考

初中數學有很多的基本知識，我們稱之為雙基知識，這是學生必須掌握的一維知識點；其次初中數學知識點板塊之間的綜合運用，稱之為知識交匯處，需要教師通過一定指導，使學生通過訓練達到，即所謂學生的二維知識鏈；初中數學學習的最高境界是掌握數學思想方法，即所謂的三維知識模塊，將千變萬化的試題化有形于無形中，通過思想方法看到問題的本質、解決的思路，這是每個優秀學生學習的最終目標.熟練掌握初中數學思想方法對每個學生來說并不容易，因為這首先需要一維知識點和二維知識鏈的熟練掌握，其次才是運用這些思想——為了將我們遇到的問題進行解決或轉化.眾所周知，學生學習數學思想方法有一個循序漸進的過程，首先應學會數學的雙基知識，其次對知識進行整合獲得知識間的聯系，最終才是用數學思想方法進行提煉，將其牢固的粘合于學生的知識體系中.通過上述案例，筆者認識到分類討論思想在教學中的重要性，更能從分類討論思想中管窺中學數學教學中思想方法教學的重要性.

（1）掌握數學思想方法是學習數學知識的本質，數學思想方法滲透于數學的各個分支，是我們解決數學問題的重要導向，是探究性學習的重要工具之一.把掌握數學方法和思想作為數學教育的重點，可以使初中學生逐步掌握數學基本方法和數學思維，進而展開高效率的數學學習.數學方法和思想是初中學生提高數學素養、培養創新能力的關鍵，是一切數學創新的源泉，數學思想方法的教育使數學教學真正變為“授之以漁而非授之以魚”，讓初中學生由“學會”變成“會學”，為其今后終生學習奠定基礎.

（2）數學思想方法的教學使學生更容易理解數學科的內容，使其在掌握了一些數學思想方法后再去看待相關的數學知識顯得“高屋建瓴”.挖掘初中更深層次的問題，這樣的學習更具穩定性，有利于舊知識的鞏固和新知識的學習，能夠順利將新知納入到自身知識體系中去，數學思想方法正是體現了這么一種核心.

近年來，對初中數學思想方法的考查越來越受到各地中考的重視，教師在教學中也要從初一的教學開始就全面滲透對數學思想方法的學習，提升學生通過問題看本質的能力，使其在掌握扎實的雙基的同時，將知識點進行有機的整合，最終上升到思想方法的高度進行提煉，久而久之，就可以提升優秀學生的數學能力和數學素養，用諾貝爾獎獲得者李政道教授的話說：“我覺得今天取得的一點成就離不開數學的功底，而數學的功底又在于我當年中學時代對數學思想方法的理解和運用，其伴隨我研究一生.”

總之，數學思想方法是研究數學中發現、發明、創新和其他創造性思維活動的規律和方法，以及探索數學發展的一門科學.數學已經滲透到各個領域，并成為其思想和行動的指南，數學思想方法是一種思維，一種思考問題的方法模式，它體現了辯證法的原理，它不僅用于解決數學問題，更可以應用在人們日常的事務處理、問題思考中.

1.徐利治.數學方法論選講［M］.武漢：華中理工大學出版社，2000.

2.波利亞.數學與猜想［M］.北京：科學出版社，1984.

3.臧雷.“數學思想方法研究綜述”［J］.中學數學教學參考，2002（10）.

4.劉曉玫.論數學思想方法在數學教育中的作用［J］.首都師范大學學報，2001（10）.