借“畫板”之手，破中考?jí)狠S——對(duì)一道中考填空壓軸題的思考

☉廣東省佛山市順德區(qū)龍江龍山初級(jí)中學(xué) 鄧?yán)^雄

以函數(shù)圖像為背景，根據(jù)函數(shù)圖像的性質(zhì)，結(jié)合幾何圖形的基本性質(zhì)進(jìn)行相關(guān)的計(jì)算或證明，是中考數(shù)學(xué)的熱門題目.現(xiàn)提供一道中考填空壓軸題，并提出個(gè)人的見(jiàn)解，與同行交流探討，以期在今后的解題教學(xué)中有所幫助.

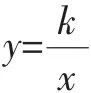
（1）當(dāng)點(diǎn)O′與點(diǎn)A重合時(shí)，點(diǎn)P的坐標(biāo)是______；

（2）設(shè)P（t，0），當(dāng)O′B′與雙曲線有交點(diǎn)時(shí)，t的取值范圍是________.

圖1

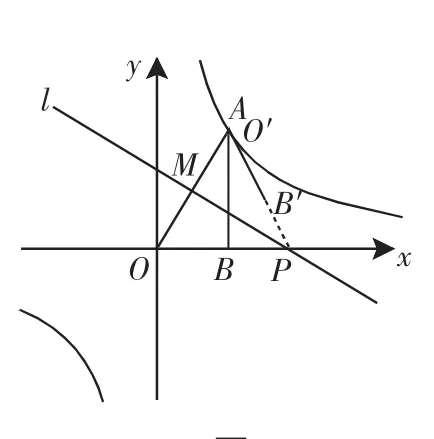
圖2

分析：由題意可知，直線l為題中軸對(duì)稱變換過(guò)程中的對(duì)稱軸，且PM⊥直線OA.

由∠AOB=60°，知：

∠OPM=30°.

由軸對(duì)稱變換可知：

∠O′PM=∠OPM=30°.

所以∠OPO′=60°.

所以△OPO′是等邊三角形（如圖2）.

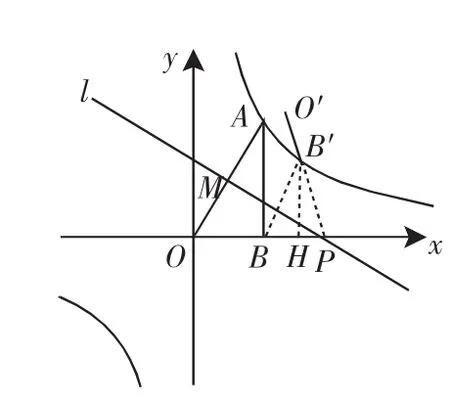
圖3

如果連接BB′，則有△BPB′也是等邊三角形（如圖3）.

根據(jù)以上關(guān)系，我們就可以解決該填空題了.

解答：（1）當(dāng)點(diǎn)O′與點(diǎn)A重合時(shí)，如圖2，

因?yàn)锽點(diǎn)的坐標(biāo)是（2，0），即OB=2，而∠AOB=60°，所以O(shè)A=2OB=4.

因?yàn)椤鱋AP是等邊三角形（具體過(guò)程不再重復(fù)），

所以O(shè)P=OA=4，即點(diǎn)P的坐標(biāo)是（4，0）.

說(shuō)明：第（1）題因?yàn)槲恢帽容^特殊，點(diǎn)O′與點(diǎn)A重合，圖形非常直觀，關(guān)系比較明顯，答案容易求出，屬于常規(guī)題.

（2）容易求得點(diǎn)A的坐標(biāo)是（2，2），而雙曲線經(jīng)過(guò)點(diǎn)A，可以求出反比例函數(shù)的解析式為①；由圖2中△OPO′是等邊三角形可知，O′、B′所在的直線經(jīng)過(guò)點(diǎn)P，且與x軸所成的角等于60°，于是設(shè)直線O′B′的解析式是y=－x+b，把點(diǎn)P的坐標(biāo)（t，0）代入求出直線O′B′的解析式是y=－x+t②.如果僅考慮直線O′B′與雙曲線有交點(diǎn)，則由①、②組成方程組，整理得x2－tx+4=0，方程有解必須滿足Δ≥0，即t2－16≥0，解得t≥4或t≤－4.

考慮本題是線段O′B′與雙曲線有交點(diǎn)的相關(guān)問(wèn)題.借助幾何畫板操作觀察，我們可以發(fā)現(xiàn)，O′B′與雙曲線的交點(diǎn)在第一象限內(nèi)，即圖2中當(dāng)點(diǎn)O′與點(diǎn)A重合時(shí)，對(duì)應(yīng)t取到最小值4；圖3中當(dāng)點(diǎn)B′剛好落在雙曲線上時(shí)，對(duì)應(yīng)t取到最大值.此時(shí)過(guò)點(diǎn)B′作B′H⊥x軸于點(diǎn)H，在等邊△BPB′中，設(shè)BH=a，則B′H=a.于是點(diǎn)B′的坐標(biāo)為（a+2，a），代入雙曲線的解析式得方程a（a+2）=4，解得a=－1±，這里取a=－1+，負(fù)值舍去，所以BP=2BH=2a=－2+2，于是OP=OB+BP=2+（－2+2）=2，此時(shí)取得t的最大值為2.

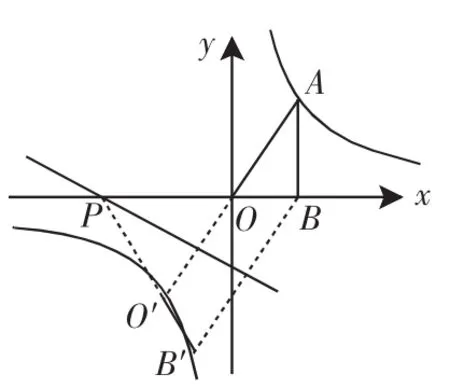
圖4

結(jié)論：交點(diǎn)在第一象限內(nèi)時(shí)，t的取值范圍是4≤t≤2.當(dāng)O′B′與雙曲線的交點(diǎn)在第三象限時(shí)，如圖4，點(diǎn)O′在雙曲線上時(shí)，對(duì)應(yīng)t取到最小值；點(diǎn)B′在雙曲線上，對(duì)應(yīng)t取到最大值.具體數(shù)值可以根據(jù)雙曲線關(guān)于原點(diǎn)中心對(duì)稱，結(jié)合本題的軸對(duì)稱的性質(zhì)得到t的最小值為－2，最大值為－4.當(dāng)然也可以類似于第一象限內(nèi)的求法，有興趣的讀者不妨試試.總之，交點(diǎn)在第三象限內(nèi)t的取值范圍是－2≤t≤－4.

綜上所述，當(dāng)O′B′與雙曲線有交點(diǎn)時(shí)，t的取值范圍是4≤t≤2或－2≤t≤－4.

說(shuō)明：第（2）題的解題思路比較復(fù)雜，同時(shí)又是一個(gè)動(dòng)態(tài)問(wèn)題，用到了分類討論的思想，解題過(guò)程中應(yīng)用了待定系數(shù)法求一次函數(shù)、反比例函數(shù)的解析式，同時(shí)考查對(duì)勾股定理、解二元一次方程組、解不等式、含30度角的直角三角形的性質(zhì)、三角形的內(nèi)角和定理、根的判別式等知識(shí)點(diǎn)的理解和掌握，能綜合運(yùn)用這些性質(zhì)進(jìn)行計(jì)算是解答此題的關(guān)鍵，此題是一個(gè)拔高的題目，有一定的難度.

思考：這是一道中考填空題的最后一題，顯然有一定的難度，而對(duì)于填空題一般只是提供參考答案，無(wú)法得知解題的思路，通過(guò)百度文庫(kù)搜索，可以查到該份試卷的解析版，讀者可以從網(wǎng)上查閱，其中本題的參考答案中計(jì)算量相當(dāng)大，計(jì)算難度較高，所列的直線O′B′的解析式相當(dāng)復(fù)雜，關(guān)于判別式Δ≥0的不等式難度更大，如果能較好地結(jié)合幾何圖形的性質(zhì)進(jìn)行解題，將能大大減少計(jì)算，起到事半功倍的效果.本文所提供的解法，就能較好地體現(xiàn)解題的優(yōu)越性，同時(shí)滲透數(shù)形結(jié)合這一重要的數(shù)學(xué)思想.