有效利用數(shù)學(xué)錯題集，培養(yǎng)學(xué)生的思維品質(zhì)

☉江蘇省栟茶高級中學(xué) 張 飛

錯題集是學(xué)生在學(xué)習(xí)過程中，把自己做過的作業(yè)、習(xí)題、試卷中的錯題整理成冊，便于找出自己學(xué)習(xí)中的薄弱環(huán)節(jié)，在復(fù)習(xí)時能夠突出重點、更有針對性，進(jìn)而提高復(fù)習(xí)效率、提高學(xué)習(xí)成績.本學(xué)期筆者嘗試指導(dǎo)學(xué)生使用錯題集來搜集典型錯題，通過錯題集進(jìn)行數(shù)學(xué)反思、培養(yǎng)學(xué)生良好的學(xué)習(xí)態(tài)度和習(xí)慣，指導(dǎo)學(xué)生學(xué)會歸納分析、梳理，抓住問題的關(guān)鍵，條理化、系統(tǒng)化地解決問題；通過錯題集解決零散、疏漏等問題，通過一學(xué)期的實踐，有效使用錯題集，可以培養(yǎng)優(yōu)良數(shù)學(xué)思維品質(zhì)，具體表現(xiàn)為思維的嚴(yán)密性、廣闊性、深刻性、獨創(chuàng)性及批判性等數(shù)學(xué)思維品質(zhì).

一、經(jīng)常閱讀，查漏補缺，培養(yǎng)數(shù)學(xué)思維的嚴(yán)密性

錯題集不是簡單的錯題的集中，它需要學(xué)生經(jīng)常把其中的錯題拿出來復(fù)習(xí)，重新再做，體會其中的方法，這樣就使每一道題都發(fā)揮出最大效果，在今后遇到同類習(xí)題時，就避免在同一個地方摔倒.這樣經(jīng)常溫故知錯、持之以恒，學(xué)生的成績就會得到提高.

案例1 （1）△ABC中，A（0，-1），B（0，1），A，B，C所對的邊分別為a，b，c，且a，c，b構(gòu)成公差大于0的等差數(shù)列，則頂點C的軌跡方程為______.

學(xué)生都能解出方程，但忽視了限制條件：能構(gòu)成三角形而且公差大于0.

（2）對概念學(xué)習(xí)的反思.

生1：今天學(xué)習(xí)了橢圓的定義，我用代數(shù)式表示：

E（-2，0），F(xiàn)（2，0），EF=4，令P（x，y），則

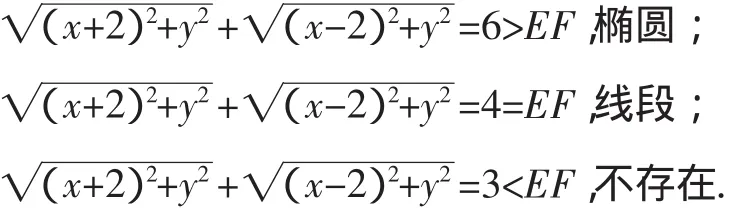
（3）對出錯題的反思.

又1+2+22+…+210有11項，

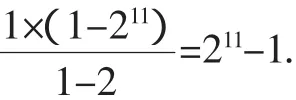
讓學(xué)生整理錯題集，一方面可以完善學(xué)生對知識的理解，拓寬學(xué)生的思維方式，提高解題能力，另一方面，老師通過閱讀學(xué)生的錯題集，了解學(xué)生的學(xué)習(xí)情況，及時調(diào)整教學(xué)計劃，同時促進(jìn)師生之間的交流.

二、相互交流，必要補充，培養(yǎng)數(shù)學(xué)思維的廣闊性

由于基礎(chǔ)不同，每個學(xué)生的錯題集各不相同.通過交流，學(xué)生之間可以相互借鑒，提醒自己不要犯同樣的錯誤，提高做題的效率.

生3的錯誤解法：設(shè)F1（-c，0），F(xiàn)2（c，0），在△F1PF2中用余弦定理，得到：

化簡得：

對①式兩邊平方，化簡得c2=4或16.再由點在橢圓上，解出a2，b2的值.

事實上，①式隱含了條件16-2c2≥0，所以c2=16舍去.在整理錯題時可以注明，化簡的過程要等價，另外，還可以補充其他同學(xué)的做法.

生4：設(shè)PF1=m，PF2=n，由橢圓的定義及在△F1PF2中用余弦定理得：

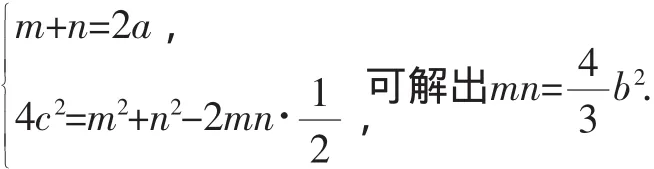
由①，②可解出a2=10，b2=6.

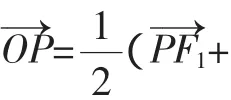
當(dāng)然，生3的錯誤對其他同學(xué)也是個警示，其他同學(xué)也可以把他的錯誤標(biāo)注在自己的錯題集上.

對于每一個錯題，你應(yīng)該能從各個方面理解它，補充多種解法，否則，在下一次測試中，對于這一問題的處理再深入一點，你可能還要犯同樣的錯誤.

三、注重聯(lián)系，聯(lián)想轉(zhuǎn)化，培養(yǎng)數(shù)學(xué)思維的深刻性

在教學(xué)活動中，學(xué)生對很多數(shù)學(xué)問題無從下手.學(xué)生訂正錯題后，此時的關(guān)鍵是教師如何讓學(xué)生的思維逐步上升到能揭示知識間內(nèi)在的本質(zhì)屬性.所以在做錯題集的過程中，培養(yǎng)學(xué)生善于洞察數(shù)學(xué)對象的本質(zhì)屬性及相互關(guān)系；善于消去條件與結(jié)論的本質(zhì)差異，尋找解決問題的突破口，迅速確定解題策略并形成解題方法，即培養(yǎng)學(xué)生數(shù)學(xué)思維的深刻性.

CRD法雖然已經(jīng)被廣泛地應(yīng)用于大斷面淺埋偏壓隧道的建設(shè)，但仍存在一定的技術(shù)問題，主要包括施工指導(dǎo)問題和防排水技術(shù)問題，這或多或少地導(dǎo)致大斷面淺埋偏壓隧道建設(shè)存在一些問題。

學(xué)生在訂正題后，可以引導(dǎo)學(xué)生聯(lián)想到，若把雙曲線改為橢圓，則以PF1為直徑的圓和哪個定圓相切？

通過引導(dǎo)，看似不同的題目，其解決的方法和思想都是一樣的，都可以用圓錐曲線的定義來解決.由此可見，學(xué)生訂正完一道題后，會經(jīng)常注意反思此題的思想方法是否可以做一般性的推廣與引申，長此以往，學(xué)生可以鞏固他們的知識和發(fā)展他們的解題能力，形成數(shù)學(xué)思想，提高解題能力，同時培養(yǎng)了數(shù)學(xué)思維的深刻性.

四、錯題改編，善于思考，培養(yǎng)數(shù)學(xué)思維的獨創(chuàng)性

這一工作的難度較大，解題經(jīng)驗豐富的同學(xué)可能做起來比較順利.很多同學(xué)在解了很多題目之后，對有些題型能夠準(zhǔn)確把握.初始階段，學(xué)生只需要對題目做一點改動.如：考慮條件與結(jié)論交換是否成立？考慮一般的情況會怎樣？

案例4 已知直線y=x-2與拋物線y2=2x相交于點A，B，則∠AOB=_____.

學(xué)生在訂正完后，可以引導(dǎo)學(xué)生將此題改編：

將直線一般化：

（1）直線l過（2，0），交拋物線y2=2x于A，B兩點，則∠AOB=______.

將條件與結(jié)論交換，證明充要性：

（2）已知直線l交y2=2x于A，B兩點，且OA⊥OB，證明：直線l過（2，0）.

將結(jié)論一般化：

（3）已知直線l交y2=2px（p>0）于A，B兩點，且OA⊥OB，證明：直線l過（2p，0）.

將點O位置一般化：

（4）已知直線l交y2=2px（p>0）于A，B兩點，M是拋物線上一點，且MA⊥MB，證明：直線l過定點.

在學(xué)生做錯題集的過程中，只要學(xué)生的思考方式方法新穎，獨特，教師應(yīng)該不吝表揚，鼓勵學(xué)生善于動腦，培養(yǎng)學(xué)生思維的獨創(chuàng)性.

五、典型錯誤，善于積累，培養(yǎng)數(shù)學(xué)思維的批判性

開始錯題集里淺顯的錯誤會占大多數(shù)，隨著錯題的積累，錯題集中的錯誤層次會越來越高.

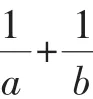
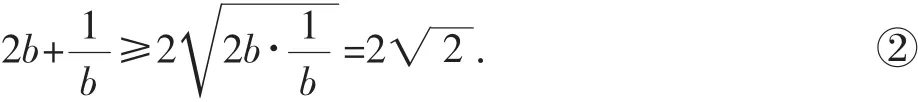
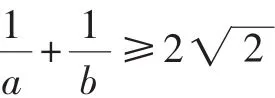
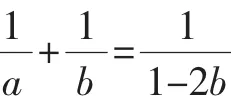
學(xué)生通過積累典型錯誤，發(fā)現(xiàn)在前3種解法中都無法取到等號，只有解法4的答案是正確的.從中還總結(jié)利用基本不等式求最值要注意的問題：“一正、二定、三相等”.這樣通過錯題集，學(xué)生自己不斷積累錯誤，加深學(xué)生對易錯地方的印象，避免錯誤的再次發(fā)生.

又如，學(xué)生在求定義域，值域時總漏掉一些函數(shù)本身固有的范圍，如指數(shù)函數(shù)，對數(shù)函數(shù)，三角函數(shù)等；在求離心率時會忘記要與橢圓或雙曲線本身的范圍取交集；當(dāng)一個集合為某一集合的子集時總是不考慮空集的情況等.這些問題只要平時多積累，考試時就不容易犯錯.

錯題集是提高學(xué)習(xí)效率的辦法.通過錯題集的使用，可以提高思維質(zhì)量，可以更準(zhǔn)確地把握知識點及概念，可以極大地改善粗心的現(xiàn)象，可以迅速地提高學(xué)習(xí)成績，有效地進(jìn)行數(shù)學(xué)反思.

總之，重視學(xué)生錯題集的建立是基于學(xué)生的思維實際，避免老師全盤灌輸，讓學(xué)生將自己的數(shù)學(xué)思維方式在錯題集上顯現(xiàn)出來，讓學(xué)生自己主動整理，糾錯，反思，從而培養(yǎng)學(xué)生優(yōu)良的數(shù)學(xué)思維品質(zhì).