賽場命題天然成 真題真解真思想——2013年全國高中數學聯賽湖北省預賽填空題詳解

☉湖北省浠水縣實驗高級中學 程賢清 占巧月

2013年全國高中數學聯合競賽湖北省預賽試卷分高一年級卷和高二年級卷，每份試卷均設計10道填空題和3道解答題.命題組提供的參考答案對填空題只給出結果，未做詳解.為了幫助同學們在學習、研究中有所啟發和參照，本文對高二試卷中所有填空題做出詳解分析和點評.

分析：由集合C中代表元素為a+b，且a∈A，b∈B，可用列舉法寫出集合C={3，5，7，9，11，13，15，19，21，23，25，27}，從而集合C的所有元素之和為（3+5+7+…+27）-17=195-17=178.

點評：本題考查了考生對集合概念的本質理解及計算的靈活性.易錯點有：①未去掉生成集合C時的重復元素；②不會轉化為等差數列求和.

2.已知數列{an}滿足：a0=0，a1=1，且a2n=an，a2n+1=an+1（n∈N*），則a2013=_________.

分析：由遞推關系可知，無論下標為奇數還是偶數，都可以迅速將下標縮小.據此，反復使用遞推關系，即可求得結果.a2013=a1006+1=a503+1=a251+2=a125+3=a62+4=a31+4=a15+5=a7+6=a3+7=a1+8=9.

點評：本題重點考查了轉化思想和解題方法的選擇判斷能力.本題易錯點有：①欲求出通項，思路受阻；②平時訓練過此類題，大多是周期數列，因而部分考生很想求出該數列的周期，但由于此題無法求出周期（本不是周期數列）而出現思路中斷；③不了解a0這個條件怎么用，產生畏懼心理.實際上這里a0是數列的首項，a1是數列的第二項.設置a0的目的是考查考生解題的抗干擾能力.事實上本題去掉a0=0這個條件，不影響解題結果.

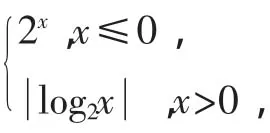
分析：由已知得F（1，0）.設P（x，y），M（x0，y0），則過點M的切線方程為集為_________.

點評：本題主要考查分段函數的概念，指數、對數、絕對值的運算及分類討論思想.本題易錯點是對數及其絕對值的運算.

點評：本題考查的知識有同角三角函數關系，二倍角公式，正弦函數有界性，二元均值不等式.考查的方法是利用均值不等式及正弦函數的有界性進行連續放縮.該法能夠成功的關鍵在于多次放縮時，等號能同時成立.本題易錯點是不能合理分組進行連續放縮.

有P=2cos2x-2cos2y-4cosx+4cosy

=2（cosx-1）2-2cos2y+4cosy-2

≥-2cos2y+4cosy-2=2cosy（2-cosy）-2＞-2.

又有P=2（cosx+cosy-2）（cosx-cosy）＜0.

綜上所述，有P∈（-2，0）.

點評：本題主要考查余弦函數的單調性、二次函數的性質以及三角恒等變換、放縮變換的能力.解題難點是所求范圍的兩個界點需要用兩種不同的思路進行求解.本題易錯點是不能準確求出兩個界點值，導致所求范圍擴大.

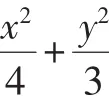
圖1

①-②×4得（x0-4）（x-4）=0.又-2≤x0≤2，

故x-4=0，即x=4為所求點P的軌跡方程.

點評：本題考查了橢圓的切線方程、向量的數量積等知識以及代數的消元變形能力.易錯點是列出相關條件方程后不知如何變形運算.

7.從集合A={1，2，3，…，30}中取出5個不同的數，使這5個數構成等差數列，則可以得到不同的等差數列的個數為_____________.

分析：按公差分別為1，2，3，…，7進行分類（先考慮公差為正數的個數）：

公差為1的等差數列有1，2，3，4，5；2，3，4，5，6；…；26，27，28，29，30.共26個.

公差為2的等差數列有1，3，5，7，9；2，4，6，8，10；…；22，24，26，28，30.共22個.

……

公差為7的等差數列有1，8，15，22，29；2，9，16，23，30.共2個.

故構成公差為正數的不同等差數列的總個數為26+22+18+…+6+2=98.

又公差為負數的不同等差數列的個數也為98.

故所求不同的等差數列的個數為98×2=196.

點評：本題主要考查集合及等差數列的概念，數列求和等知識和分類討論的策略和意識.本題易錯點是易漏掉計算公差為負數的情形.

8.四面體P-ABC的體積為1，G和K分別是△ABC和△PBC的重心，過G作直線分別交AB，AC于點M，N，那么四棱錐K-MNCB的體積的最大值為__________.

分析：如圖2，連接PK并延長交BC于Q，過P作PO⊥面ABC，垂足為O，連接OQ.由PO⊥面ABC知面POQ⊥面ABC，過K作KR⊥OQ于R，則KR⊥面MNCB，KR為四棱錐K-MNCB的高.記四面體P-ABC的底面積為S，高PO=h.

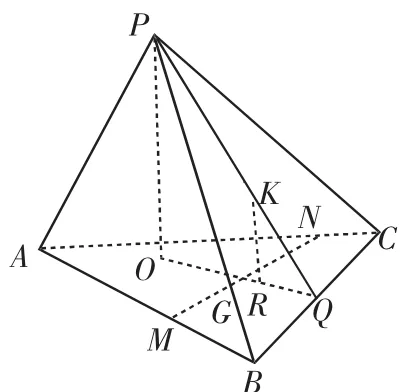
圖2

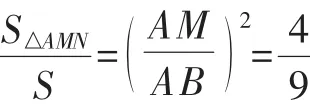
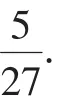
點評：本題是一道立體幾何綜合題.重點考查了空間問題平面化策略以及運動變化思想的應用.涉及的幾何知識有：重心概念及重心定理，相似三角形的有關性質，棱錐的體積公式.本題易錯點有：①不能準確畫出空間圖形或畫出的圖形粗糙，線條重疊，妨礙思考；②不善于運用平面化的策略及運動變化思想對問題進行逐步簡化.

9.已知互不相等的三個實數a，b，c成等比數列，且logca，logb c，logab構 成 公 差 為d的 等 差 數 列 ， 則d=__________.

分析：因為a，b，c成等比數列，所以b2=ac，兩邊同取以b為底的對數得：

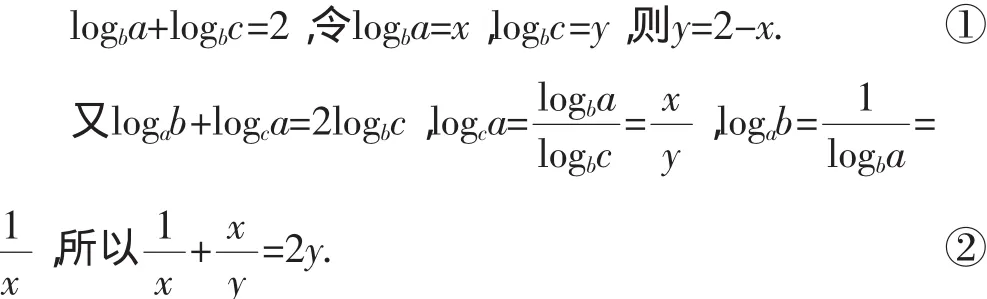
①代入②整理得2x3-9x2+9x-2=0.

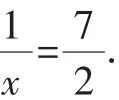
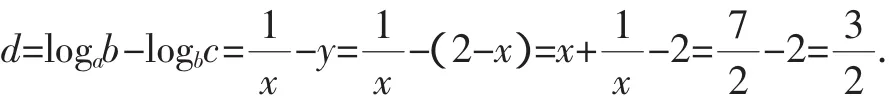
點評：本題是高一試卷中的解答題12題，此處最后兩步運用整體思想處理較命題組參考答案的解法更為簡捷，有效地避免了直接解方程再分類討論的煩瑣運算.

本題考查了等差數列、等比數列的概念，對數的運算性質，換底公式等知識，還考查了換元（簡化）轉化，整體代入等重要數學思想方法.結合式的運算對考生思維能力和運算技巧的結合進行了深刻考查.試題設計精巧，下手易，深入難.解決本題的關鍵有：①是對b2=ac兩邊取對數；②是對已知對數式換元.本題易錯點是根據已知條件直譯列出方程后不知如何運算，換元轉化意識不強.

10.已知a，b，c，d∈［-1，+∞），且a+b+c+d=0，則ab+bc+cd的最大值為_______.

分析：本題為多變元求最值問題，可嘗試逐步消元（減元）.比如，消去d得，ab+bc+cd=ab+bc-c（a+b+c）=abac-c2=a（b-c）-c2.為便于放縮，繼續消元，可對b，c的大小關系進行分類討論.

（1）若b≤c，則由a≥-1，b-c≤0知a（b-c）≤-（b-c）有

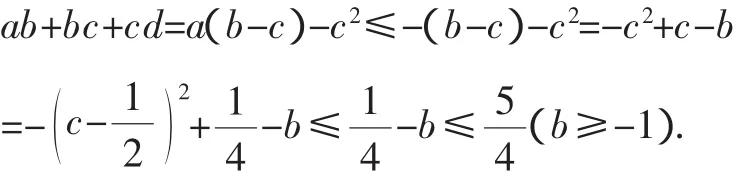
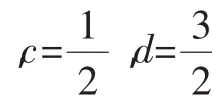
由d≥-1，c-b≤0知d（c-b）≤-（c-b），

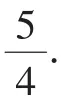
點評：本題是一道區分度較大的難題，競賽味濃.著重考查考生的代數推理能力 （尤其是不等式的放縮變形能力）.本題易錯點是放縮變形方向不明.本題的放縮技巧很值得我們思考與回味.