“研究”與“成長”齊飛 秋水共長天一色——談命題研究與教師的專業化成長

☉江蘇省南通市通州區金沙中學 喻國勇

數學命題研究，是數學教師的一項基本工作，是日常教學工作的延伸.十年前，筆者剛開始工作時，對高中數學教學的理解限于：教學、解疑、升學，從來沒覺得研究命題是數學教師的分內之事． 在經歷了教材改革和課程改革后，筆者漸漸從當年的青年教師慢慢成長起來，現在每每看到新的問題總是覺得自己的知識是多么的淺薄！正如一位哲人說：“人的知識好比一個圓內的部分，圓的外部都是我不懂的知識，每當自身知識越多時，圓就會越大，圓周與外界接觸（即不懂的知識）也越大，從而不知道的東西也更多.”說得太好了，教學十年，筆者在教學之路上的不斷摸索，得到的體驗是一方面研究數學命題有利于提高教學質量、優化課堂效率；另一方面對命題的研究也大大加快了教師的專業化成長，本文通過這些年的親身體驗談談高中數學命題研究和教師的專業化成長．

一、命題研究的背景

對數學命題的研究是一位中學教師在擁有多年教學經驗后慢慢堆砌而成的，優秀的數學教師不僅在高效課堂教學等方面出類拔萃，還能在對數學命題的研究上有所建樹.近年來，對數學命題的研究也取得了一定的成果，諸如文［1］～［4］等，筆者拜讀后發現此類文章在對命題的構成、命題的心理機制、高觀點下的命題思路等做出了一定的分析和闡述.

從新課程背景的角度來看，課程教育改革和高考試題都在向“以人為本”的方向發展，要求學生掌握適合其自身發展的數學，即所謂因材施教，數學教學更注重生活化、應用化，加強課程內容、考題與生活實踐、社會科學之間的聯系.在這樣的背景下，教師對命題的研究需要與時俱進，比如許多新增加的知識板塊，如三視圖、推理證明、矩陣變換、算法等都是可以進行深度的挖掘，這順應新課程改革的方向．

從試題研究的角度來看，很多命題都有深厚的高等數學背景，用當今很流行的一句話來說——“高觀點下的初等數學”．常常可以見到很多地區的教研活動，專家對近年高考試題的背景進行解讀．因此，在這樣的背景下，教師對命題研究往往更高瞻遠矚，有針對性、普遍性和獨特性，如凸函數、李普希茲條件、不動點理論、拉格朗日定理等，從這些背景深厚的高等數學中能參悟高考數學問題的本質，有“會當凌絕頂，一覽眾山小”的感覺．

從知識交匯、教學銜接的背景來看，命題研究往往對教學指導有重要的作用，一方面在于高考試題的命制往往在于知識的交匯處，一個試題含高中數學的多個知識點組成，有利于把握教學的方向，有利于對知識進行整合，提高復習的效率；另一方面來看，初等數學與學生即將接觸的高等數學的思想方法是完全不同的，從這些命題中挖掘高等數學的影子，使其與初等數學做好銜接、相溶，有利于數學知識間的平穩過渡，對進一步的深入學習有重要的支撐．

本文將所研究的數學命題界定為：具有一定深度及高等數學背景的數學試題，這類問題不是直接引入高等數學的定理、概念，而是顯示了高等數學對初等數學的指導作用，是命題專家的偏愛，對這類問題進行深度的分析、編譯、融合，才能對中學數學教學有一定的指導意義．

二、命題編制的原則

數學考查的總要求是由考試大綱與課程標準決定的，在命題編制時如何將知識、方法、能力的要求具體貫徹到實際試題中去，是依據一定的準則進行操作的，即所謂命題原則．教師在研究命題的時候，有必要研究命題的原則，特別地，高等數學背景下試題的編制要求更高，因此筆者認為命題的編制必須關注以下原則：

1.新穎性原則

新穎性（即與時俱進）是命題命制的特點之一．命題命制的新穎性可以從兩方面來看，一方面是背景、情境的新穎，這類問題編制較為容易，只要給數學形式化的結果披上與時俱進的外衣即可；另一方面是需要高等數學為背景的試題編制，立意新穎、充滿生命力，對它的研究需要教師多年的專研（即教師專業化的成長），另外還可以從題型結構、提問方式等方面入手．如：

A．D（x）的值域為｛0，1｝

B．D（x）是偶函數

C．D（x）不是周期函數

D．D（x）不是單調函數

說明：問題的背景是狄利克雷函數，高中數學對其中的認知是定義域為R，值域為｛0，1｝，偶函數，無法畫出函數圖像，無最小正周期；從深層次的背景來說，狄利克雷函數處處不連續、不可導，是可測函數，在任何區間內黎曼不可積，了解其更深層次的知識有利于提高教學的效率．

2.科學性原則

命題編制的科學性是一個試題最基本的原則，它要求教師從一個解題者到變式研究者再到創新者之間慢慢的成長，在模仿、學習和創新之間學會編制問題的科學性、正確性、邏輯性、簡潔性等，在充分考慮問題入口寬廣、解法可行的基礎上，不與中學數學的定理、概念產生矛盾，不與將來高等數學內容發生沖突．如：

案例2（浙江省模擬卷）將3個完全相同的小球隨機地放入編號依次為1，2，3，4，5的盒子里，用隨機變量ξ表示有球盒子編號的最大值．

（1）求P（ξ=2）；（2）求 ξ的分布列和數學期望Eξ．

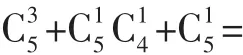
（2）同理，ξ的分布列如下表：

?

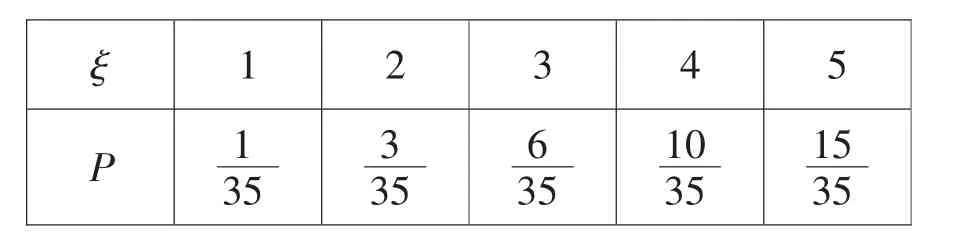
數學期望Eξ=4．

3.選拔性原則

高考是選拔性考試，必然要求命題者對考題層次有區分度，以便選拔數學素養較高的人才，因此在命題上，選拔性的試題對學生的區分度是較大的，此類命題的得分點往往呈現正態分布，數學素養較高、能力較強的學生基本能解決，對于大部分學生而言，此類問題只能嘗試或者解決部分，重在對學生智能水平和數學素養的考查，立足于進行公平、公正的選拔.如：

圖1

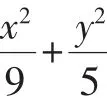
（1）設動點P滿足PF2-PB2=4，求點P的軌跡；

（3）設t=9，求證：直線MN必過x軸上的一定點（其坐標與m無關）.

三、命題研究與教師專業化成長的關系

筆者在教學研究的道路上不斷嘗試，認識到一方面研究數學命題有利于提高教學質量、優化課堂效率；另一方面對命題的研究也大大加快了教師自身專業化的成長，下面簡述兩者之間的關系.

1.命題研究推動教師數學素養的提升

數學與其他學科的不同在于除研究對象之外，最突出的就是數學對象的內部規律真實性與表象背后的本質屬性，必須用邏輯推理的方式來證明.因此，數學命題的研究需要一定的數學知識、數學內涵和學習的耐心，這其中隱含的數學素養對教師自身發展上有較大的決定性作用.

數學課程內容的絕大部分都可以說是數學命題，數學課程的核心內容就是由數學命題組成的.我們在數學教學的整個階段中都離不開數學命題，要學運算，離不開運算法則，從運算中提高教師的計算能力；要計算圖形的面積、體積，必然離不開數學公式，加強對公式的熟練運用并能融會貫通；要學習數學證明，必然先介紹公理，而后再有定理和推論，培養教師思維的嚴謹性；對命題變式的研究，大大提高了教師在數學知識點交匯處演變問題的能力；對一個高考試題的背景分析、探討和學習，能迅速提升教師看待中學數學問題的高度；對優秀命題進行總結和反思，大大提升了教師科研的水平和能力.因此數學命題的研究推動著教師的成長.

2.教師的專業化成長離不開命題研究

教師的成長離不開對數學命題的研究.對數學命題研究的本質是對一個問題的深層次思考，即反思.從再認知理論的角度來說，荷蘭數學教育家弗賴登塔爾指出：數學學習是一種再創造學習，反思是數學思維活動的核心和動力.筆者認為利用“再創造學習理論”進行的命題研究，一方面回顧問題中出現的基本知識，另一方面通過變式等研究對知識進行了重組，從而優化了知識在腦海中存儲，久而久之，產生的東西便可促進教師的成長.

從建構主義的角度來看，教師的成長不能僅限于中學數學本身的學習經驗、解題心得，應該不斷嘗試用自己頭腦中的模式去建構對問題的理解（即模式識別），不同的教師對問題的看法是不盡相同的，所以對數學命題再次建構是比較有效、快捷的學習方式.筆者曾經嘗試此類數學命題的建構，采用的是研究性學習的模式，既提高研究的水平也促進了自身的發展.下面給出一個筆者歷經多時的命題研究案例：

案例4 （2009年河南省數學競賽）已知拋物線C：y2=4x，以M（1，2）為直角頂點作該拋物線的內接直角三角形MAB（如圖2）.

（I）求證：直線AB過定點；

圖2

（II）過點M作AB的垂線交AB于點N，求點N的軌跡方程.

（1）命題解法的研究.

針對本題最常見的學生解題心理機制：

①設出A、B兩點坐標，利用垂直關系將直線AB用點坐標表示即可；

②考慮到直線AB斜率不為0，設直線AB方程：x=my+b，利用垂直關系及韋達定理；

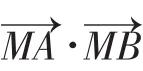
（2）命題思想方法的研究.

①主要思想：數形結合思想、方程思想，運算中要注意“設而不求”；

②考慮到直線AB斜率不為0，設AB直線方程為：x=my+b，聯立拋物線方程，利用韋達定理；

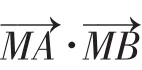
④至于第（II）問，由第（I）問搭建的“腳手架”順勢而行，點N的軌跡必在點M和定點（5，-2）為直徑的圓上.

設出直線方程與拋物線聯立，并結合垂直關系的向量式，適合解決一般圓錐曲線和直線位置關系的問題，具有推廣性.另外，對思路①、③，可以做適當引導.

以上兩點是筆者嘗試的基本命題研究，隨著后來對文［7］的學習，有了下面更進一步的研究：

（3）命題的背景研究.

如圖2，將問題變式，過定點（5，-2）的動弦交拋物線于A、B兩點，作MA⊥MB，則M點的軌跡是什么？顯然是圓，該圓與拋物線的交點就是原題中的M（1，2）.

若將定點（5，-2）變為拋物線的焦點，過焦點作動弦交拋物線于A′、B′兩點，過A′、B′分別作拋物線的切線，設切線交于M′，則△M′A′B′即為阿基米德三角形.容易驗證三個性質：

①M′A′⊥M′B′；

②M′必在拋物線準線上；

③M′F⊥A′B′.

關于阿基米德三角形的性質很多，文［7］已總結過，有關此三角形的高考試題也比較多，各省市近年均圍繞阿基米德三角形進行過試題編制，如：2008年山東卷第22題，2007年江蘇第19題，2006年重慶第22題，2005年江西第22題，2006年全國卷Ⅱ第21題等.

在學習了文［8］之后，筆者自身的知識得到了拓寬，對命題得到了新的研究.

四、結束語

隨著課程改革的深入和不斷變革的高考，將來的數學教育應該著重向應用、能力化的方向發展，勢必要求教師自身擁有更扎實的基本功、更全面的知識、更高人一籌的研究能力，以計算機輔助教學來說：多年前PPT是CAI的主流，近年來，幾何畫板、超級畫板、Cabri3D、Flash等越來越普遍使用在教學中，更為專業的如Mathematica、MathCAD等也在慢慢滲透進數學教學中來，教師也要用與時俱進的研究來帶動自身的成長，我們將來的教育極有可能和歐美發達國家一樣，更注重能力的考查.借本文與讀者共同努力，不斷發展.

1.鄭慶全.數學命題教學研究［J］.山東教育學院學報，2007（5）.

2.石志群.高考數學命題思路分析及復習策略［J］.中學數學月刊，2009（11）.

3.張夏強.數學名題在高考命題中的應用［J］.中學數學教學，2011（1）.

4.肖凌戇.關注探究創新 考查理性思維——基于數學創新意識的高考命題特點［J］.中國數學教育，2011（10）.

5.沈恒.辨基本事件，觀概率教學［J］.中學數學教學參考（上旬），2012（1）.

6.張琥.例析以高等數學為背景的高考數學試題［J］.中學數學（上），2012（4）.

7.吳躍生.再談拋物線的阿基米德三角形的性質［J］.數學通訊，1999（8）.

8.吳波.也說蝴蝶定理的一般形式［J］.數學通報，2012（6）.