基于ABAQUS的鋼筋混凝土結構懸臂梁跨高比的分析研究
黃 輝,陳 韋,彭杰波,黃 丹,廖文遠
(1.長沙理工大學土木與建筑學院,湖南長沙410114;2.江蘇省張家港市建筑設計研究院有限責任公司保稅區分公司,江蘇張家港215600;3.華南理工大學土木與交通學院,廣東廣州510640;4.昆明理工大學建筑工程學院,云南昆明650504)
1 工程實例
鋼筋混凝土懸臂梁結構可以使建筑體型獨特、外觀新穎、增加有效的上部利用空間。在實際工程中應用廣泛,多用于挑檐、陽臺、雨棚以及屋頂等。
中元·鉑金灣幼兒園如圖1所示,地處云南保山,屬三層公共建筑。抗震設防烈度八度,耐久年限為3類,耐火等級為二類,屋面防水等級為Ⅲ級。鉑金灣幼兒園利用鋼筋混凝土懸臂梁結構使建筑的室內空間得以延伸,提高內外部空間的聯系。幼兒園是讓幼兒身體、智力和心情健康發展的場所,因其特殊性,幼兒園的建筑結構設計要求更高,比如還需滿足《混凝土結構設計規范》(GB 50010-2010)[1]中對托兒所、幼兒園設計的各項要求。

圖1 中元·鉑金灣幼兒園效果圖
鋼筋混凝土懸臂梁結構設計的關鍵是跨高比的取值,現階段對于跨高比的取值規范沒有明確的規定,往往是通過經驗取值,因此在工程實際設計過程中跨高比的取值成為研究的熱點。文獻[2]及文獻[3]給出了在不同荷載集度下,集中荷載作用下鋼筋混凝土懸臂梁h/b=2~3的容許跨高比上下限值。本文運用ABAQUS非線性分析軟件以及規范規定的裂縫寬度計算公式,對懸臂梁在不同跨高比下的受力、撓度及裂縫寬度分析對比。鉑金灣幼兒園結構平面圖如圖2所示。
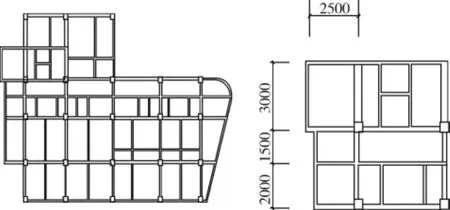
圖2 幼兒園結構平面圖
2 本構關系
2.1 計算模型的選取
混凝土采用 ABAQUS 軟件中的損傷塑性模型[4]、[5],該模型可用于單向加載、動態加載及循環加載等情況,具有較好的收斂性。采用各向同性損傷彈性結合壓縮塑性和各向同性拉伸的模式來表示混凝土的非彈性行為。鋼筋采用ABAQUS軟件中的等向強化彈塑性模型[6],滿足 VonMises屈服準則。
2.2 現行規范的有關規定
在工程實踐中結構物的裂縫形成產生的原因可分為兩類,一類是由荷載引起的裂縫,另一類是由變形因素(非荷載)引起的。由于本文中提到的跨高比上、下限值是通過《混凝土結構設計規范》中的最大裂縫寬度限值計算的,為了使多組跨高下裂縫寬度和最大裂縫寬度限值具有可比性,本模型采用《混凝土結構設計規范》(GB 50010-2010)中公式:
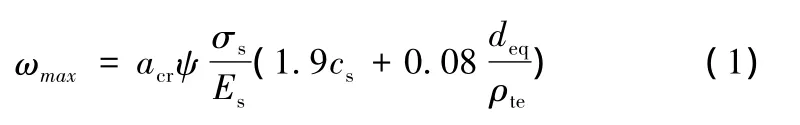
3 計算實例
3.1 計算簡圖
根據建筑物結構圖(如圖2),本棟最大懸挑長度2.5 m,經受力分析,等效于懸臂端集中荷載P=5 000 N,計算簡圖如圖3。集中荷載作用下鋼筋混凝土懸臂梁h/b=2~3的容許跨高比限值如表1。當集中荷載作用下鋼筋混凝土懸臂梁h/b=2、(Gk+Qk)/l2≤2情況,跨高比上限取8.3~8.7,下限取5.9~6.8,用ABAQUS軟件對本例懸臂梁模擬分析,選用限值范圍內的四組跨高比5、6、7、8進行比較,分析不同跨高比下結構的受力、撓度及裂縫寬度,并分析原因(考慮跨高比為單一變量定寬高比h/b=2,箍筋采用沿梁全長加密)。
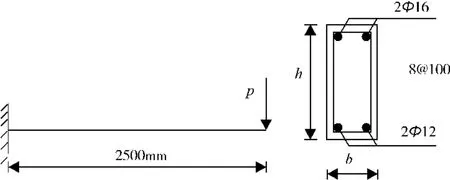
圖3 梁配筋示意
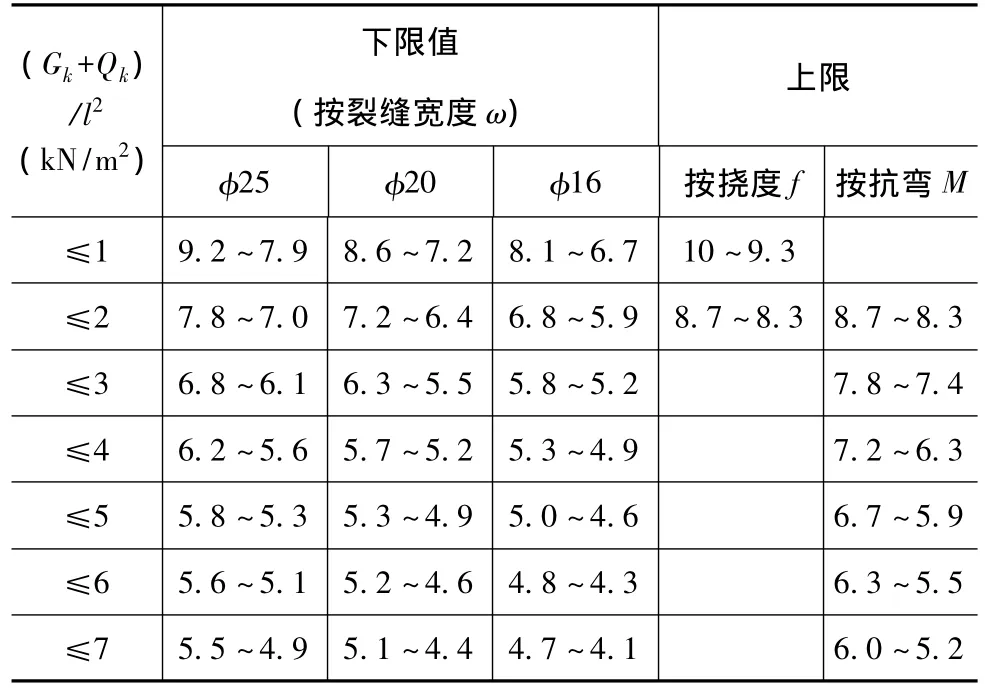
表1 集中荷載作用下鋼筋混凝土懸臂梁h/b=2~3的容許跨高比上下限值
混凝土采用C30,受力鋼筋、箍筋均選用HRB335,保護層厚度取C=35 mm,梁截面尺寸如圖3所示,混凝土、鋼筋特性及跨高比分組數據分別如表2~表4所示。

表2 混凝土特性

表3 鋼筋特性
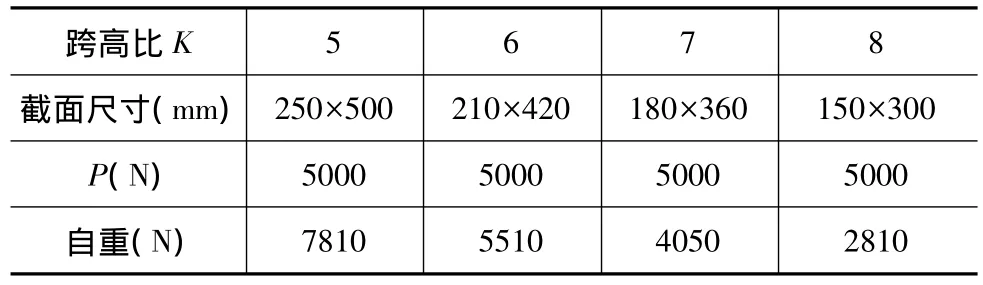
表4 跨高比分組數據
3.2 ABAQUS有限元模型的建立
本文用非線性有限元分析軟件ABAQUS建立鋼筋混凝土懸臂梁的三維有限元模型[7]、[8]。鋼筋混凝土結構的有限元模型有三種建模方式,分別是整體式模型、界面單元分離式模型和位移協調分離式模型。整體式是假定混凝土和鋼筋粘結很好,且將單元看作連續均勻材料,因此只需用混凝土單元模型,把鋼筋分布于整個單元中。界面單元分離式模型就是把混凝土、鋼筋用不同單元處理,并用彈簧單元連接,來模擬鋼筋與混凝土之間的滑移,這種建模方式能逼真的模擬鋼筋混凝土的實驗力學行為,但是建模難度大,且工作量大。位移協調分離式模型是將鋼筋與混凝土用不同單元來處理,并將鋼筋和混凝土固結在一起,忽略兩者之間的相對滑移,實驗表明當保護層厚度足夠時,設置剪切連接鍵,滑移不是問題。本文結合工程實例采用位移協調分離式方法建模。
在ABAQUS中,混凝土結構中的鋼筋可以通過鋼筋單元來實現,可以添加單獨的鋼筋單元,也可以在單元屬性中附加鋼筋屬性以組合模型的鋼筋,還可以通過Embed[9]方法將鏈桿單元或者模單元嵌入混凝土單元,Embed可以把鋼筋和主體構件分別顯示,方便對鋼筋性能的考察,本文采用Embed方法將鋼筋單元嵌入混凝土單元。
混凝土采用8節點六面體線性減縮積分的三維實體單元C3D8R,該單元計算效率高且不易發生剪切自鎖;鋼筋采用三維二節點線性桁架單元T3D2,此單元每個節點有水平和垂直兩個自由度,最終建立的懸臂梁有限單元如圖4所示。

圖4 懸臂梁單元圖
3.3 模擬結果及分析
本工程選用限值范圍內的四組跨高比進行比較,利用ABAQUS非線性軟件繪制出集中荷載作用下,四組跨高比作用下懸臂梁的應力、位移云圖如圖5~圖7。根據云圖繪制梁內混凝土最大應力、鋼筋最大應力、最大撓度曲線如圖8、圖9。
各曲線圖表明,混凝土、鋼筋應力與撓度都隨著跨高比的增大而減小,比如跨高比為5~8時,混凝土的應力最大分別對應為 1.05×106Pa、1.66×106Pa、2.59×106Pa、4.84×106Pa。由《混凝土結構設計原理》[10]可知,鋼筋混凝土懸臂梁的正截面承載能力與梁截面的高度成正比,最有效提高鋼筋混凝土懸臂梁的正截面承載力的措施就是增大梁高,比增大配筋、提高混凝土強度更加有效。
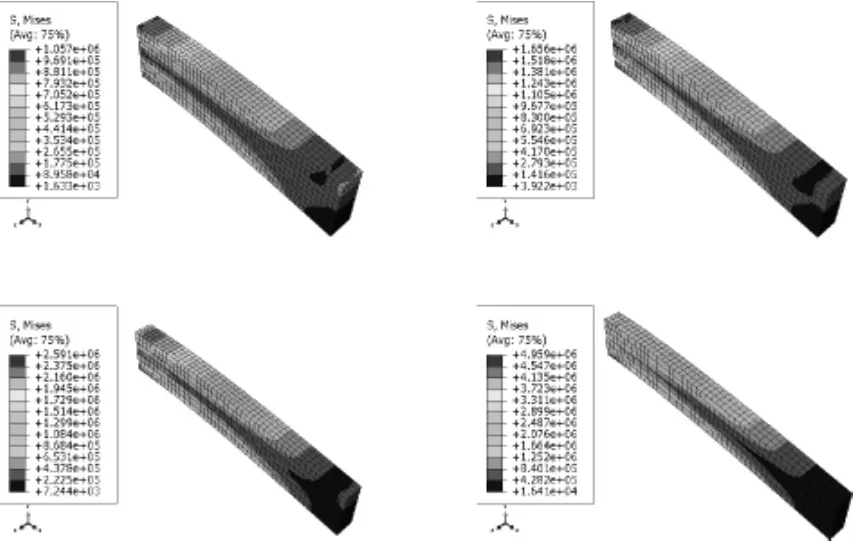
圖5 l/h=5~8混凝土的應力云圖

圖6 l/h=5~8鋼筋的應力云圖

圖7 l/h=5~8懸臂梁的位移云圖
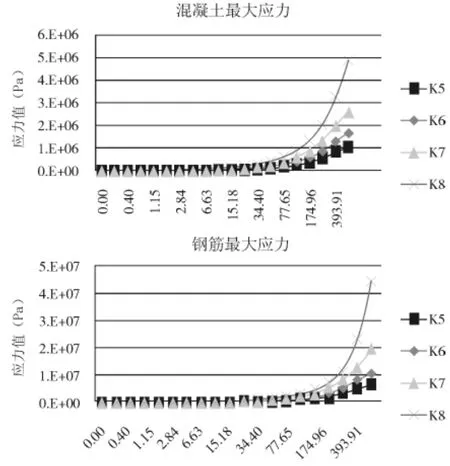
圖8 混凝土、鋼筋最大應力
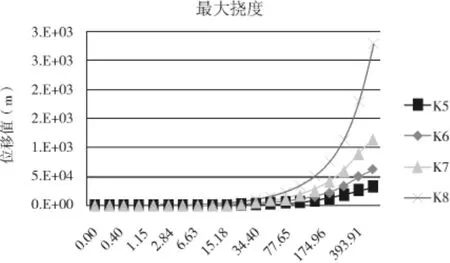
圖9 最大撓度圖
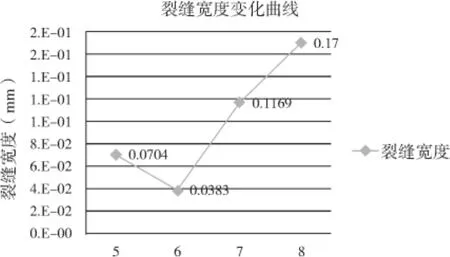
圖10 裂縫寬度變化曲線

表5 各跨高比下懸臂梁的最大裂縫寬度
由規范公式可知,在各跨高比下的裂縫寬度如表5,并繪制裂縫寬度變化曲線如圖10。圖中曲線表明當跨高比取6時,懸臂梁的最大裂縫寬度最小,這是由于跨高比的增大,雖然提高了截面剛度和強度,但是混凝土的自重也是我們在設計時需要考慮的因素。跨高比取值過大,會增大自重,使得混凝土自重成為最主要的荷載來源(表4中的自重);而跨高比取值過小時,剛度不夠,也可能使裂縫增大。
根據各類性能曲線圖與裂縫寬度表繪制出規范限值表如表6。由表可知最大裂縫寬度限值、混凝土、鋼筋最大應力與最大撓度都是滿足《規范》限值,說明文獻提供的跨高比限值是合理的。

表6 規范限值滿足情況
根據表6,規范限值采用的跨高比也僅僅只是一個范圍,設計時要根據分析計算結合裂縫的控制等級,在范圍內確定 最佳跨高比。本例對鋼筋混凝土懸臂梁受力、位移及使用性能綜合考慮,最終選定跨高比為6,即b=210 mm,h=420 mm。
4 結論
通過改變懸臂梁跨高比,分析其各項性能,從而選定懸臂梁梁截面,可以得出以下結論:
鋼筋混凝土懸臂梁的跨高比對結構有很大的影響,跨高比取值過小,會使得正截面抗彎能力和撓度滿足不了要求;取值過大,不僅自重大、造價高,而且使得裂縫寬度滿足不了要求。在集中荷載作用下,存在跨高比上、下限值,使得懸臂梁抗彎、撓度及抗裂驗算滿足規范規定。
若設計中為了滿足受力、撓度驗算,一味增加梁高,不進行裂縫寬度驗算是不合理的。
最佳跨高比的選擇,除了滿足受力、撓度及裂縫寬度規范限值之外,還要結合實際情況,比如建筑的裂縫控制等級、材料控制等等。
以上結論都是在假定鋼筋混凝土懸臂梁結構是按“強剪弱彎”設計,且有一個理想的固定端,支座處無豎向位移、轉角,在實際工程中,這些條件是否滿足尚需注意。
[1]GB50010-2010混凝土結構設計規范[S]
[2]林云云,蔣大驊.鋼筋砼懸臂梁的跨高比[J].建筑結構,1993(1):27-31
[3]Wen-zhong ZHENG,Xiao-dong WANG.Ultimatestress increase in unbounded tendons in prestressed concre tebeams[J].Journal of Zhejiang University-SCIENCE A(Applied Physics&Engineerin g),2010,11(12):998-1014
[4]石亦平,周玉蓉.ABAQUS有限元分析實例詳解[M].北京:機械工業出版社,2010
[5]雷拓,錢江,劉成清.混凝土損傷塑性模型應用研究[J].結構工程師,2008,24(2):22-27
[6]張偉,伍鶴皋,蘇凱.ABAQUS在大體積鋼筋混凝土非線性有限元分析中的應用評述[J].水力發電學報,2005,24(5):70-74
[7]胥玉詳,朱玉華,趙昕,等.雙連梁受力性能研究[J].結構工程師,2010,26(3):31-37
[8]Xiangting Su,Zhengjun Yang,Guohua Liu.FINITE ELEMENT MODELLING OF COMPLEX 3DSTATIC AND DYNAMIC CRACK PROPAGATION BY EMBEDDING COHESIVE ELEMENTS IN ABAQUS[J].Acta Mechanica Solida Sinica,2010,23(3):271-282
[9]劉林林,屠永清,葉英華.基于ABAQUS的鋼管混凝土L形柱有限元分析[J]. 沈陽工業大學學報,2011,33(3):349-354
[10]沈蒲生.混凝土結構設計原理[M].北京:高等教育出版社,2007

