BP 神經網絡在匯率預測中的應用

徐緣圓

（中南財經政法大學，湖北 武漢 430079）

一、研究背景與研究方法

所謂匯率（又稱外匯利率，外匯匯率或外匯行市），是指兩種貨幣之間的對換的比率，同時也可視為一個國家的貨幣對另一種貨幣的價值。匯率與一國進出口、物價、資本流出入都有著密不可分的關系，會因為利率、通貨膨脹、國家的政治和每個國家的經濟等原因而變動。根據國際貨幣制度的演變，匯率可以劃分為固定利率和浮動利率。在Bretton Woods system 崩潰后，世界上匯率制度漸漸變成以浮動匯率制度為主，匯率變動更是顯現出動態化和復雜化的特征。特別是在全球經濟一體化的背景下，各國之間的聯系日益密切，相互之間的依賴性也越來越強，匯率，自然地成為各國之間經濟往來的橋梁。然而，各國的外匯管理和貨幣政策的實施效果受到了匯率的變化的嚴重干擾。在此背景下，探尋人民幣兌美元匯率的變化特征以及其內在的運行規律，對匯率進行準確的預測就有了諸多現實意義。

對匯率預測方法的研究主要有技術分析和基本分析。以基本分析方法為基礎的匯率預測應用非常之廣，其中包括很多很經典的方法理論，比如，以購買力平價理論、利率平價理論、資產市場組合模型為代表的傳統的匯率理論及模型，以基于新開放宏觀經濟學的匯率理論、混沌分析理論、基于檢驗外匯市場有效性的匯率理論等為代表的新近發展起來的匯率理論。技術分析經歷了參數到非參數，線性到非線性的發展過程，其中，參數方法主要包括隨機游走模型、自回歸移動平均模型、自回歸條件異方差模型、自我激勵閥值自回歸模型、指數平滑過渡自回歸模型等。非參數方法主要包括小波分析、遺傳算法、人工神經網絡等。

近年來，非參數方法中的神經網絡技術的出現，極大地提高了匯率預測中的樣本擬合度。其中，按誤差逆傳播算法訓練的多層前饋網絡——BP 神經網絡，更加能夠直接生動地反映系統的動態特性，因此它更適合對具有非線性的、動態的特征的匯率系統進行預測。

二、實證研究

理論上，一個三層的神經網絡就能夠以任意的精度逼近連續函數，也就能滿足實證建模的需要。盡管歐元等其他主要貨幣的比重也在逐漸上升，但是中國的儲備貨幣目前仍然是以美元為主，因此，若是能夠對人民幣兌美元匯率進行準確地預測，貨幣當局就能更好的把握人民幣和主要儲備貨幣之間復雜的變動關系，進而靈活地、有針對性地對儲備貨幣的結構進行調整，從而做好外匯風險的防范工作。在本文中，將采用單步預測法對人民幣兌美元中間價進行預測，這不僅有助于我國匯率政策、利率政策等的制定和調整，也有助于企業進行科學的國際貿易決策。

（一）數據選擇

本文實證研究將選擇2010 年01 月04 日起至2012 年10 月25 日為止央行公布的每日人民幣兌美元匯率中間價，一共680 個數據為樣本，進行實證研究 (所有數據均來源于中國人民銀行網站：http://www.pbc.gov.cn/)。 之所以取2010 年至2012 年近700 個數據，原因如下：

一方面，人民幣兌美元匯率是一組時間序列數據，對于它的預測工作，當然是時間上越近的數據越有代表性，預測結果更有說服力；

另一方面，Kang 在利用神經網絡對時間序列進行預測的研究中就指出了，要想模型有較好的預測能力并不一定必須要具備很大的數據樣本。再后來，Walczak 以不同規模的數據樣本，利用神經網絡模型對匯率序列進行預測后，通過比較結果，得出在多數情況下兩年的數據樣本就足以使神經網絡模型產生合適的預測精度這一結論。

（二）構造訓練樣本

把前679 天的數據按順序輸入，作為網絡的一個輸入數據（即把樣本數據從第1 個取到第679 個，作為p），然后將后面的679個數據輸入，作為網絡輸出即目標數據（即從第2 個取到第680 個，作為t），按這個方式進行滾動式的排列，就形成了神經網絡的訓練樣本。

（三）選用三層結構的BP 神經網絡建立預測模型

理論上，一個三層的神經網絡就能夠以任意的精度逼近連續函數。由于其具有操作性強、計算量小等優點，目前仍是多層式網絡訓練的首選網絡結構之一，并且已經被人們推廣應用于各種各樣實際問題的解決中。因此，我將在本論文中采用三層網絡建立模型進行匯率預測。

輸入層和輸出層的節點數主要由輸入變量決定，這些將直接影響網絡的學習效果和泛化能力。對時間序列預測問題，輸入層節點數等于所開窗口大小，在本例中輸入層節點數即為679，加之本文只限于一維時間序列，所以預測值只需要用一個輸出層節點來表示，本例中輸出層節點數為1。隱藏神經元主要應用于學習數據的內部規律，試湊法是確定最佳隱藏層節點數的一個常用方法，即先用較少的隱層節點數進行訓練，然后逐漸增加隱藏層節點數，用同一樣本集進行訓練，從上述訓練結果中選出網絡誤差最小的一組確定為隱藏層節點數。在用試湊法的時候，也可以用一些經驗公式來確定隱藏層節點數。用這些公式計算出來的隱層節點數的粗略估計值，可以作為確定隱層神經元數目初始值的大致參考。

即隱藏層節點數為28—37 中的一個整數。

在MATLAB 中進行訓練，得到訓練結果如下，見表1：

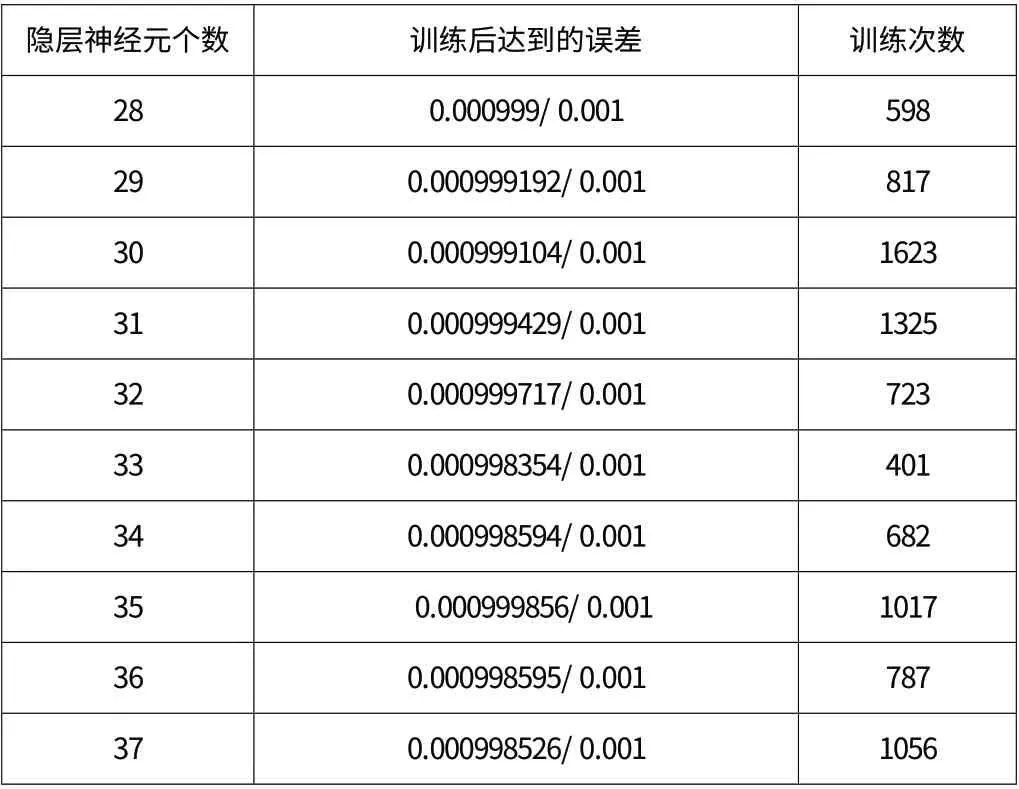
表1 訓練結果

網絡誤差最小所對應的隱層神經元個數為28，因此，本例中b即為28。

（四）預測過程的具體實現

建立一個新的前向神經網絡，%設置網絡隱單元的神經元數、輸出層節點數及訓練函數net=newff(minmax(p)，[28，1]，{‘tansig’，’purelin’}，’traingdm’)；% 當 前 輸 入層 權 值 和 閾 值inputWeights=net.IW{1，1}，inputbias=net.b{1}；%當前網絡層權值和閾值layerWeights=net.LW{2，1}，layerbias=net.b{2}；%設置訓練參數net.trainParam.show=50，%每50 步顯示一次誤差，net.trainParam.lr=0.05，%訓練步長，net.trainParam.mc=0.9，%Sigmoid 參 數0.9，net.trainParam.epochs=10000，% 最大訓練次數，net.trainParam.goal=1e-3，%設定的期望誤差，一般為0.001；%調用TRAINSCG 算法訓練BP 網絡[net，tr]=train(net，p，t); % 對BP 網絡 進行仿真p_TEST=6.3047，A=sim(net，p_TEST)；% 計算 仿 真 誤 差E=t -A，MSE=mse(E)。

按上述過程在MATLAB 中進行操作后，得到誤差趨勢圖如圖1 所示：

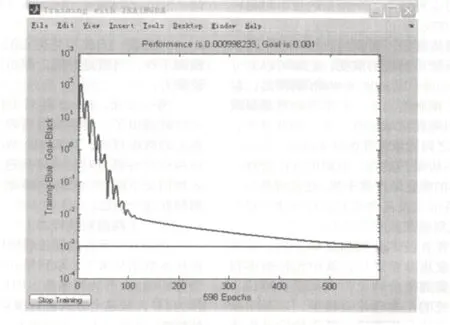
圖1 BP 神經網絡訓練誤差趨勢圖

當前輸入層權值和閾值、當前網絡層權值和閾值部分結果（因版面問題未能全部列示）如表2 所示：

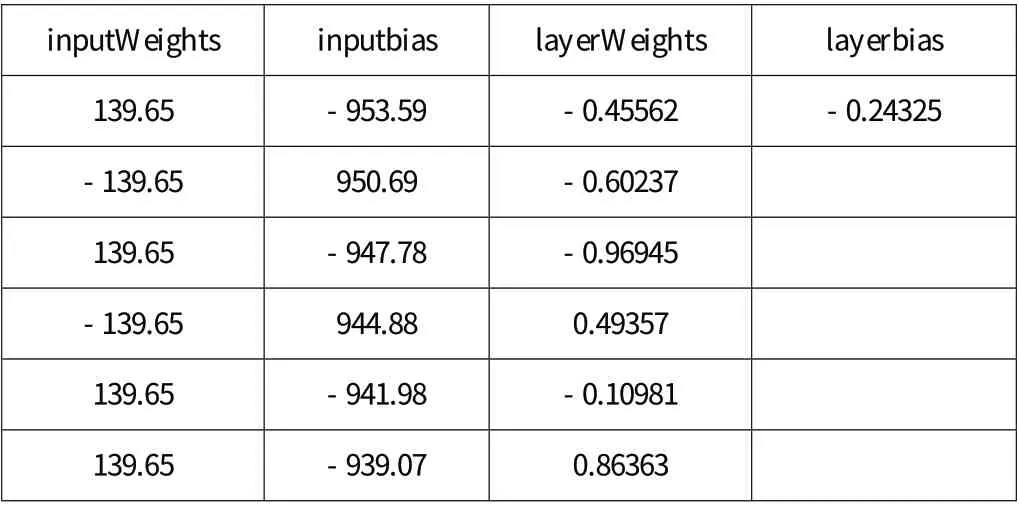
表2 輸入層權值和閾值、當前網絡層權值和閾值部分結果

預測值A 為6.3251，MSE=0.00099823.

2012 年10 月26 日人民幣兌美元匯率中間價為6.3010，與預測值相差0.0241，誤差率為0.38%，明顯地，預測值與實際值相差并不是很大，說明用MATLAB 進行BP 神經網絡預測模型進行匯率預測效果不錯，具有可行性。

經過上述的探索操作，我們根據2010 年01 月04 日起至2012 年10 月25 日為止中國人民銀行公布的每日人民幣兌美元匯率中間價，共680 個數據樣本預測出了下一日的匯率中間價，預測過程合理規范，并最終達到了實證目的。進一步地，還可以通過滾動預測法預測以后更多的匯率，操作思想同上，不再贅述。

盡管BP 神經網絡對匯率預測效果不錯，但還是存在一些不足之處。神經網絡模型只利用了匯率的歷史數據來進行預測，并沒有考慮影響匯率變動的經濟、政治等因素，也沒有將其量化入模型中，故只能在外部環境較為穩定的前提下進行短期預測。此外，BP 神經網絡本身也在算法上存在一些缺陷，比如它的收斂速度較慢慢、容易導致局部最小、訓練結果不穩定等。

[1]丁輝，基于神經網絡模型的人民幣匯率預測研究，2008.

[2]王莎.BP 神經網絡在股票預測中的應用研究，2008.4.

[3]趙振勇.基于遺傳BP 神經網絡的股市預測，2007.5.

[4]孟生旺.神經網絡模型與車險索賠頻率預測.統計研究，2012(03):22-26.

[5] http://www.pbc.gov.cn/中國人民銀行