三體船操縱特性仿真研究

姚迪, 鄒艷忠, 李光磊

(1. 海軍駐大連426廠軍事代表室，大連 116000；2. 海軍92956部隊三中隊，旅順 116041；3. 海軍駐九江地區軍事代表室，九江 332007）

0 引言

近年來國內外對三體船的研究業已廣泛的展開，唯獨對于三體船的操縱性研究甚少[1]。然而操縱性作為重要的航海性能與戰技指標，迫切需要開展對三體船操縱性的研究，該方向的研究具有十分重要的學術理論意義與工程應用價值。鑒于此，本文以典型三體船為目標船型，研究了三體船水動力導數計算方法，進而對三體船的操縱特性進行了系統的計算機仿真，并對仿真計算結果進行了廣泛的分析與研究。

1 三體船操縱運動數學模型的建立與分析

研究三體船操縱性，首先要選定合適的操縱運動數學模型，本文選擇MMG分離模型作為三體船操縱運動基本數學模型[2]。

1.1 船舶操縱運動方程

通過坐標變換并進行近似處理，就可以得到艦船操縱性運動線性化方程，如下式所示：

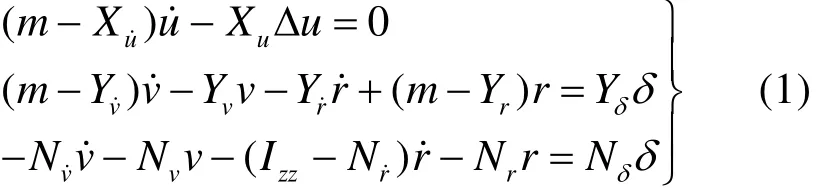
1.1.1 船舶操縱線性相應方程

在工程實用中，往往更關注首向角φ及其角速度r隨時間變化的規律。對于一般的船舶，由于操舵速度是有限的，且船舶本身慣性很大，對舵的響應基本是一種緩慢運動，在操舵不是很頻繁的情況下，由線性化的水動力模型可以導出關于r的一階方程：

式中：

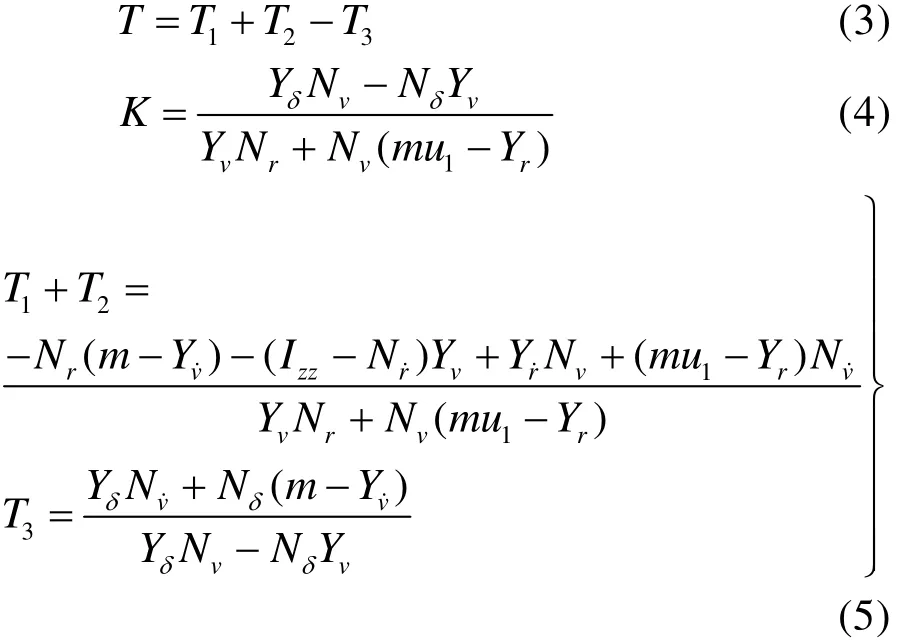
方程式(2)即為野本兼作的一階線性KT響應方程[3],也稱為野本方程。

1.1.2 船舶操縱非線性相應方程

船舶二階線性響應模型為

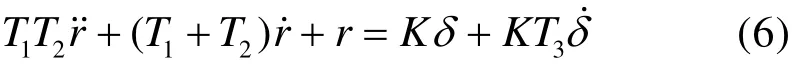
二次方程可以在“線性平均”的意義上用于描述中等幅度的操縱運動。這時上述方程中隱含的流體力導數不再是ν，r為零時的流體動力曲線的斜率，而是采用運動狀態為ν和r時有關動力曲線的斜率。因此在非線性情況下，各種線性流體動力導數將依賴于r的變化，系數K、T1T2、(T1+T2)和KT3由各種線性流體動力導數組成，即：

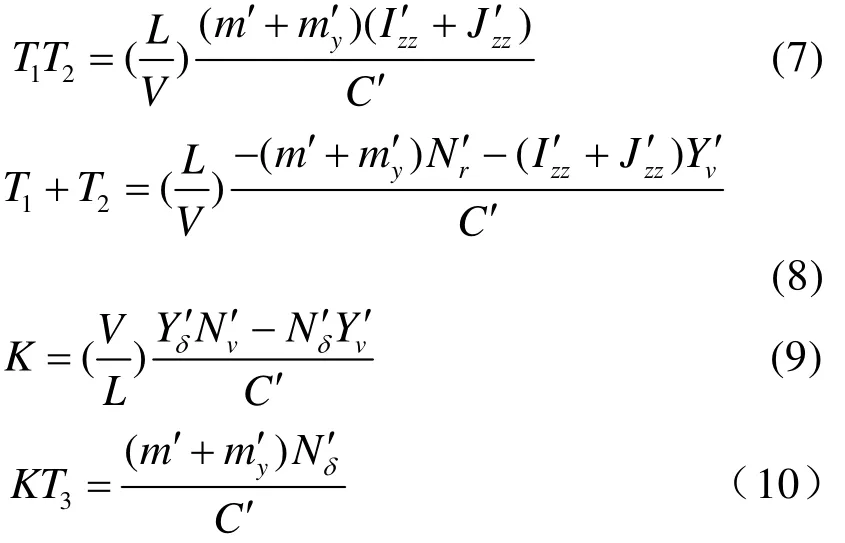
類似于線性化一階KT響應方程，式(6)對于一階系統也近似有效，即

1.2 計算機仿真模型

直接從水面船舶平面操縱運動基本微分方程式(1)出發，求出作用于船體上的力后，進一步求解時域微分方程就可以實現對船舶操縱性運動進行計算機仿真，求得船舶操縱運動的動態特性，以及船舶運動的軌跡和航向的時域特性。由于本文是研究三體船操縱運動的動態特性的計算機仿真，所以舵是通過估算設計出的，未對三體船舵的設計問題進行深入研究。采用龍格—庫塔法求解三體船操縱運動的動態特性的計算機仿真微分方程，在不考慮船舶的橫搖與縱搖對船舶影響的情況下三體船操縱特性預報和操縱運動的動態特性的計算機仿真方程組如下：

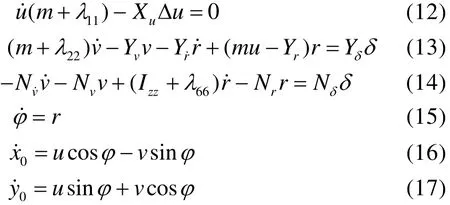
聯立求解式(12)-式(17)即可以求出各種舵角下的艦船運動軌跡。

2 水動力導數計算

船舶操縱性各數學模型中的系數是水動力導數或其組合值，所以各水動力導數確定(本文指計算確定)是船舶操縱性研究和操縱運動計算機仿真的重要環節。就目前的發展水平來言，水動力導數的計算方法有回歸公式法，勢流理論方法以及粘性流體CFD方法[4]等。勢流理論方法以及粘性流體 CFD方法又細分為計入波面影響和不計波面影響(靜水面假設)兩種階次的。由于回歸公式法和不計波面影響的勢流理論方法對求解水動力導數的數學物理模型計算簡便，且對計算結果精度影響不大，本文選擇上述兩類方法作為三體船操縱性研究和仿真中水動力導數計算方法。

2.1 水動力導數數值計算分析

三體船操縱性水動力導數計算中要沿用單體船水動力導數估算方法并加以修正，此時面臨著對所謂“三體問題”進行處理。本文處理三體問題的方法如下：1）采用三片體分離模型(即 MMG模型)的總體思路處理三體問題；2）由于坐標系原點取在主船體水線面中點(1/2船長處)，故在側體力矩類水動力導數計算中需進行坐標變換(即力矩的移軸定理應用)；3）片體間水動力干擾問題的分析處理。

通過運用切片理論[5，6]、細長體理論[7]和三維面元法，并結合“三體問題”的處理原則，對各水動力導數進行求解。對三體船而言，上述三維面元法的優點是可將三個片體視作整體一并解出其繞流速度勢，這樣得出的結果自然包含了片體間的水動力干擾作用，而經驗公式方法、切片法、細長體理論等計算方法在求解三體船水動力中是不具有這一優點的。

2.2 實例計算

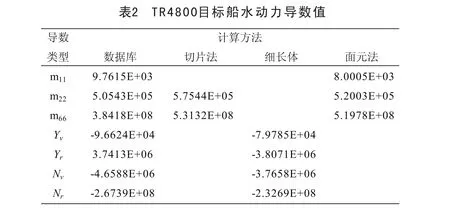
本文對目標船進行操縱運動計算機仿真，其主尺度參數和仿真結果見表1和表2。

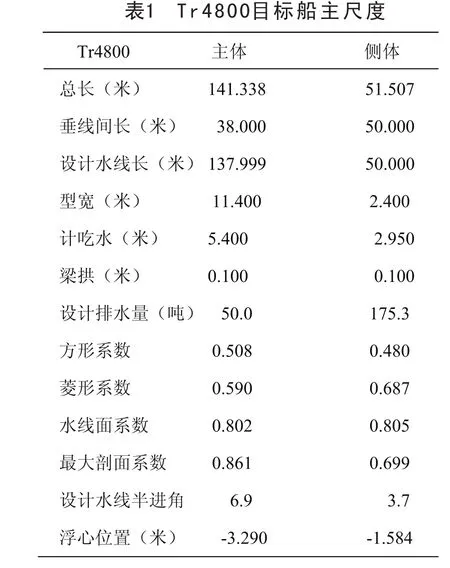
按照三體船操縱運動數學模型，對三體目標船型操縱運動進行計算機仿真，繪出相應的仿真計算結果圖形。

3 三體目標船操縱運動仿真

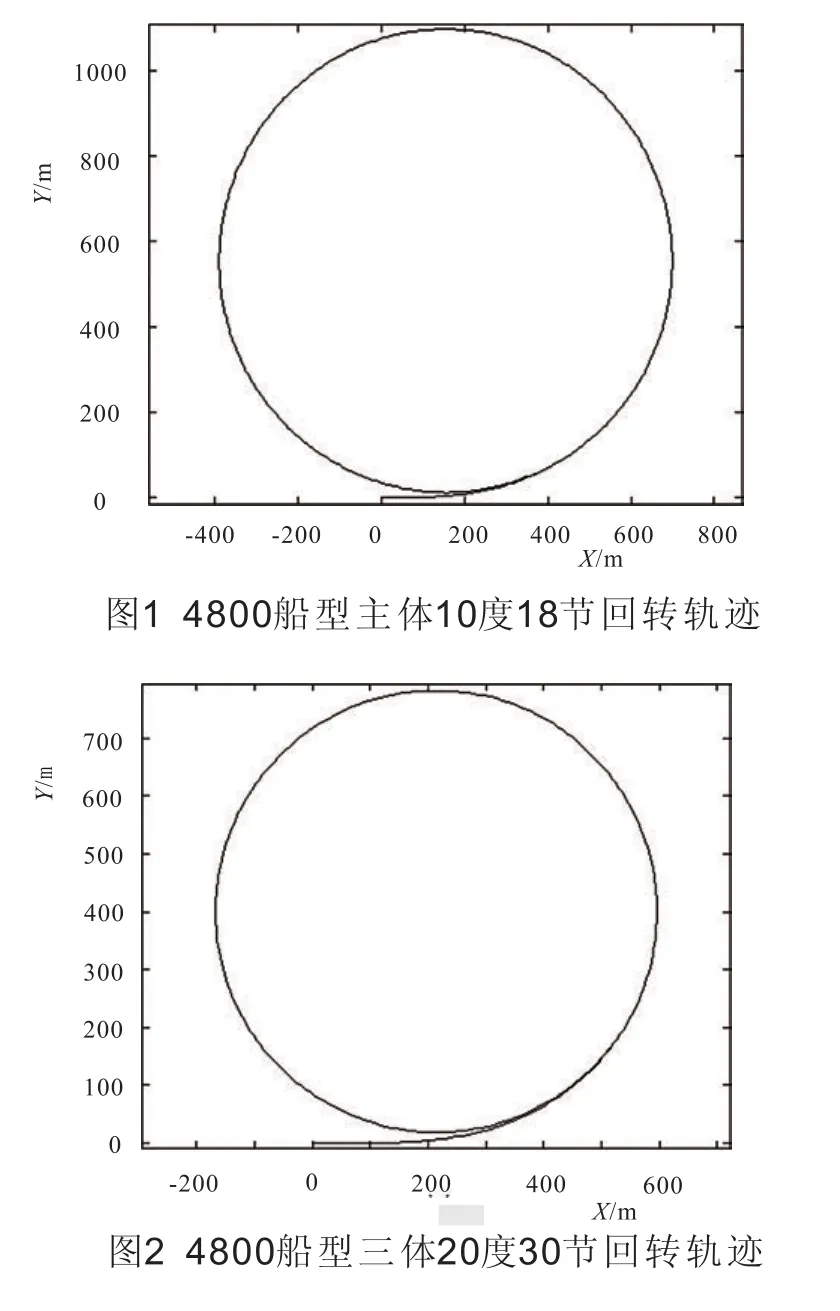
3.1 三體船回轉軌跡仿真

在不同舵角與不同航速下對目標船型回轉過程中的運動軌跡進行計算機仿真，計算結果如圖1、圖2所示。

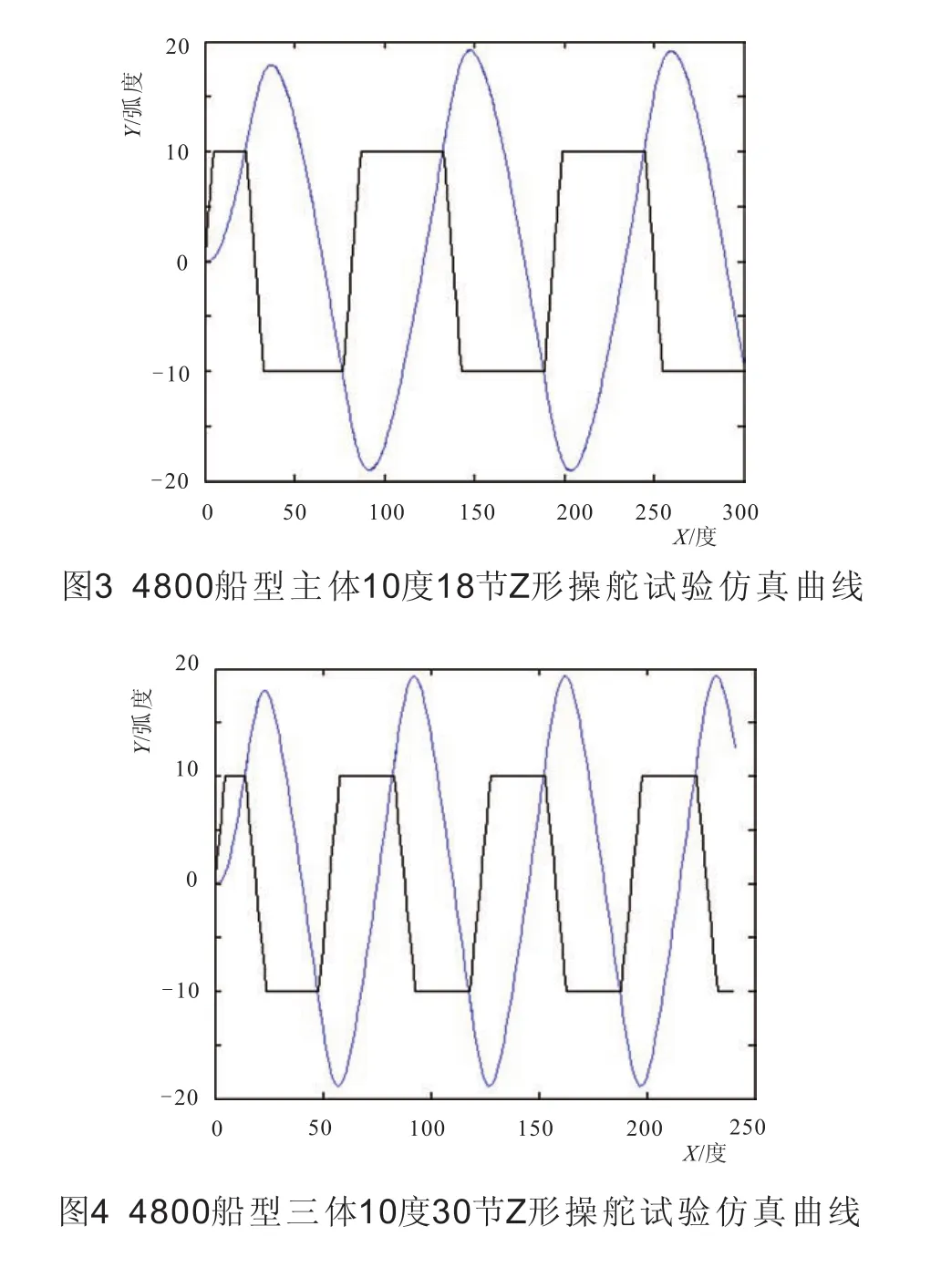
3.2 三體船Z形試驗軌跡仿真

在不同航速下對目標船型進行Z形試驗的運動軌跡進行仿真，計算結果如圖3、圖4所示。

4 結語

本文圍繞三體船的操縱性展開研究，在選取適用于三體船操縱運動仿真的數學模型的基礎上，對目標船型的操縱性水動力導數進行計算，根據計算得到的水動力導數按本文所采用的船舶運動方程對三體船回轉運動軌跡、Z形操舵試驗曲線等進行了計算機數值模擬和仿真，得出了典型的操縱運動數值仿真計算曲線，為三體船研發積累了技術資料，提供了技術支撐。

：

[1]盧曉平，酈云，董祖舜.高速三體船研究進展[J].海軍工程大學學報，2005, (2)：43-48.

[2]吳秀恒，劉祖源，施生達.船舶操縱性[M].北京：國防工業出版社，2005.

[3]盛振邦，劉應中.船舶原理[M].上海：上海交通大學出版社，2004.

[4]王燕飛，朱軍，張振山.評估水動力系數對潛艇操縱性影響的一種方法[J].船舶力學， 2005，9(5)：61-68.

[5]West R E，Hime W G.Chloride profiles in salty concrete [J].Material Performance，1985，24(7)：29-36.

[6]馬山，宋競正，段文洋.二維半理論和切片法的數值比較研究[J].船舶力學，2004，8(1)：35-43.