硼氫化鈉水解制氫系統噪聲特性研究

李大鵬

（海軍工程大學，武漢 430033）

0 前言

隱蔽性是潛艇最為重要的戰術性能。電化學發電機AIP潛艇使用NaBH4水解制氫要涉及到復雜的兩相流動現象，在含有氫氣-蒸汽氣泡的NaBH4溶液兩相流動以及氣泡生長、浮升、融合、脫離等過程中，會有噪聲產生，有必要研究其噪聲特性，為降低兩相流動噪聲提供理論依據。

1 乳狀液中的壓力波傳輸

制氫器反應區內的兩相混合物從結構上可分類為氣體乳狀液，其特征為含有氣體、氣泡尺寸分布離散上。氣體成分包括水解過程中產生的H2、水蒸氣、乙硼烷（B2H6）等，但 B2H6等氣體在H2中含量不超過0.05%，可忽略對氣泡水動力學特性的影響。使用確定蒸汽-氣泡相間換熱的導熱積分方程解析解，對于有限幅度擾動，Δ p/ p ＜ 1，可將壓力擾動方程組寫成（1）、（2）式。

其中， ao=[kpo/(ρo?o)]1/2-相間轉換滯止音速；β=/(6? )-氣泡脈動與慣性效應有關的離散系數； m =3kpoρlcpl（dT / d p ）s/(ρgnr)-常數；v-無相變混合物氣泡有效粘度； al-液體導溫系數；?-體積含氣率； r-相變潛熱。

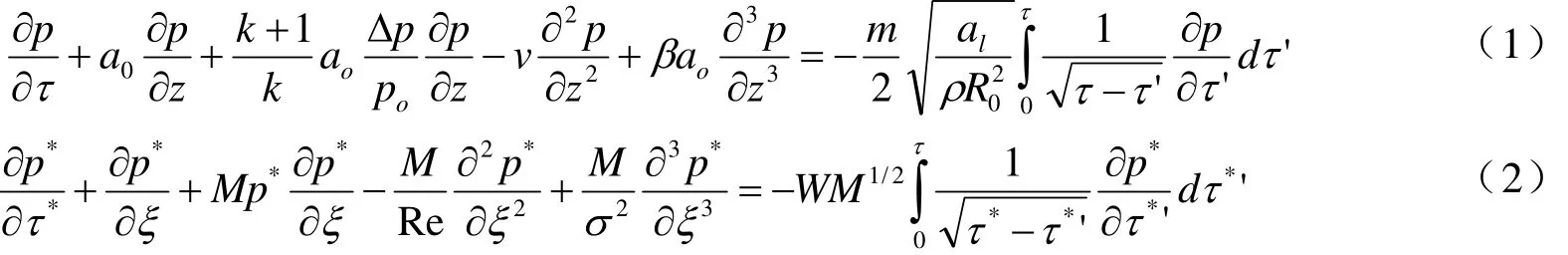
寫成無因次形式，使用初始參數 Δp0為幅值，h0為長度，a0為特征速度。對于有限波長擾動，使用評價準則：1）σ=h0[(k + 1)Δp0/(2kp0β)]1/2， 定 義與 彌 散 效 應 相比，非線性效應波動截面的待求變量；2）W=m{kp0alh0/[2 πa0Δp0(k +1)]}1/2，表征相間換熱和非線性效應的相對強弱；3）Re =(k+ 1)a0Δp0h0/(2kp0v)，表征無相變介質中耗散。對于沖擊波類型擾動，使用定義相變和波的非線性擴張影響。當 W*或W較大時，狀態具有相變特征，且當W→0時，波傳播取決于非線性和慣性效應。與參數W有關，氣泡介質中可能存在波束、單沖擊波或振蕩等多種結構[2]；4）M= uo/ao= (k +1)Δ po/(2kpo)，馬赫數。H2管道上自動閥門突然關閉引起壓力擾動按水力沖擊處理[3]，有，其中中音速；ρ-H2密度； w0-到達閥門處的H2速度。

假設壓力擾動沖擊到達制氫器中蒸汽-氣體乳狀液邊緣表面時沒有發生變化。在氣泡介質中，混合波結構由準則數 W*確定。 W*≥1的區域稱為“熱狀態”區域，該區域內有限波長壓力波混合時相間換熱占主要影響。 W*＜0.1的區域稱為“慣性狀態”區域，該區域內有限波長壓力波演變特征主要取決于準則數σ。其他準則數還包括僅由初始擾動形式定義的準則數σ*。當σ*>σ，氣泡中為波束；當σ*<σ，氣泡中為長波。沖擊波可能是二重薄壁結構，呈單調（M<0.3）或振蕩（M>0.3）變化。

ho≈ 4 Ro/為計算參數 W*和W，取使用參數：2.5 MPa壓力下， R0=56，?o=0.28，擾動參數 Δp0=0.014 MPa，得到 h0=0.0056 m，W*=5.74 μm，即 W*＞1，所以擾動處于“熱狀態”區域。當 W*≥1時，氣泡形成過程中的非線性和慣性效應不明顯，將波的演變方程寫成線性形式

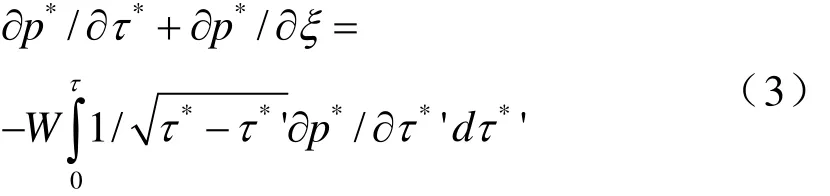
對上式進行拉普拉斯變換，得到不同初始擾動下方程解。對于階躍式初始擾動，有。利用概率積分函數和誤差函數，將上式寫成

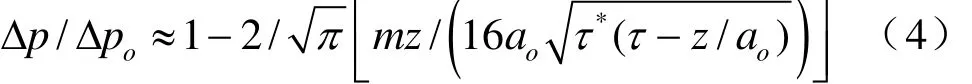
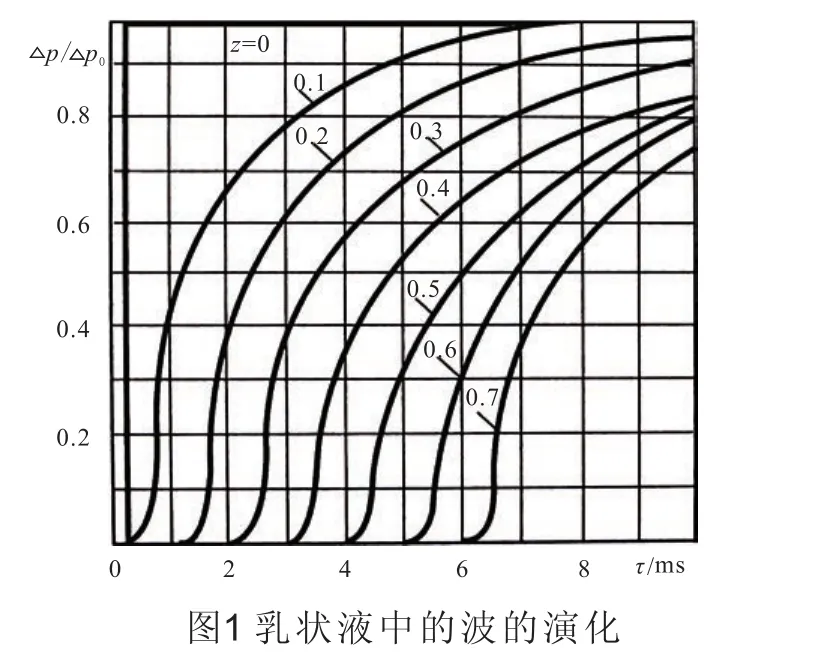
根據上面公式計算得到蒸汽-氣體乳狀液中波的演變過程見圖 1。由圖可見，波運動前沿被拉長。盡管0.7 m距離處波幅值減小，但所有幅值在經10 ms后都超過了初始幅值的80%。在“熱狀態”區域，蒸汽-氣體乳狀液中都不存在有沖擊波和帶有陡峭前沿的有限寬度區域，但幅值足夠大，能夠引起管道中流動振蕩。另外，H2管道上閥門開啟或關閉引起擾動也會造成兩相流動波動。

2 氣泡生長過程中的噪聲

彈性介質中機械應力或局部壓力發生改變的任何過程都可能產生聲波。制氫器反應區中蒸汽-H2氣泡的形成和生長將伴隨有聲能輻射。液相中壓力波動頻率和幅度取決于氣泡生長速度。蒸汽-H2氣泡生長緩慢。當汽、液相存在密度差時，氣泡生長可能在液相中形成壓力波。當汽、液相具有相同密度時，在氣泡生長過程的任何時刻，系統處于平衡狀態，氣泡內部壓力由液體靜止壓力和拉普拉斯方程確定的表面張力決定。汽、液相間密度差使得初始時刻由于存在質量交換，氣泡中壓力急劇增大，然后根據液體被排擠程度，壓力開始下降并趨向于穩定，液體中因此出現慣性形成的過余壓力。由于不均勻性增大，汽相中汽泡將發生波動，并在液相中產生正和負的壓力波。

實際蒸汽相氣泡生長不呈單調變化。列氣泡壓力方程時假設氣泡壓力變化為氣泡生長和波動造成壓力變化之和。如將蒸汽相氣泡體積波動用諧波形式表示，氣泡中過余壓力變化寫成

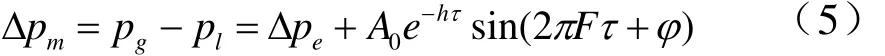
其中pg-氣泡中蒸汽相壓力； pl-液相靜止壓力；Δpe-液體慣性形成的氣泡過余壓力；Ao-壓力波動的初始幅值；h-波動衰減系數；F-波動頻率；?-波動的初始相。

壓力波動初始幅值應與氣泡核心中蒸汽相壓力Ao成正比，由臨界半徑表達式 Rc=2σ vo/Δ?，得到 Ao= 2 kAσ /Rcr=kAvo/Δ?，其中 kA為無因次比例系數，根據經驗數據，kA= 2.0× 10-5ρl/ρg。氣泡開始波動時，實際上液相中壓力波動經過第一個周期后就開始衰減。經過一個循環后波動幅值減小，取 m =20，則衰減量 h =F ln(m/ n)= 3.0F，其中 n 為壓力波動的循環數， n=1。

將上面相應表達式帶入氣泡過余壓力變化表達式，得到

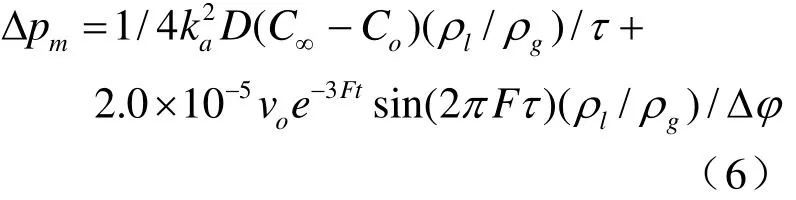
當氣泡直徑以指數規律增大到一定程度，等號右側第二項可忽略。實際上氣泡體積波動頻率一般為幾千Hz，可使用下式定義氣泡自由波動頻率[8]： Fo=（3k p∞/ρl）0.5/(2πRo)，其中 R0-氣泡平均直徑； p∞-對應氣泡直徑R0的液相靜止壓力；k-氣體絕熱指數。在制氫器反應區所處狀態下，氣泡直徑255 μm，氣泡自由波動頻率61.8 kHz，由于粘性和質量交換的存在，實際值比計算值低。當液體中壓力頻率處于常見分布區間時，氣泡生長產生壓力pc=D( C∞- Co)ρl/(4ρgτ)。

假設所有 N個氣泡都位于制氫器反應區內并作為等強度聲源，則作用在制氫器殼體壁面上的聲波強度

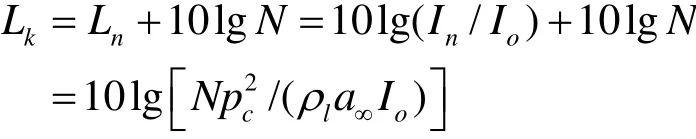
其中 Lk-作用在制氫器殼體總聲波強度，db； Ln-氣泡聲波強度，db；In-單個氣泡的聲波強度，db；pc-氣泡生長產生壓力表達式定義的聲壓，Pa；a∞-液體中聲波傳播速度，m/s；Io-液體中聲波強度 極 限 值 ， 為 2.66× 10-16W/m2， 氣 體 中 為1.0× 10-12W/m2。將氣泡生長產生壓力表達式代入，得到

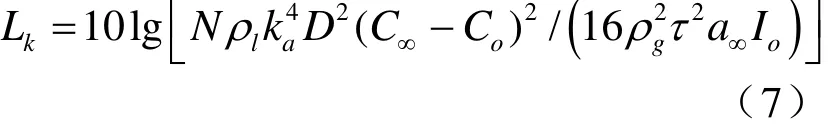
計算 Lk時使用了如下假設：蒸汽-氣體乳狀液中聲波強力發散，且主要在氣相體積中傳播。其他參數取值： N=140000， ρl=1070 kg/m3，ka=1.5，C∞=100 kg/m3， D= 5× 10-9m/s，ρg=2.8kg/m3，τ=1 s，a∞=1500 m/s。帶入計算，得到作用在制氫器殼體上聲波強度僅為30 db。使用傅里葉積分變換確定水動力學噪聲的幅頻譜。導出上式時如下假設：所有氣泡以同樣幅值同步增大。實際上，制氫器反應區的某些位置上氣泡增大情形要復雜些，此時液體中聲壓將是時間的非周期函數。聲壓譜密度可通過反向傅里葉積分關系式確定：

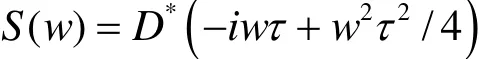
若已知聲壓譜密度，使用直接傅里葉變換并整理，得到

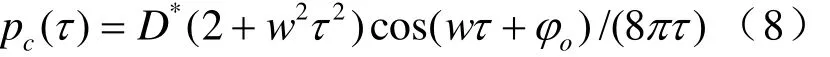
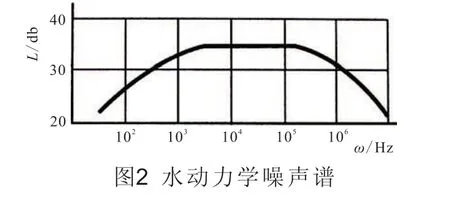
帶入聲波強度表達式，得到100～106Hz頻率范圍內作用在制氫器殼體上的總聲波強度。計算得到的制氫器反應區中蒸汽-氫氣氣泡生長過程的水動力學噪聲譜見圖 2。可見，在 3～102kHz這一較寬頻率區間內，曲線較為平坦，聲波強度實際上保持不變。作用在制氫器殼體上的聲波強度不大，約 35 db。這樣的高頻聲波強度對于保證制氫器具有較高的聲學性能是完全可以接受的。

3 氣泡融合時的聲能輻射特性

制氫器反應區內，蒸汽-氣體氣泡以不同速度浮升，期間會出現氣泡融合，形成更大體積氣泡，氣泡的部分能量會轉化為聲能。

假設兩個半徑均為 R1的氣泡融合，融合過程中，氣泡中蒸汽-氣體溫度未發生改變，融合為等溫過程。新氣泡形成的主要條件是初始氣泡與新形成氣泡中的氣體質量相等。使用克拉拍龍和拉普拉斯方程，可以得到新氣泡半徑:

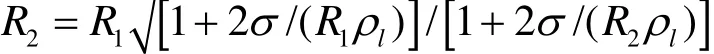
當 2 σ/(R1ρl)≈2σ /(R2ρl)＜＜1時 ， 有R2≈ 1.26R1。融合時釋放出能量：

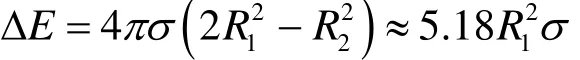
如果氣泡融合發生在距離液面的一定位置處，則伴隨融合還進行球狀聲波的變形過程。兩個氣泡融合時釋放出的部分能量轉變成聲能，即

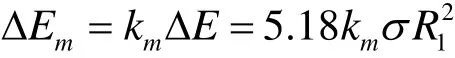
km為聲波能量轉換系數。聲功率

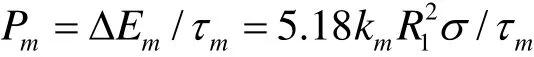
其中，τm-氣泡融合時間。使用萊利公式得到τ =0.915R （ρ / p∞）0.5。假設氣泡融合時間為生成半徑為R2氣泡所需時間，得到 τm=0.68 R （ρl/p∞）0.5。帶入聲功率表達式，得到

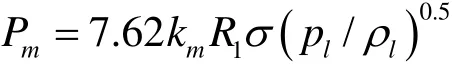
氣泡融合時的輻射聲能為氣泡總勢能的30%左右[6]。使用關系式 En/Es= Rp∞/(3σ)確定球狀氣泡勢能與其表面能之比，兩個氣泡融合時的能量轉換系 數 km=0.9σ /(R p∞)， 帶 入 上 式 ， 得 到。由于氣泡融合是在液、氣相分界面上進行，空氣中距離聲源 r處的聲波強度I=Pm/(4π r2)。聲波強度水平LB=10 lg I/I0，其中Io=10-12W/m2。 距 離 制 氫 器 1 m處 ， 當pl= 2.5× 106Pa，計算得到聲波強度為44 db。計算時水表面張力σ=0.05 N/m。實際上，制氫器反應區溶液中含有較強的表面活化劑 NaOH，會減小表面張力，并相應降低聲波強度。

氣泡融合強度不僅取決于表面活化劑，還與氣泡尺寸有關。相鄰氣泡間距越大，融合所需接近距離就越小。乳狀液中，可用融合速度不變的二階反應方程描述:，其中No-初始時刻單位體積乳狀液中氣泡數目；Nτ-至τ時刻氣泡融合數目。

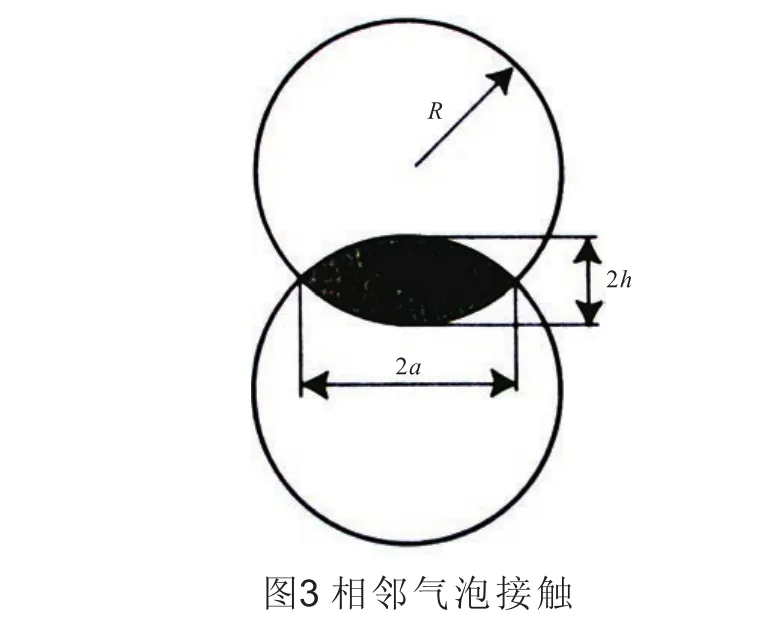
估算相互吸引靠近的兩個氣泡的聲波強度時，假設接觸位置處沒有作為吸附層的分隔氣泡存在，且氣泡一直保持球狀，氣泡球心距離2 h，該距離與氣泡球心間的初始距離 2 R相比可以忽略。見圖3。由幾何關系可知， R2= a2+ (R -h)2，且 h << R ，有 a2=2Rh。由于氣泡接近，氣泡表面能減小了 Δ Eσ=- 4πRhσ，相鄰氣泡間表面張力Fσ=-ΔEσ/h =-4πRh 。氣泡間張力相當大。當R=250 μm，Fσ=1.57×10-4N，而作用在浮升氣泡上擠出力 FAr=(4/3)πR3ρlg=6.87×10-7N，表面張力大大超過擠出力。氣泡融合具有隨機性，融合氣泡數目及相應聲脈沖數目須使用統計方法估算。假設1 s時間內，氣泡融合數目服從正交對數分布規律，聲脈沖平均數目可用下式估算：，其中 N-聲脈沖最小數目，N=1；-聲脈沖最大數目，等于氣泡總數目一半，≈ 18000，得到聲脈沖平均數目在130左右。距離制氫器 1 m處噪聲強度LB,Σ= Ln,1+ 10lgmin=65。可見，氣泡融合時的噪聲強度比氣泡生長形成時大得多。

氣泡融合時可將聲壓作為過程參數的函數。對聲脈沖壓力進行傅里葉變化并整理，得到聲能譜密度:

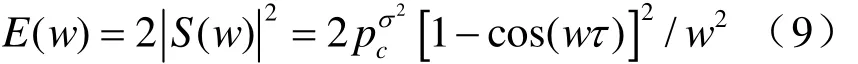
4 氣泡脫離時的聲能輻射特性

如氣泡脫離時 30%能量轉變為聲能

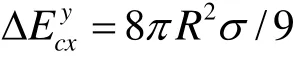
聲功率

距離聲源r處的聲波強度

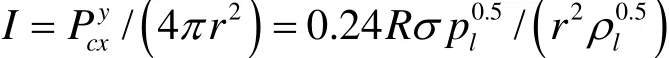
在 r =1 m距離處聲波強度 L= 10lg(I/Io)=82 db。制氫器噪聲中最大的組成是液相表面的氣泡脫離噪聲。能輻射損失表達式未考慮與氣泡脫離時形成液滴及液滴上升到一定高度等有關的能量損失，故計算值略高。但該式作為定性估算時是可信的。表面活化劑會降低溶液表面張力，會降低噪聲水平。

對流體設備中空泡效應造成的空氣噪聲測量表明，僅有 0.01%左右的空化氣泡功率會轉化成聲能。考慮聲能耗散，氣泡脫離液面造成聲波強度

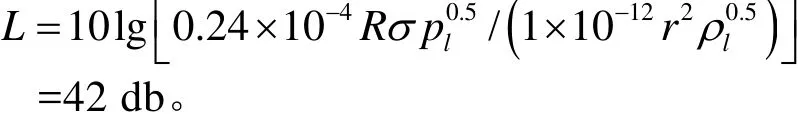
設自液面脫離的氣泡半徑均為 250 μm，有Ny個聲脈沖源，氣泡在0.2 m高度反應單元內的催化劑表面上生長。由氣泡脫離直徑表達式，計算得到的催化劑表面氣泡脫離半徑為 50μm。由氣泡半徑隨時間變化表達式計算，氣化核心產生并增大到50 μm半徑氣泡需時0.1 s，相鄰氣泡浮升1 mm。0.2 m高度反應單元內有200個氣泡層，每個氣泡層有190個左右氣泡，液相上部躍離出液面的氣泡數目 Ny=190，此時制氫器內氣泡脫離液面造成的噪聲強度= L + 10lg Ny= 42 +10lg190=65 db。氣泡融合與氣泡脫離產生的噪聲強度相等。如果認為氣泡聲強度頻率在200 kHz左右。

5 結束語

制氫過程涉及到氣泡的形成和生長、浮升、運動等兩相流動現象，制氫器內乳狀液中壓力波傳輸特性、氣泡生長過程中噪聲、氣泡融合和脫離時聲能輻射特性、聲波傳輸速度的計算可基于已有的兩相流動模型進行，并在此基礎上，有針對性地從運行參數選擇、制氫器設計等方面實施降噪。

：

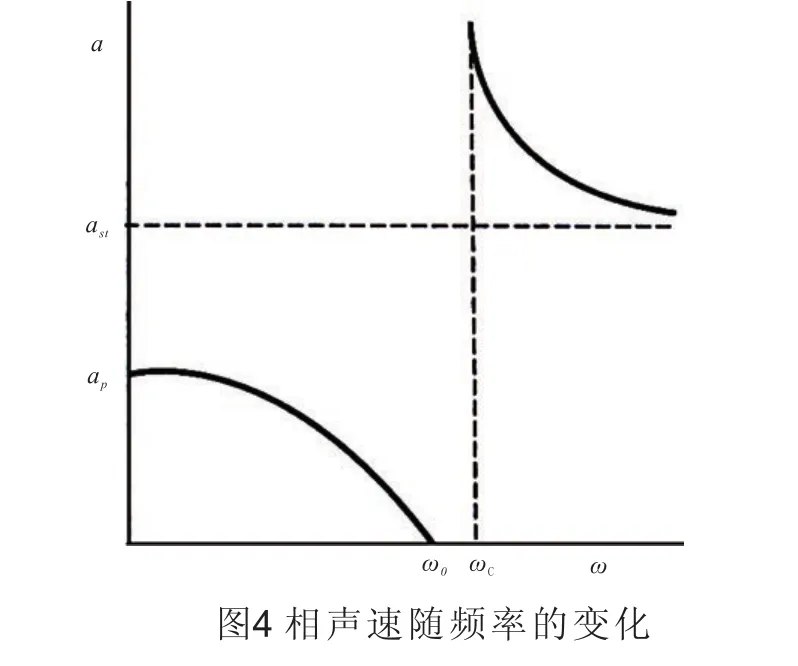
[1]Nakorakov V.E., Schreiber I.R. Model of disturbances in the steam-fluid mixture[J]. TVT, 1979, 17 (4):798-803.

[2]Kutatelas S.S., Nakorakov V.E. Heat and mass transfer and wave in steam and fluid system[M]. Novosibirsk:Science, 1984.

[3]Sterenliht D. Hydrodynamics[M]. Moscow:Energoatomizdat, 1991.

[4]Nakorakov V.E., Pokusaev B.G., Schreiber I.R. Wave dynamics of gas and steam-fluid system environments[M]. Moscow: Energoatomizdat, 1990.

[5]Deadic A.N., Zamukov V.V., Deadic V.A. Ship air-independent power plants[M]. St. Petersburg:Shipbuilding, 2006.

[6]Miniovic I.R., Pernik A.D., Petrovsky V.S.Hydrodynamic sound sources[M]. Leningrad:Shipbuilding, 1972.