3D建模在制圖課第一角畫法與第三角畫法對比學習中的應用

吳家福

（貴陽學院 機械工程學院，貴州 貴陽550005）

0 前言（第一角畫法與第三角畫法介紹）

世界各國在繪制機械圖樣時，機件的圖形均按正投影方法繪制，但投影法則分別采用第一角或第三角畫法。ISO 國際標準規(guī)定：在表達機件結構中，第一角畫法和第三角畫法同等有效。第一角畫法起于法國，盛 行于歐洲大陸、德、法、俄等國，其中美、日及荷蘭等國原先亦采用第一角畫法，后來改采用第三角畫法至今。隨著中國制造的國際化，國際間技術交流和國際貿易的日益增長，為更好地學習發(fā)達國家的先進技術，要求在日常工作中也會閱讀和繪制第三角畫法圖樣[1-2]。因此，大學制圖課中很有必要對第一角畫法與第三角畫法進行對比學習，從而促進制圖知識鞏固，增強識圖、繪圖能力[3]。

利用三個互相垂直的平面將空間分為八個分角，分別稱為第Ⅰ角、第Ⅱ角、第Ⅲ角……第Ⅷ角，如圖1 所示。

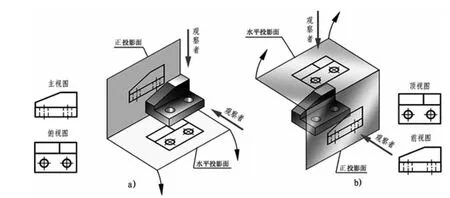
凡將物體置於第一象限內，以「視點(觀察者)」→「物體」→「投影面」關系而投影視圖的畫法，即稱為第一角法。亦稱第一象限法。第一角法展開后之視圖排列如下，以常用之三視圖(前視、俯視、右側視圖)而言，其右側視圖位於前視圖之左側，俯視固則位於前視圖之正下方，如圖2（a）。

凡將物體置於第三象限內，以「視點(觀察者)」→「投影面」→「物體」關系而投影視圖的畫法，即稱為第三角法。亦稱第三象限法。第三角法展開后之六個視固排列如下，以常用之三視圖而言，其右側視圖位於前視圖之右側，而俯視圖則位於前視圖之正上方。如圖2（b） 。

這里將兩種畫法的投影規(guī)律總結如下：（1）兩種畫法都保持“長對正，高平齊，寬相等”的投影規(guī)律；（2）兩種畫法的方位關系是：“上下、左右”的方位關系判斷方法一樣，比較簡單，容易判斷。不同的是“前后”的方位關系判斷，第一角畫法，以“主視圖”為準，除后視圖以外的其它基本視圖，遠離主視圖的一方為機件的前方，反之為機件的后方，簡稱“遠離主視是前方”；第三角畫法，以“前視圖”為準，除后視圖以外的其它基本視圖，遠離前視圖的一方為機件的后方，反之為機件的前方，簡稱“遠離主視是后方”。可見兩種畫法的前后方位關系剛好相反；（3）根據前面兩條規(guī)律，可得出兩種畫法的相互轉化規(guī)律：主視圖（或前視圖）不動，將主視圖（或前視圖）周圍上和下、左和右的視圖對調位置（包括后視圖），即可將一種畫法轉化成（或稱翻譯成）另一種畫法。

1 建立對比學習資料庫

建立對比學習資料庫是第一角畫法與第三角畫法學習中重要內容，利用3D 建模建立起一定數量零件的三維立體庫，并分別用兩種方法從立體到平面實現(xiàn)三視圖庫，最后通過連線選擇的方法增強應用，使學習的效果得到進一步提高。

1.1 建立三維立體庫

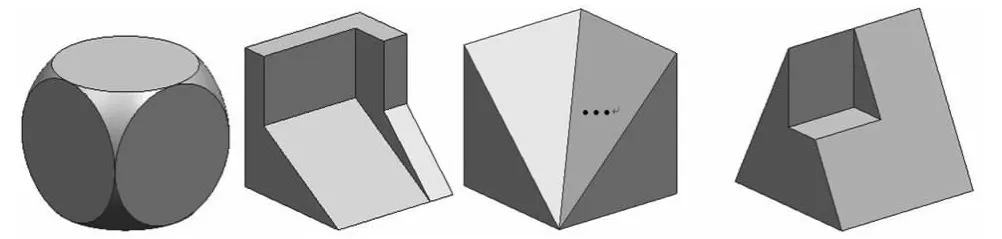
以機械制圖教材、機械制圖習題集上出現(xiàn)的機件為基礎，同時收集企業(yè)訓練中出現(xiàn)的題目，選擇UG、ProE 或Solidworks 等三維軟件中一種對所收集的機件繪制三維立體圖，保存為通過格式，如Igs 或Step等格式備用。過程如圖3 所示。

1.2 根據三維立體庫零件分別創(chuàng)建第一角和第三角平面三視圖庫

三維立體庫建立起來后，針對立體機件，還要對其進行兩次三維到平面的操作，首先，是把三維立體庫中所有零件的第一角畫法平面三視圖用AutoCAD 或CAXA 電子圖板等軟件繪制出來，并保存為第一角平面三視圖庫。其次，把三維立體庫中所有零件的第三角畫法平面三視圖用AutoCAD 或CAXA 電子圖板等軟件繪制出來，并保存為第三角平面三視圖庫。也可以直接用三維軟件中三維變立體功能把三維立體庫中的立體分別轉化出第一角平面圖和第三角平面圖，過程如圖4 所示。

2 利用連線配對法增強兩種畫法實際應用能力

三維立體庫和兩種畫法的三視圖庫建立起來后，可以采用用配對法使學生在平面和三維之間建立聯(lián)系，分別從三維立體庫、三視圖庫隨機抽取10 個機件為一組，請學生進行連線，從而增強學生對兩種畫法的實際應用能力，如圖5 所示。

3 掌握3D 軟件應用，從平面到立體鞏固對比學習成果

學生基本掌握空間想像能力后，從第一角畫法和第三角畫法的投影關系思考，就能認知視圖投影，區(qū)分二者之間的差別，能在兩種投影圖中自由切換識圖。此時可以提出進一步的學習要求，讓學生掌握一門3D 軟件的操作應用，看懂平面圖后，通過軟件來親自動手繪制更多的機件三維立體圖，使對第一角平面圖和第三角平面圖的知識轉化為應用能力，使知識沉淀在個人能力中，成為不會輕易丟失的個人知識構成要素。

4 結論

3D 模型直觀，在觀察過程中可以根據旋轉、剖切，對于正投影下的第一角和第三角都能很好的再現(xiàn)其觀察結果[4]，對于視圖思維、空間想象能力的培養(yǎng)是十分有益的，學生通過一定數量的模型的學習，能自由在立體到第一角平面圖和第三角平面圖進行想象，也可以在第一角平面圖和第三角平面圖到三維立體中逆向思維，給予了學生空間想象思維實現(xiàn)的物質依據，如果能進一步升華到掌握3D 軟件建模，那么會更好地把知識變成能力，凝固為個人知識體系的一部分。

［1］劉小年.機械制圖[M].北京：高等教育出版社,2007.

［2］中華人民共和國國家標準局.技術制圖與機械制圖[M].北京：中國標準出版社,1996.

［3］毛文武.美國加州大學圣迭哥分校工程圖學課程教學研究[J].工程圖學報,2007(5)：172-177.

［4］RAISOR Max E.Engineering Graphics Principles with Geometric Dimensioning and Tolerancing[M].Mission KS：SDC,2002.