基于UG的斜齒輪造型設計

王洪珍

(徐州機電工程高等職業學校，江蘇 徐州221011)

機械傳動中，漸開線斜齒輪的應用相當廣泛。由于齒廓曲線比較復雜，尤其是齒根部分的過渡曲線與齒輪的加工方式有關，所形成的過渡曲線也不一樣。為了得到齒廓曲線，必須通過數學模型來描述齒廓的各段曲線。

1 齒廓曲線的數學表達

斜齒輪端面齒廓曲線包括漸開線、齒根過渡曲線、齒根圓弧和齒頂圓弧。

1.1 齒廓漸開線的數學表達

斜齒輪端面漸開線的生成方法與直齒圓柱齒輪基本相同。不同之處在于斜齒輪法面模數mn、 法面 分度圓壓力角α、 法面齒頂高系數h*an和法面頂隙端系數c*an為標準值，而齒廓曲線方程中用到的是端面壓力角αt與端面模數mt。

建立圓的漸開線參數方程：

式中：rb為基圓的半徑；θ 為發生線與基圓的接觸點A 與B 之間所對應的圓心角。

1.2 齒廓過渡曲線的數學表達

過渡曲線與齒輪加工方式有關，但其原理基本相同。標準齒條刀具頂部比普通齒條多出一段c*m，用于被加工齒輪的齒根部分切出齒頂間隙。

現以齒條形刀具參數為例進行分析，刀具齒廓的頂部有兩個圓角，Cp是圓角的圓心，圓角半徑等于rp。刀具各參數間具有以下關系：

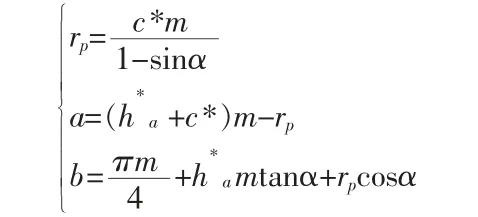
式中：m 為齒條的模數；a 為點Cp至中線的距離；b 為點Cp至齒形中心線的距離；α 為齒條的壓力角也就是被加工齒輪的分度圓壓力角；h*a為齒頂高系數；c* 為頂隙系數；rp為圓角半徑。

被加工齒輪齒廓的漸開線部分由刀具的斜直線部分切出，而齒根過渡曲線則由刀具的圓角部分切出。如圖2 所示，加工過程中刀具的加工節線與齒輪的節圓相切純滾，刀具圓角的圓心將形成延伸漸開線，因此齒輪的過渡曲線是該延伸漸開線的等距曲線。P 點是節點，nn 是刀具圓角與過渡曲線接觸點的公法線，可求得延伸漸開線等距曲線，即齒根過渡曲線的參數方程為：齒根過渡曲線的參數方程為：

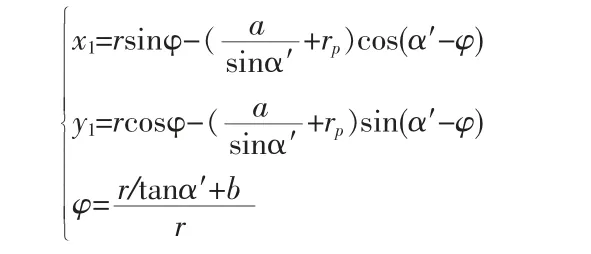
式中：α' 為公法線與刀具加工節線間的夾角；r 為齒輪分度圓半徑；φ 為角度參變量。

由于刀具的圓角部分和與其連接的兩段直線相切，所以當刀具圓角與齒根過渡曲線剛開始接觸時，M 垂直于刀具的齒側直線，此時nn 與嚙合線重合，α' 等于齒條與齒輪的分度圓壓力角α； 當齒條齒輪轉動到α'＝π/2 時，齒條形刀具的頂部直線段與齒根過渡曲線末端接觸，然后由該段直線切出齒根圓弧。由此可知，α'∈[α，π/2]。

1.3 齒槽曲線段間的連接

實現齒輪參數化建模，必須用表達式將齒槽各段曲線精確描述且曲線連接不能有歧義。

1.3.1 漸開線

由于要求與過渡曲線極大值點及給定的一半徑略大于齒頂圓半徑的圓弧相接。結合漸開線的性質：

θF＝tanαF－αF，根據圖2 所示的原理，假設B 點為過渡曲線極大值點，并且假設K 點為與漸開線相接的略大于齒頂圓半徑的點。最終可以確定漸開線的取值范圍：θ∈[tanαB，tanαK]。曲線1 是直接由式（1）繪出的漸開線，曲線旋轉θ1后得到曲線2。根據對稱性可列出另一半漸開線的方程，得到曲線2 關于X 軸對稱的漸開線：

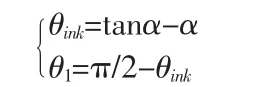
1.3.2 過渡曲線

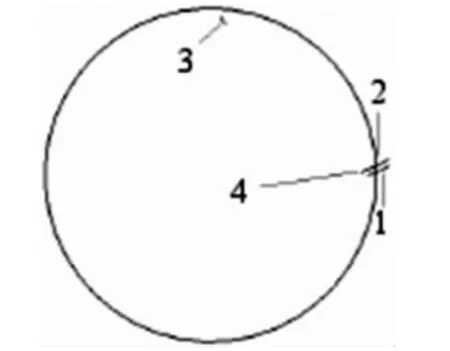
如圖3 所示，曲線3 直接由式（3）繪出。曲線旋轉θ2后得曲線4。利用對稱性可列出關于X 軸對稱的另一段過渡曲線的方程，并繪出其曲線。根據過渡曲線的取值范圍可以得到極大值點B（xmax,ymax）與極小值點A（xmin,ymin）。由極值點可確定：

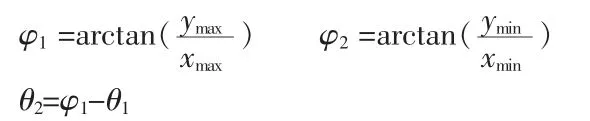
1.3.3 齒根圓弧

如圖3 所示,通過曲線3 的極小值點A（xmin,ymin）與X 軸的夾角φ2，以及曲線3 變換到曲線4 所旋轉的角度θ2，可以確定齒根圓弧的取值范圍：

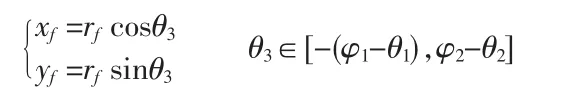
2 造型設計

2.1 造型設計步驟

漸開線斜齒輪造型設計的關鍵是齒輪（包括齒廓）相關參數的建立，在UG 中設計過程如下：

（1）利用表達式建立相互關聯的表達式；

（2）使用基本曲線功能中的規律曲線選項，通過方程式，并利用已經建立的表達式繪制出漸開線曲線、過渡曲線、齒根圓弧、略大于齒頂圓弧，從而形成首尾相接的單個齒槽線串；

（3）生成與螺旋角相關聯的螺旋線；

（4）進入草圖，以齒根圓弧的圓心畫出齒頂圓，一定要用表達式來定義齒頂圓的直徑；

（5）利用相關的特征操作（拉伸、沿引導線掃描、沿圓周陣列）完成漸開線齒輪的三維建模。

初始化齒輪如圖4 所示。

2.2 表達式的生成

對圓柱斜齒輪而言，其端面是漸開線，符合齒廓嚙合基本定律，即可改變齒數z、法面模數mn、壓力角α、螺旋角β 等常用參數，可以得到不同的圓柱斜齒輪的三維模型。建立表達式可以用以下兩種方式：①選擇Tools＞Expressions，直接輸入表達式。②建立一個文件名稱用英文字母或數字表示的純文本文檔，并輸入相關的表達式，保存并關閉后更改文件擴展名為.exp； 然后在UG 中選Tools＞Expressions＞Import，輸

入建立.exp 文件。

在建立對基本參數賦初值的表達式時采用第一種方式，所建立表達式如下：

Z=25 //齒數

mn=4 //法面模數

alpha=20 //法面壓力角

beta=12 / /螺旋角

ha=l ∥法面齒頂高系數

c=0.25 //法面頂隙系數

h=20 //齒輪厚度

2.3 實現

斜齒輪的造型實現要求齒輪能夠實現在其設計要求發生改變時，它的結構尺寸也相應地改變以滿足新的設計需要。為此，只需要將上述所建立的齒輪實體模型的相關特征參數進行更改，就可以生成各種相關參數的齒輪三維模型。

3 結論

運用UG 進行齒輪精確建模時，齒廓曲線的數學表達十分重要。借助UG 中的規律曲線功能可以直接生成齒廓曲線，無需對其進行修剪、變換，對齒廓曲線實現了完全參數化設計。由于采用了UG 內部表達式工具，避免了編程處理，通用性比較強。齒輪精確造型設計對齒輪的應力分析、干涉檢驗、數控仿真等都有實際意義。

［1］孫桓，陳作模，葛文杰.機械原理[M].北京：高等教育出版社，2006.

［2］白劍鋒，賀靠團，黃永玲，侯寶義.UG 在漸開線斜齒輪參數化設計中的應用[J].機械設計與制造，2006（7）：71－73.

［3］江洪，酈祥林，李春表，等.UG5.0 典型實例解析[M].北京：機械工業出版社，2007.