淺析積分的分部積分法及其人文教育價值
周 均
(長江師范學院 數學與計算機學院,中國 重慶408100)
0 引言
不定積分的計算是微積分教學的重點和難點,讓學生掌握不定積分的計算方法,由于分部積分法具有復雜性和靈活性,因此讓學生更透徹地掌握這種方法的實質、思路,形成解題策略,對提高學生的觀察問題、分析問題的能力極其重要。筆者在近幾年的教學中,對分部積分法的規律作了一些比較簡單的總結,形成本文。
1 方法的分析
無論分部積分法有多么復雜和靈活,通過分析發現也有其獨特的規律,即從大的方面來說,分部積分法的中心問題是解決兩類函數的乘積的積分,其基本的思路是把一個積分分為兩個部分(函數)的積分,其一是由V′求V,這是一個理論意義上的積分(無積分符號),其二是我們面對積分的關鍵是如何確定′確定的標準是前面提到的兩個積分容易求得,即把求積分轉化為求易求的積分根據這一要求很容易觀察出被積函數的形式(或結構),根據觀察在教學中將分部積分法用較簡潔的語言概括為“三多選多”、“指多選多”、“代反選反”、“代對選對”、“指弦任選” 等五種方法。
1.1 “三多選多”,“指多選多”
這里的“三”指三角函數的正余弦,“指”指指數函數,“多”指的是多項式函數,即正整指數冪函數,“三多選多”、“指多選多”指正余弦、指數函數與多項式在一起的積分選多項式函數為U(以后指的“選”就是指選擇為U),正余弦、指數函數為V′的計算方法。如應用一次分部積分法選擇為 V′時,由求 V 就比較簡單,同時在使用分部積分法后的積分多項式的次數降低了一次,這樣反復應用同一選擇方法的分部積分法,最后,使多項式降低為零次,使積分變為只有一類函數積分顯然積分簡單容易了。
解:根據上面的分析原積分
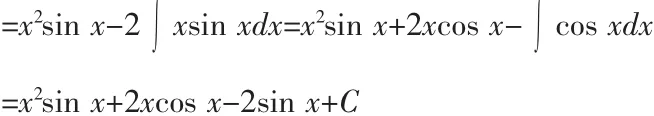
類似地,“指多選多”有如下例子
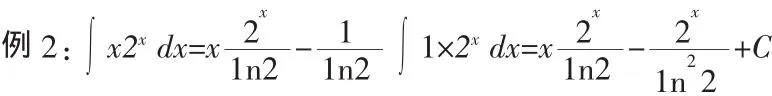
1.2 “代對選對”, “代反選反”
這里的“代”指代數函數(如冪函數、根式函數、有理函數),“對”對數函數的簡稱,“反”指反三角函數。即代數函數與對數函數、反三角函數之積的積分,選擇對數函數、反三角函數為U,因為使用一次分部積分法后,對數函數、反三角函數的導數為代數函數,即積分 ∫U′Vdx只為一類函數(代數函數)的積分如:這個積分是有理函數積分,顯然易于計算。
1.3 “指弦任選”
“指”同1.2是指數函數的簡稱。這兩個函數都是超越函數,其導數和積分都不會改變函數的類型,因此使用分部積分法時可以任選其中其一為U,兩次使用分部積分循環后計算得到結果。如:
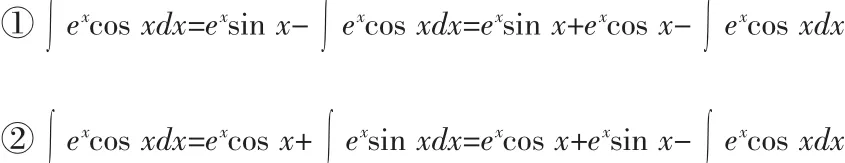
顯然①中兩次使用分部積分法時都選的U=ex,②中兩次使用分部積分法時都選的U為正、余弦,即指弦任選都能殊途同歸,使積分回到積分這里值得注意的是兩次使用分部積分法及兩次選擇的U都必須是同一類函數,否則如下:
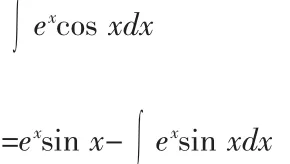

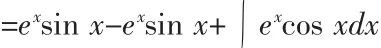
第一次選擇U=ex,第二次選擇U=sin x,會產生循環計算,不能求出積分(事實上,前面的四種積分多次使用分部積分法時也應用注意這一點)。
2 人文價值和認知心理學價值分析
通過以上分析,不難發現,一方面,我們用如詩歌一般的語句對每一種具體方法進行了歸納表述,使得方法簡潔明了,并將各語句賦予了特定的涵義,將深抽象的數學思想和方法用簡潔的語言進行了表征,而且進行了分類,只要學生理解其涵義后,形成有意義的知識組塊,既有利于知識的理解,又有利于方法的掌握。這既是符合認知心理學的有意義學習,又是數學教學中的人文價值之所在,同時還容易形成認知心理學所倡導的解題策略。另一方面,通過對照前面1.1與1.2發現,好象這兩組方法選擇U的方法好象相反,似乎是相矛盾的,同時又統一于整體的分部積分法之中,從分部積分法的總的思路中可看出有潛在的積分V′求V,同時有導數如這樣將不能求的積分轉化為易求的積分,這正與《周易》的“相生相克,宏微顯生”“易,窮則變,變則通,通則久”等觀點有異曲同工之妙。事實上,在高等數學的教學中有很多地方就有數學文化或數學人文精神,要對學生進行數學文化或數學人文精神的教育關鍵是在數學教師如何深刻理解數學文化,如何充分挖掘教材的潛力,創造性地進行數學人文教育。
[1]陳傳璋,等.數學分析[M].北京:高等教育出版社,1983,7.
[2]四川大學數學系高等數學教研室.高等數學[M].北京:高等教育出版社,1994,4.
[3]文衛星,等.數學人文精神之我見[J].數學教學,2002(4).
[4]張奠寅.中學教材中的“數學文化”內容舉例[J]數學教學,2002(4).
[5]張慶林.當代認知心理學在教學中的應用[M].重慶:西南師范大學出版社,1995,12.
[6]張慶林.高效率教學[M].北京:人民教育出版社,2002,3.
[7]鄭萬耕,等.周易與現代文化[M].中國廣播電視出版社,1997,8.

