一種差動輪式競賽機器人的路徑跟蹤方法

賀洪江，鐘志賢

(1. 河北工程大學 裝備制造學院，邯鄲 056038；2.河北工程大學 信息與電氣工程學院，邯鄲 056038)

0 引言

隨著機械設備自動化程度的提高，移動機器人的應用領域也越來越廣泛。競賽機器人也作為機器人學的一個重要分支，對其的跟蹤控制也得到了廣泛的研究。在差動輪式自主移動競賽機器人路徑控制中，主控制器通過連續采集編碼器脈沖，記錄機器人走過的真實里程。要對路徑進行跟蹤控制還需要機器人的實時角度，可以使用陀螺儀測得，但是由于陀螺儀成本高，易受環境影響[1]。針對上述問題，本文介紹一種只基于兩個對稱安裝的編碼器作為傳感器的閉環路徑控制方法，為以后多傳感器信息融合進行路徑規劃提供物理實現的保證。

1 編碼器安裝和系統組成

兩輪差動驅動的移動機器人的底盤結構示意圖如圖1(a)所示，左右兩輪由兩個電機驅動，前輪是一個可以自由轉動的角輪。兩編碼器軸上裝上輪子，做成隨動碼盤輪,對稱地安裝在底盤上，并有彈簧機構使其在隨動過程中接地良好不被懸空。

在機器人的路徑控制中，對直流電機轉速和位置的控制有較高的要求，有高精度的電機控制，才可以知道自己的位置和跟蹤自己要行走的路線。所以系統采用專用電機控制盒對電機進行轉速控制。控制系統的組成如圖1(b)所示。

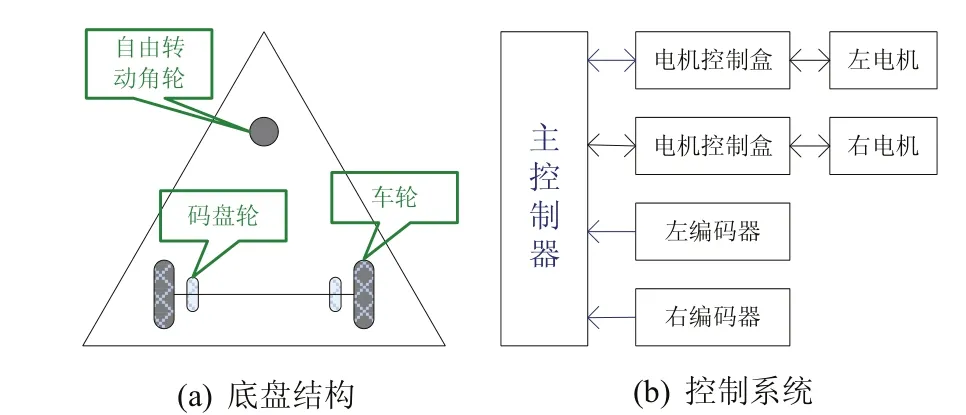
圖1 系統結構

2 編碼器采集距離和角度

2.1 實時距離換算

機器人運動過程中編碼器A、B線輸出波形如圖2所示。

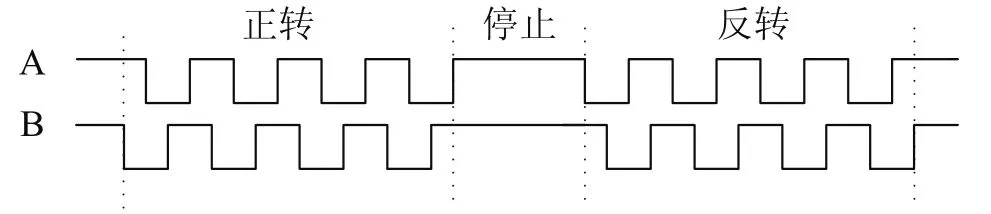
圖2 編碼器輸出波形

1）單邊沿采集方法：把A線接到主控制器外部中斷，下降沿觸發，在中斷服務程序中判斷B線，若B線為低電平則正轉，脈沖計數加加，若B線為高電平則反轉，脈沖計數減減[2]。

2）雙邊沿采集方法：同樣把A線接到主控制器的外部中斷，雙邊沿觸發，在中斷服務程序中先判斷B線，若B線為高，再判讀A，若A也為高則表示正轉，脈沖計數加加，若此時A為低則表示反轉，脈沖計數減減。若進中斷后先判讀的B線為低，則返回。

實際應用中，有時機器人在看似靜止的情況下，由于機器人的微動編碼器輸出的波形會在某一邊沿來回跳變，此時若采用單邊沿采集則會造成脈沖計數的錯誤遞增或遞減，而雙邊沿采集方法可以相抵消，避免機器人停止時，卻有里程值改變的問題。

編碼器采集到的脈沖數與里程成正比例關系。因此，可以由脈沖數轉化為里程值。分別對左右兩個編碼器進行標定，即找到脈沖數與里程值的比例系數。采用多次測量取平均的方法減小誤差。實驗中機器人5次行走2m測得的脈沖數如表1所示。

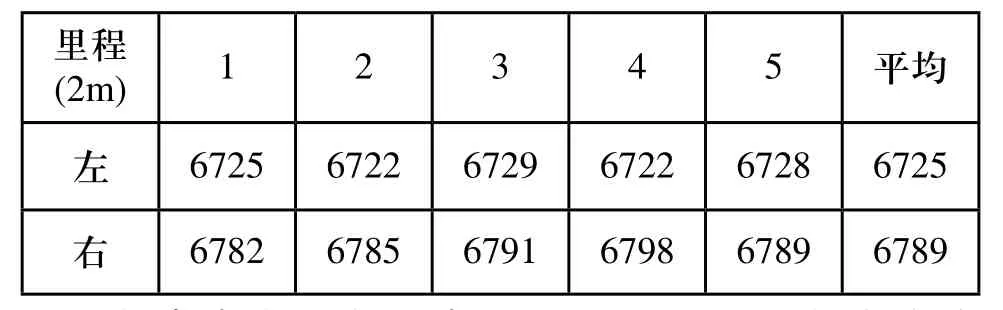
表1 左右碼盤標定實驗數據

程序中左里程值表示為：Dis_L = 左脈沖數× 2000 / 6725 (mm)；

程序中右里程值表示為：Dis_R = 右脈沖數× 2000 / 6789(mm)；

車體的總里程為左右里程的平均值，表示為：Dis_M=( Dis_L+ Dis_R)/2。

2.2 實時角度換算

由于是對稱安裝，左右兩車輪的運動軌跡可以用左右兩碼盤輪的運動軌跡來等效。根據左右兩個碼盤采集的里程值，在保證兩碼盤不離地的情況下，根據弧長公式計算出車體轉過的實時角度，方法如圖3如示。

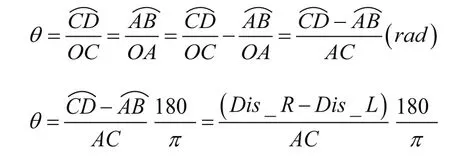
其中，Dis_R為此時機器人右碼盤記錄的里程，Dis_L為此時機器人左碼盤記錄的里程。

具體應用時標定車體的初始朝向為0，則向左轉過的角度為正值，向右轉過的角度值為負值。

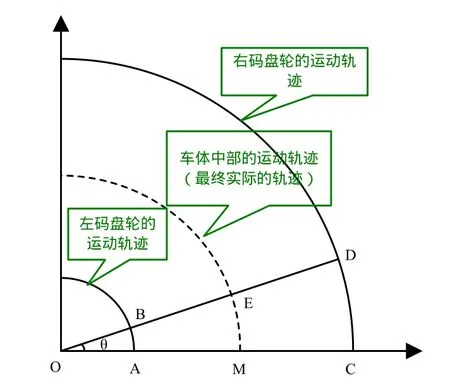
圖3 角度換算示意圖

3 直線、弧線跟蹤控制

3.1 直線跟蹤

控制中所用的到距離和角度均來自雙編碼器的計算。在程序中采用經典PID控制，主控制器根據隨動編碼器得到的信息進行PID計算，結果輸出給電機控制盒控制電機。理想情況下，若機器人嚴格進行直線運動則左右兩個編碼器采集的里程值之差因該為0或者為某一常量，所以把兩編碼器采集的里程之差作為跟蹤控制的量，0或某一常量作為設定值，進行PID控制。但是實際對于直線行走的PID校正，誤差的形式有兩種：角度誤差θ和中心位置誤差d。

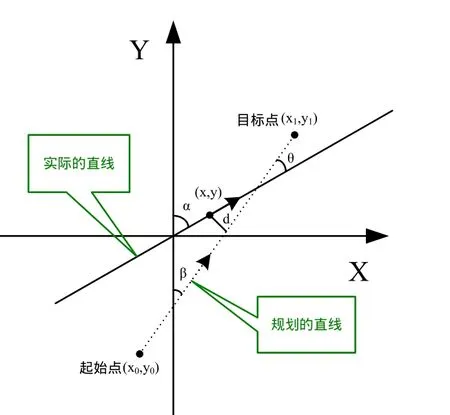
圖4 直線跟蹤示意圖

如圖4所示，直線行走時機器人的當前朝向角為α，β為規劃好的直線在坐標系中的角度，由平面幾何可得下式：

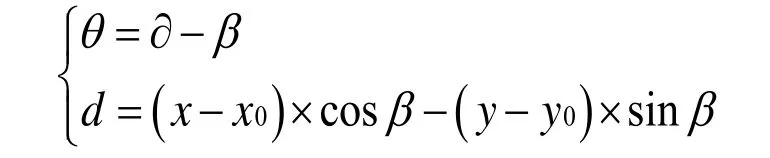
θ和d這兩個誤差相對獨立，可以分別進行檢測控制，這里為了減少PID參數整定，通過加權將他們合成一個誤差e，只用一套PID參數進行校正，即把e作為檢測值，0作為設定值。如下所示：e=d+kθ。

加權系數k反映了機器人角度誤差與位置誤差相漲或者相消的程度，實際上它還包含了一定的微分的意義[3]。

對于綜合后的總誤差e，我們采用增量式PID算法對其進行校正,在程序中具體實現的函數名為：

INT32S PID_common(INT32S set, INT32S feedback, PID_Uint *p);

其中，入口參數分別為，設定值(set)，檢測值(feedback)，和指向PID參數結構體(PID_Uint)的指針。

根據開環實際測試，可以估算得出角度偏差和位置偏差的加權系數為3，在實際調試時也驗證了這個權值是合適的。在實際應用時還需給出，起始點坐標和目標點坐標，加減速距離，起始速度，最高速度和末速度，然后根據增量式PID校正算法，對機器人的左右輪速度進行實時地校正。實現沿規劃好的直線行走。

3.2 弧線跟蹤

類似直線的跟蹤思想，算法的參考目標是轉彎半徑R和機器人相對初始朝向的實時轉彎角度θ，在這兩個參照量和實際測得的機器人狀態的偏差之間做加權求出總誤差e，減少參數個數，以方便參數的調試。跟蹤示意圖如圖5所示。

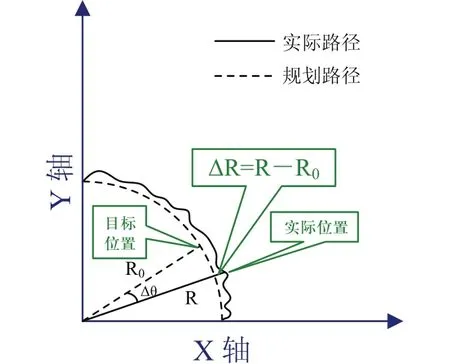
圖5 弧線跟蹤示意圖

e = D R + k × Dq ，ΔR為實時測得的半徑和規劃給出的半徑之差，Δθ為規劃的圓弧計算出的應轉的角度和由雙編碼器計算反饋回來的自身角度之差。如圖3所示，計算實時車體運動半徑公式如下：

其中：半徑R為OM的長度。

具體應用時，應根據事先給定的弧線路徑信息，先計算得出左右兩輪的初始基速度，兩者應該對應成比例，再此基礎上運用增量PID算法對跟蹤過程中產生的總誤差e進行調節。要實現快速轉弧，在高速且轉角較大度時，還應逐漸增大兩輪的差速，并在距目標角度還有一定的誤差時，逐漸減小兩輪差速以實現行走過程的流線銜接和平穩過渡[4]。

4 終點準確定位

通過直線和弧線的組合就可以控制機器人走復雜的路徑。最后停車時由于場地摩擦系數的不確定性，即使在到達終點附近就開始減速，由于慣性機器人可能往往會超過設定的終點才停下來，所以終點準確定位不像行走過程中的那樣只把左右輪差速作為被控對象，而機器人的左右輪差速和左右輪基速度都成了被控量。機器人的初始基速度是根據實際情況事先設定的。在終點準確定位控制中，都采用閉環PID控制。控制框圖如圖6所示。

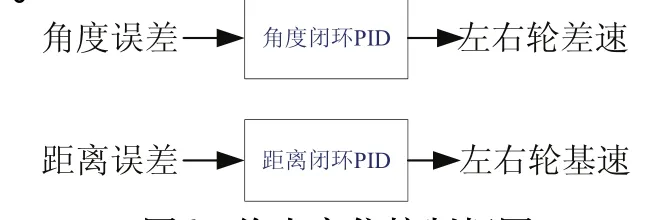
圖6 終點定位控制框圖

5 實驗結果和分析

表2 機器人跟蹤軌跡誤差比較（10次測試的實驗結果）

由測試結果可以看出，基于雙編碼器計算角度和距離控制機器人跟蹤事先設定好的路徑的方法可行，平均誤差都在100mm以內，基本可以滿足競賽機器人要求。在測試過程中，由于左右輪電機控制盒發送速度需要時間，所以控制程序的控制周期設定較大，在20ms左右，使控制效果得不到充分實現。另外左右兩個電機控制盒的速度不能被同時設定，所以在控制周期內輪流改變對兩個控制盒的發送順序，可以改善控制效果。

[1] 李世華,田玉平.移動小車的跟蹤控制[J].控制與決策,2000,15(5): 626-628.

[2] 鮮浩,任愛芝,盛仲飚.增量式編碼器數據采集[J].華北工學院學報,2003,24(2):142-143.

[3] 吳衛國,陳輝堂,王月娟.移動機器人的全局軌道跟蹤控制[J].自動化學報,2001,27(3):326-331.

[4] 龔建偉,陸際聯,黃文宇.輪式移動機器人航向跟蹤預估控制算法[J].機器人,2001,(3):193-196.