基于某民營商行數據的統計分析

湖北科技學院 張吉剛 梁娜

在當前的經濟生活和社會環境中，商行、商店這類經濟實體占據著舉足輕重的位置，它們是整個社會框架的基石，是最基層、數量最大的群體，研究它應有的發展規律，既能反映出以它為代表的中小企業經濟實體的發展趨勢，又幫助決策者進行分析、決策管理，從而促進商品的銷售，發現未知的商機，以獲取更多的利益。

針對某民營商行2012年的日銷售數據，先利用聚類分析對各類商品的月銷售量進行聚類，對每類提出相應的建議，再以各類商品的周銷售量為參考序列，建立時間序列模型，在此基礎上對2013年商品銷售量的趨勢進行預測。

1 月銷售額的聚類分析

為獲取完整的商品銷售數據信息，研究對象選擇使用條形碼、編碼系統、銷售管理系統、POS機的某個民營商行，選取該商行2012年6類商品，共計190836條銷售數據，以7天為一個銷售周期，即以636條周銷售數據為分析對象。6個品類分別為：香煙、酒、飲料、副食、農產品、生活用品(單位分別為包、瓶、袋、斤、件，為了統一計量單位，按單件記)。

各類商品年銷售額占總銷售額的比重：香煙占總銷售額的比重最大為35%，酒占總銷售額的28%，飲料占總銷售額的12%，副食、農產品和生活用品分別占總銷售額的8%、9%、8%。由此看出該民營商行最創收入的商品是煙酒。

采用系統聚類法中的類平均法。類平均法先從單個對象開始，開始時有多少個對象就有多少個類。將那些最相似(平均距離最短)的對象首先聚為類，然后根據類間的相似性把類進行合并，最后隨著相似性不斷下降，所有類漸漸融合為一個大類。本文把各月銷售額進行聚類，首先把業績最為接近的月份聚為類，聚類過程如表1所示。

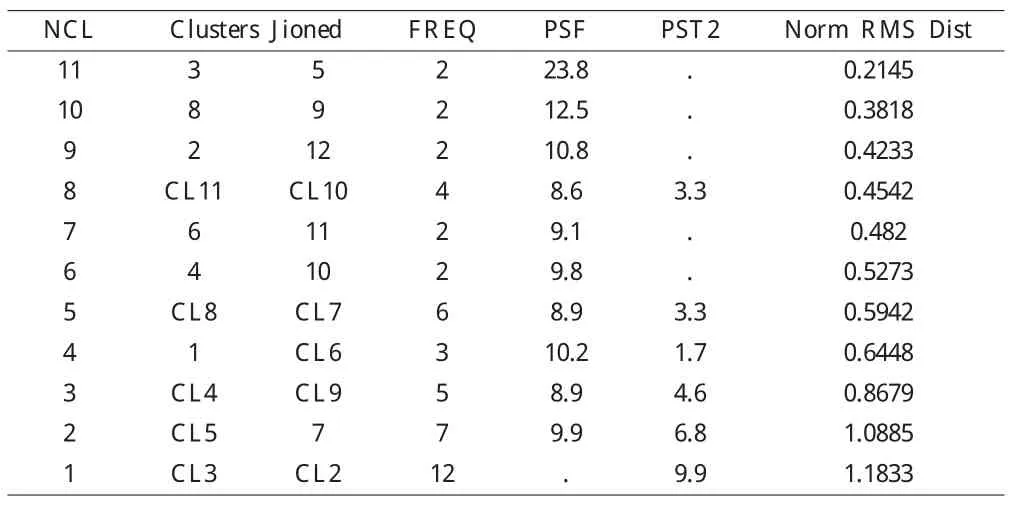
表1 聚類過程

由表1可知，偽F統計量在聚為4類時值最大為10.2；月銷售額從聚為3類到聚為4類時，偽統計量的值有很大的下降，且在4類時，該值最小為1.7統計量的值標準化均方根距離增加的幅度最大，由0.6448增加到0.8679，綜合判斷月銷售額最合適聚為4類。

第一類：1、10月，依托春節和國慶節的節日優勢帶動居民大量消費，是商行銷售業績最好的月份。2012年的大年三十在2月9號，年前1月人們都大量采購并儲備商品，六類商品的銷售額均非常可觀。10月有一個重要的節日——國慶節，7天假期，

第二類：7月，依靠季節優勢成為商行銷售大月。酒和飲料成了7月最受歡迎的商品，加上煙不離酒，煙的銷量也不低，僅憑這三類商品給商行帶來了較好的收益。

圖1 月銷售額的譜系圖

第三類：2、4、12月，伴隨著節日的末梢和年的終結，成為商行的銷售量下滑月。一般在節末和年尾，人們還有很多未消耗完的商品，暫時不需要再購買，商行的銷售額逐漸下降。另外，4月清明節祭祀，人們為了風俗必須購買一些必備品，同時準備少量酒食，商行的銷售額才得以保持。

第四類：3、5、6、8、9、11月，這段時間由于沒有什么大型節日帶動消費，季節的影響也不再明顯，于是，人們的消費需求進入一個低迷時期，商行的銷售額隨之達到低谷。

2 基于商行銷售額的ARMA建模及預測

2.1 商行銷售額時序平穩性檢驗

以商行2012年共53周的銷售額數據為原始的時間序列，并用時間序列分析軟件SAS作為工具，按照ARMA建模流程對其進行預測分析。

自相關圖(圖2)顯示該序列的自相關系數一直都比較小，始終控制在2倍的標準差范圍以內，可以認為該序列自始至終都在零軸附近波動，是隨機性較強的平穩時間序列。

2.2 模型定階與參數估計

對于ARMA(p,q)模型，可以利用其樣本的自相關函數和樣本的偏自相關函數的截尾性判定模型的階數。序列偏自相關圖如圖3所示。

圖2 銷售額序列自相關圖

圖3 銷售額序列偏自相關圖

圖2自相關圖顯示延遲2階之后，自相關系數全部衰減到2倍標準差范圍內波動，且由非零相關系數衰減為小值波動的過程非常突然，該自相關系數可視為2階截尾；圖3偏自相關圖顯示序列由顯著非零的相關系數衰減為小值波動的過程相當連續、相當緩慢，該偏自相關系數可視為不截尾。由此用MA(2)模型進行擬合。為了盡量避免個人經驗不足導致的模型識別問題，根據SAS系統提供的相對識別模型進一步識別，獲得一定范圍內的最優模型定階。根據ARMA模型的BIC信息量達到最小的模型選擇最合適的階數。

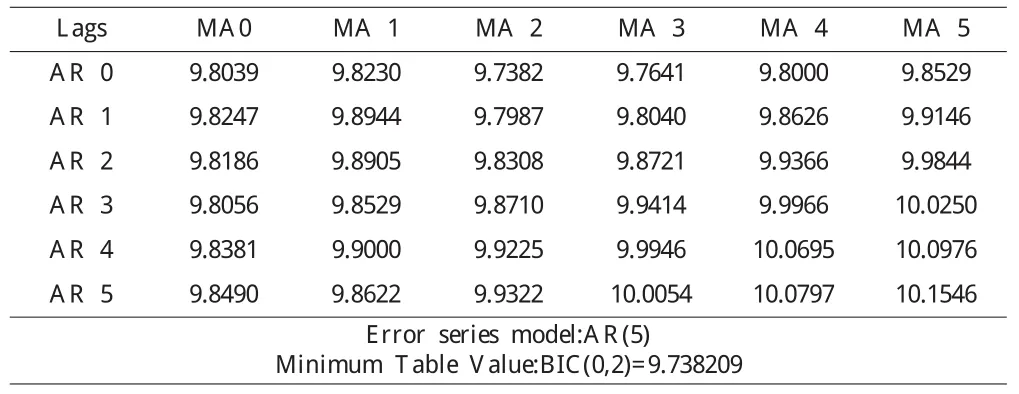
表2 ARMA模型的BIC信息量

在自相關延遲階數小于等于5，移動平均延遲階數也小于等于5的所有ARMA(p,q)模型中，BIC信息量相對最小的是ARMA(0,2)模型，即MA(2)模型。采用條件最小二乘估計，模型ARMA(0，2)中未知參數。

輸出的擬合模型形式：

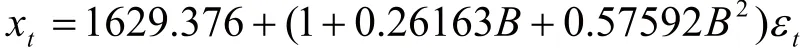
將當前序列值表示為隨機干擾項的函數表達式可記為：

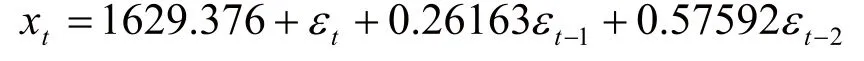
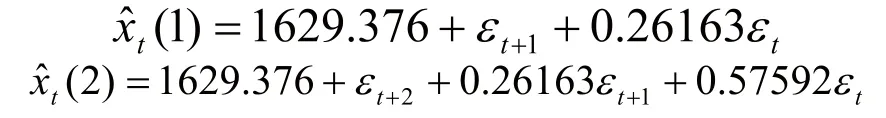
2.3 模型的有效性檢驗

模型的有效性檢驗即為殘差序列的白噪聲檢驗，殘差序列白噪聲檢驗結果如表3所示。殘差白噪聲檢驗顯示延遲6階、12階、18階、24階LB檢驗統計量的P值均顯著大于0.05，所以MA(2)模型顯著有效。

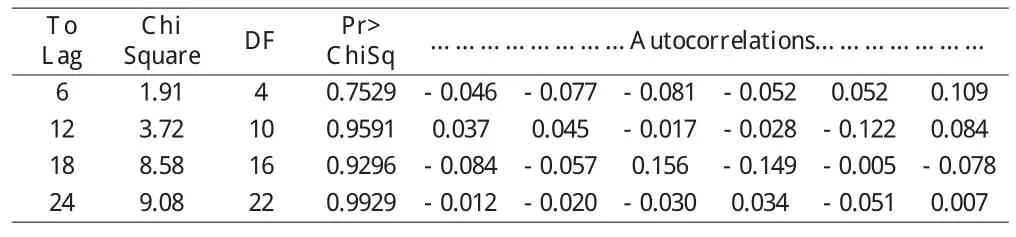
表3 殘差白噪聲檢驗結果

表4 參數顯著性檢驗結果

參數顯著性檢驗結果顯示三參數t統計量的P值均小于0.05，即三參數均顯著。因此MA(2)模型是該序列的有效擬合模型。

2.4 商行銷售量預測

利用ARMA(0，2)模型預測該商行2013年第1、2周的銷售額，與其真實值進行比較，結果如表5所示。

表5 ARMA(0，2)模型預測結果

由表5可知，2013年第1周、第2周的銷售額預測值與實際值的相對誤差均小于3.25%，ARMA模型預測精度較高；預測值與實際值趨勢一致，有略微遞減的趨勢；2013年2周的銷售額均高于2012年的平均水平1624元，說明該商行2013年銷售水平在提升。

3 結論

基于某民營商行2012年12個月的6類商品銷售數據，利用聚類分析法將月銷售額，分為4類：銷售額最高的1月和10月，銷售額較高的7月，銷售額持平平均值的2、4、12月，銷售額，銷售額處于淡季的3、5、6、8、9、11月。對于銷售額較好的1月、7月和10月，采取一定的促銷手段，清理積壓商品，增加商品銷售額。

本文利用ARMA模型在時間序列短期預測上的優勢，對該商行2012年53周6類商品銷售數據，建立了ARMA(0，2)模型，對ARMA 模型定階、參數估計、模型檢驗和模型預測進行了系統分析，預測了2013年第1、2周銷售額，并與實際值對比分析，最大誤差為3.25%，ARMA模型預測預測精度較高，對周銷售額作短期預測。

[1]高惠璇.應用多元統計分析[M].北京大學出版社,2005.

[2]黨姬男.ARMA時間序列模型在銷售預測中的應用[J].應用技術與研究,2009(8).

[3]王燕.應用時間序列分析[M].中國人民大學出版社,2009.

[4]張吉剛,梁娜.基于ARIMA-ANN的時間序列組合預測模型[J].三峽大學學報,2008(8).