線性回歸分析法在正交試驗中的應用

范步高

(上海長征富民金山制藥有限公司，上海201506)

正交試驗數據處理的常用方法一般有極差分析 (直觀分析)和方差分析。極差分析簡便、直觀，但不能區分指標的差異究竟是因子的水平變化所引起還是由試驗的誤差所引起，故極差分析的準確性較低，所以，為提高正交試驗結果分析的準確性應首選方差分析。但正交試驗的方差分析一般須預留空白列 (誤差列和交互作用列)，代價是試驗總數增加或減少獨立因子數，否則，正交試驗方差分析的準確性也將大大降低，此時較為理想的選擇則應是“線性回歸分析法”［1-4］。

1 實例分析

《中成藥》2011年 (第33卷)第7期第1206頁載文“正交設計法優選苦參炮制工藝的研究”［5］(以下簡稱原文)，原文目的是優選苦參的切制工藝，選用L9(34)正交表進行優選，現將原文的表2(因素和水平考察)、表3(苦參炮制工藝正交試驗結果)和表4(苦參炮制工藝方差分析)合并為本文的表1，原文直觀分析 (極差分析)與方差分析得出的最佳條件與直接觀察法相同，均為A1B3C3，即第3號試驗，Y3=Ymax=1.831，因素重要性排序為A＞C＞B。3批驗證結果:苦參堿和氧化苦參堿指標分別為 1.83%、1.80%、1.82%，均值為 1.82%，RSD為0.64%。

1.1 方差分析的正確計算 原文為3因子3水平，選擇L9(34)正交表，前提條件應是因子間無兩兩交互作用或兩兩交互作用可以忽略不計，另外3因子排畢還應剩余“空列”1列，可以作為誤差項進行方差分析 (原文將“空列”遺漏，故計算有誤)，因B和C因子的均方差均小于“空列”，為防止誤判因子的顯著性，提高方差分析的準確性，故合并三列為誤差項 (SS空+SSB+SSC=SSe)。結果見表2。

表1 原文苦參炮制工藝正交試驗結果分析

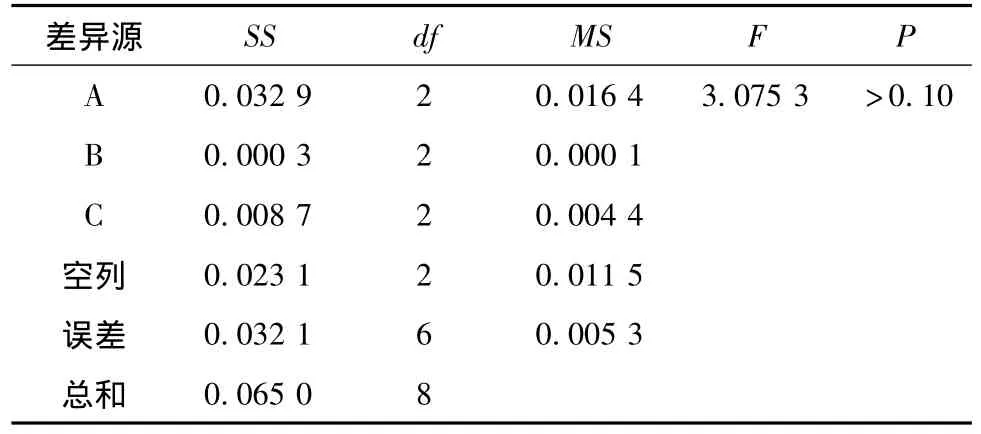
表2 苦參炮制工藝正交試驗方差分析

由表2可知，因素A、B、C水平的變化對指標的影響均不顯著 (與原文結論差異較大)，即差異較多是由試驗誤差過大所引起。所以，對不顯著因子的水平優選一般不是選擇相對較高指標值所對應的水平，而是綜合考慮該水平在實際生產中的生產周期、能耗、質量可控性等情況而選定。所以，若綜合考慮苦參炮制工藝的最佳條件應首選A1B1C1(浸泡20 min，軟潤16 h，60℃干燥)，即該輪L9(34)正交試驗中第1號試驗，Y1=1.732，低于第3號試驗指標值Y3=1.831，但此結果僅僅是在因子間無兩兩交互作用或兩兩交互作用可以忽略的前提下。根據L9(34)正交表任意兩列間的交互作用列為另外兩列，現存在MS空＞MSC＞MSB，故原文前提條件不成立，即 A、B、C因子的兩兩交互作用不可忽略。

表2結果可由表1原始數據用Excel統計函數計算得到［6］，也可仿照原文由簡單公式計算:T=ΣYi=26.512，CT=T2/n=26.447;總平方和SST=T2－CT;A、B、C及空列(第4列)平方和SSjCT。對規格化正交表存在等式:SST=Σ SSj，可以用于檢驗計算的正確與否。

1.2 線性回歸分析及預測 對三水平的A、B、C因子間的交互作用，解決的辦法可以重新選擇較大的L18(37)或L27(313)正交表再進行一次有交互作用的正交試驗進行優選，也可以在原L9(34)正交試驗的基礎上，利用多元線性回歸分析法進行工藝優選和結果預測。

1.2.1 多元線性回歸分析模型構建 根據正交試驗的方差分析結果，假設A、B、C存在較強的兩兩交互作用AB、AC和 BC，回歸子集大小為六元 (A、B、C、AB、AC、BC)，線性回歸模型為Y*=b0+b1A+b2B+b3C+b4AB+b5AC+b6BC，經用矩陣法求得各因子的偏決定系數 (偏相關系數的平方)進行顯著性檢驗和篩選，“最優”子集為五元 (A、B、C、AB、AC)、“次優”子集為四元 (B、C、AB、AC)(表3，表4)。

表3 線性回歸“最優”子集Excel篩選模型

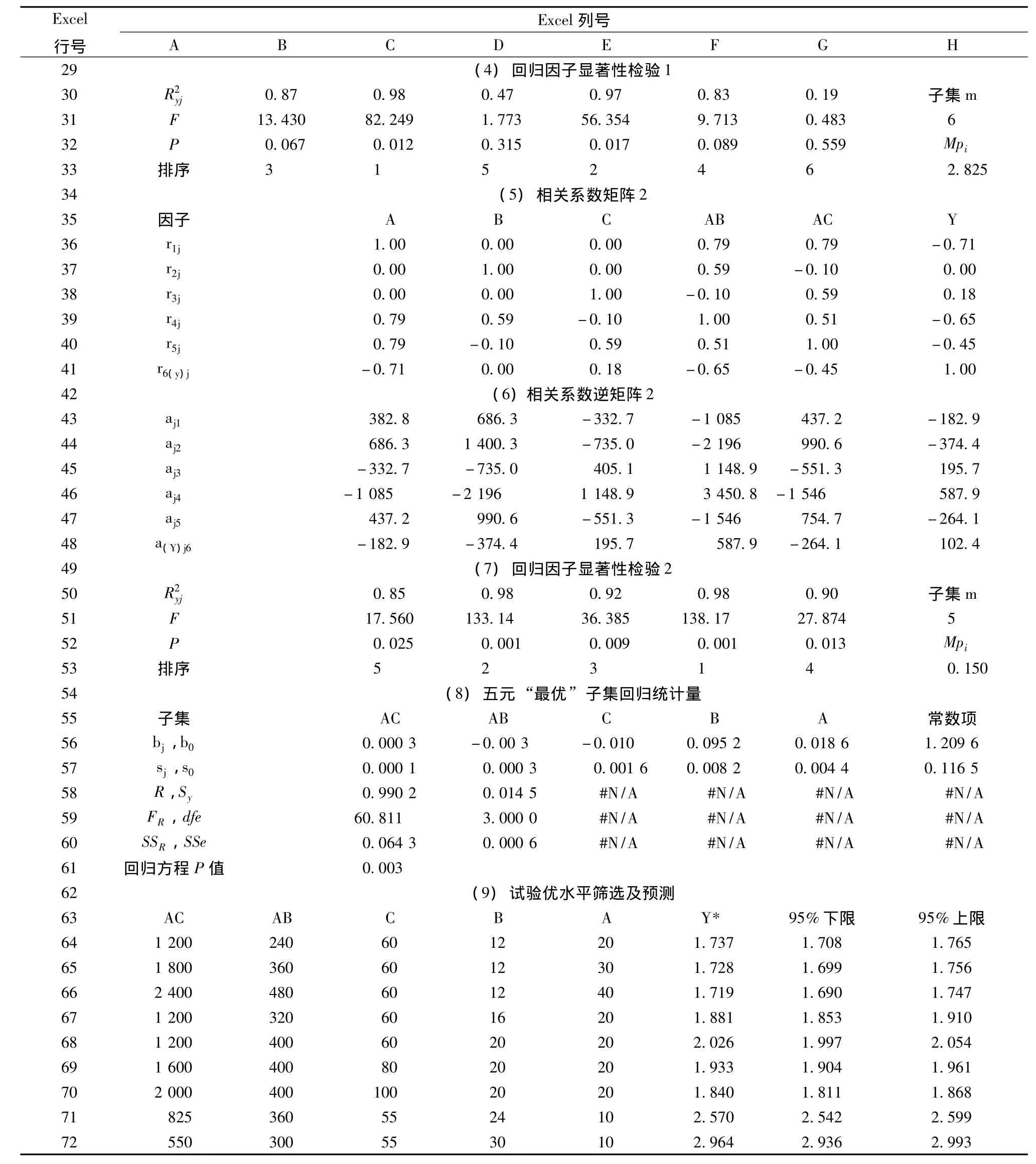
(續表3)

表4 線性回歸“最優”子集篩選結果

1.2.2 線性回歸分析結果及置信區間 由表3可得五元“最優”線性回歸方程為 Y*=1.209 6+0.018 6A+0.095 2B－0.010 0C－0.003 0AB+0.000 3AC，回歸標準誤差Sy=0.014 5，回歸方程顯著性P值＜0.01，各回歸因子顯著性Pj值＜0.05，因子重要性排序AB＞B＞C＞AC＞A。對原文優選水平A1B3C3進行預測，均值落在其預測區間內(表3)，證明回歸方程的預報可信。參考方差分析結果，經多次單因素試驗回歸得優選水平為A1B3C1(浸泡20 min，軟潤20 h，60℃干燥)，此水平組合未包含在L9(34)正交試驗中，故需進行至少3批的驗證試驗加以確定，其驗證試驗結果預測值約為2.026%，95%置信區間在1.997%～2.054%，高于第3號正交試驗 (A1B3C3)最高值Y3=1.831%(見表3)。

1.2.3 表3中Excel函數或公式設置

(1)試驗因子及交互項水平數據與指標結果:A、B、C及Y數據可直接輸入，交互作用的因子數據利用乘法公式輸入，E3=B3×C3(意即E3單元格輸入“=B3×C3”，下同)，F3=B3×D3，G3=C3×D3，分別確認后選中E3∶G3，向↓拖曳復制至G11。

(2)相關系數矩陣1:B14=CORREL(S|BS|3∶S|BS|11，BS|3∶BS|11)，確認后選中并向↓拖曳復制至B20，并從B15起依次將S|BS|3∶S|BS|11中的列號B分別修改為C、D、E、F、G、H，分別確認后選中B14∶B20，向→拖曳復制至H列。

(3)相關系數逆矩陣1:選中B22∶H28(區域大小須與B14∶H20矩陣相同)，輸入:=MINVERSE(B14:H20)，三鍵確認 (一般特定公式或數組公式輸入均需shift+ctrl+enter三鍵確認，當判別有疑時也可用三鍵確認解決，下同)。

(4)回歸因子顯著性檢驗1:偏決定系數B30=B28^2/B22/S|H28(若求偏相關系數，B30=－B28/SQRT(B22/S|H28))，偏回歸因子F值B31=B30/(1－B30) × (9－S|H31－1)，偏回歸因子 P值 B32=FDIST(B31，1，9－S|H31－1)，偏回歸因子重要性排序 B33=RANK(B30，S|B30:S|G30)，分別確認后選中B30∶B33，向→拖曳復制至G列。Mpi統計量 H33=SUM(B32:G32)/H31× (9+H31+1)。

(5)相關系數矩陣2:根據回歸因子顯著性檢驗1的結果，去掉相關系數矩陣1中最不顯著因子BC(第六行及第六列數據)，利用等號將剩余標志和數據“移植”，如C35=B13，C41=B20。為方便回歸因子顯著性檢驗公式無需修改地重復使用，需將原相關系數矩陣1中第七行數據上移至第六行、原第1～5列數據整體右移。

(6)相關系數逆矩陣2:選中C43∶H48，輸入=MINVERSE(C36:H41)，三鍵確認。

(7)回歸因子顯著性檢驗2:復制表3(4)，清除B50∶B53，修改子集m大小，H53復制H33后粘貼。

(8)五元“最優”子集回歸統計量:選中5行 (m+1)列即 C56∶H60，輸入:=LINEST(S|HS|3∶S|HS|11，S|BS|3∶S|FS|11，TRUE，TRUE)，三鍵確認。回歸方程P值:C61=FDIST(C59，9-1-D59，D59)

(9)試驗優水平篩選及預測:利用多次單因素試驗進行優水平篩選，并假設殘差服從正態分布，U0.05=1.96，則95%置信度預測值誤差=1.96×Sy，所以，預測值F64=SUM(S|CS|56∶S|GS|56×A64∶E64)+S|HS|56，三鍵確認;95%下限值G64=S|F64－1.96×S|DS|58，95%上限值H64=S|F64+1.96×S|DS|58，分別確認后選中F64∶H64，并向↓拖曳復制至行72。

對于確定的“最優”子集，偏回歸系數等回歸統計值也可以直接利用Excel回歸分析工具自動求出，可以作為對以上顯著性檢驗計算正確與否的檢驗 (自動給出的偏回歸系數t檢驗與回歸因子的偏決定系數的F檢驗等值)，方法是:分別點擊Excel工具→數據分析→回歸分析→確定，填寫回歸對話框，Y值區域輸入S|BS|1∶S|BS|10，X值區域輸入S|CS|1∶S|GS|10，勾選“標志”，點選“輸出區域”，點擊B73，點擊確定，即可得到更為詳細的回歸分析結果 (略)。

2 討論

2.1 工藝優化水平的確定 對q個水平m*個獨立回歸因子的線性回歸方程進行優化工藝水平的確定，既可采用qm*次單因素試驗法，也可采用更為準確的qm*次全面試驗法或“規劃求解法”［3］，也可以采用“極值法”{4}或根據方程的復雜程度靈活組合應用，如五元“最優”線性回歸方程Y*=1.209 6+0.018 6A+0.095 2B－0.010 0C－0.003 0 AB+0.000 3AC，若求其極值較為不易，但在試驗水平考察范圍內有A↘Y*↗ (Y*對A的一階偏導小于零)、C↘Y*↗ (Y*對C的一階偏導小于零)和B↗Y*↗ (Y*對B的一階偏導大于零)的單調性趨勢［9］，所以，Y*最大值所對應的優化水平可選定為A1B3C1，這也與一般中藥的穩定性規律 (低溫干燥有利于減少氧化、分解等反應對中藥有效成分群所造成的損失)和苦參堿及氧化苦參堿的理化性質 (極性大，易水溶，易水解)相吻合。

多次單因素試驗法是先固定 (m*－1)個獨立因子的水平并與另一因子的各個水平進行q次全搭配預測，根據預測結果得出該因子的較優水平并固定，然后更換下一個獨立因子重復上述全搭配預測，直至進行qm*次 (包括m*－1次重復)得出所有m*獨立因子的較優水平搭配即為回歸分析法的優選水平組合，但當回歸方程在水平考察范圍內存在拐點［9］時，不同水平的固定將會影響優選水平的準確性。

2.2 “最優”線性回歸方程的篩選準則 “最優”線性回歸方程的篩選準則通常有復決定系數R2、復相關系數R、回歸F值等愈大愈好，子集m、殘差平方和SSe、平均殘差平方和 MESS(均方 MSe)、平均預測均分誤差 MPESS、AIC準則、BIC準則等愈小愈好［7-8］。本文的篩選方法或步驟:①選擇“最優”子集m，使m子集內的各個因子的顯著性Pj值均小于0.05或0.10，②根據m“少而精”之原則，設定統計量Mpi=(n+m+1)×ΣPj/m，選擇Mpi最小子集;③選擇線性回歸方程的顯著性P值小于0.05的“最優”子集 (各因子顯著性Pj值均小于0.05的“最優”子集，其對應的線性回歸方程的顯著性P值一般也小于0.05，反之，則可能性降低，需要進一步對各因子進行顯著性檢驗加以確定)。

對于三獨立因子 (m*=3)試驗，其二次多項式回歸因子 (一次項、二次項、交互項)共有 9項，若一次項A、B、C和交互項AB、AC、BC子集中未能在表3模型中篩選出“最優”子集，可以將二次項A2、B2、C2回歸因子替換表3相關系數矩陣1中最小偏決定系數對應的回歸因子或其他因子 (可以重復使用復制、粘貼、撤銷鍵，表中公式無需修改)進行篩選。

回歸因子m要求“少而精”，實則是要求“最優”線性回歸方程內的自變量因子均為顯著因子，而方程外的所有因子均為不顯著因子，同時也可以認為是要求線性回歸方程的殘差自由度 (離回歸自由度)盡可能的大 (dfe=n－m－1)，目的是避免擬合的方程回歸不錯 (殘差較小)，預報不好 (驗證試驗結果誤差較大)，其解決的辦法是增加觀察值 (試驗次數)以達到n≥2m或至少保證殘差自由度(n－m－1)≥2。

2.3 正交試驗數據處理方法的選擇

正交試驗的目的，①是考察各因子的水平差異對指標值影響的相對大小，②是篩選最優化試驗條件。

極差分析計算最為簡單，可達①之目的，但極差分析未及消除試驗誤差對指標值的影響，故其極差較大的主要因子未必是顯著因子［10］。所以，欲達②和①之目的，經典的方差分析則較為準確，應為首選。

在進行正交試驗的Ln(qm)正交表中，獨立因子各占1列，交互因子各占 (q－1)d列 (一般僅考慮兩兩交互作用，其交互作用級數d=2－1)，誤差項也至少須占1列(空列)，根據n(試驗總次數或正交表行數)、q(因子水平數)和m(因子列數或正交表列數)三者存在n=qk或n=sq2(k=2，3，4，…，s=1，2，3，…)或n=m(q－1)+1的關系式［11］可知，m和q增加，n將呈番數或指數增長，結果是造成試驗成本大大增加。所以，正交試驗的方差分析也僅在因子間沒有交互作用或交互作用可以忽略，或者獨立因子數和水平數均較少時較為實用。

線性回歸分析與方差分析都是研究數據的統計方法，線性回歸法常用于均勻設計，方差分析法則常用于正交設計，但當正交設計的獨立因子 (自變量，非隨機變量)為連續性變量且與指標變量 (因變量，隨機變量)存在顯著線性關系時也可以采用線性回歸分析法［12］，其優點之一是正交表的m列可以排滿獨立因子而達包括交互因子優選水平在內的②和①之目的，二是根據正交試驗信息量可以較為方便的構建線性回歸模型，用于工藝過程預測和控制，并能指導超越正交試驗原有水平的考察范圍捕捉到更優化的工藝條件，如上述優選水平A1B3C1，均為“邊界”水平組合，在進行驗證試驗時，可以根據實踐經驗同時考慮選擇小于A1(如A0:浸泡10min)或C1(如C0:55℃真空干燥)或大于B3(如B4:軟潤24 h)的水平組合進行對照。經預測，A0B4C0苦參炮制工藝更優，回歸預測值為2.570%，95%置信區間在2.542% ～2.599%，高于原優選水平A1B3C1的預測值2.026%(表3)，這也是線性回歸分析優于正交試驗方差分析的一個結果體現。

［1］李云雁，胡傳榮．試驗設計與數據處理［M］．北京:化學工業出版社，2005．

［2］胡譽滿，謝曉鳴．利用回歸分析對正交試驗試驗結果進行修正［J］．工科數學，2000，16(4):32-34．

［3］俞鐘行．質量工程師教材例2.3-1新解［J］．質量春秋，2011(11):48-351．

［4］郭俊旺，劉曉峰，魏彩云．正交設計L9(34)的漸進優化線性回歸方法［J］．計算機與應用化學，2010，27(11):1503-1508．

［5］鄧捷圓，胡 馨，張英華，等．正交設計法優選苦參炮制工藝的研究［J］．中成藥，2011，33(7):1206-1208．

［6］范步高．正交試驗方差分析的Excel通用計算與應用［J］．中國醫藥工業雜志，2011，42(10):793-795．

［7］李東風，鄭忠國．最優線性回歸的計算方法［J］．數理統計與管理，2008，27(1):87-95．

［8］丘冠英．“最優”回歸方程的選擇準則和具體方法［J］．宜春學院學報:自然科學，2003，25(6):26-27．

［9］王順鳳，夏大峰，朱鳳琴，等．高等數學(上)［M］．北京:清華大學出版社，2009．

［10］郝拉娣，張 嫻，劉 琳．科技論文中正交試驗結果分析方法的使用［J］．編輯學報，2007，19(5):340-341．

［11］全國質量專業技術人員職業資格考試辦公室．質量專業理論與實務(中級)［M］．北京:中國人事出版社，2006．

［12］喬克林，呂 佳．方差分析與回歸分析之比較［J］．延安大學學報:自然科學版，2009，28(2):34-36．