非線性彈性地基上懸臂輸流管的受迫振動(dòng)

張紫龍，唐 敏，倪 樵

(華中科技大學(xué) 力學(xué)系，武漢 430074;工程結(jié)構(gòu)與安全湖北省重點(diǎn)實(shí)驗(yàn)室，武漢 430074)

輸流管是一種廣泛應(yīng)用于油氣運(yùn)輸、采礦工程、熱交換器等工程領(lǐng)域中的重要工程結(jié)構(gòu)。眾所周知，當(dāng)管內(nèi)流速大于某一臨界值時(shí)，輸流管將會(huì)發(fā)生失穩(wěn)，失穩(wěn)形式與端部支承方式有關(guān)(對(duì)于兩端支承輸流管，將發(fā)生屈曲失穩(wěn);而對(duì)于懸臂輸流管，將發(fā)生顫振失穩(wěn))。一旦輸流管道發(fā)生失穩(wěn)，可能會(huì)對(duì)整個(gè)結(jié)構(gòu)造成破壞。因此，近幾十年來輸流管的動(dòng)力學(xué)行為已經(jīng)成為結(jié)構(gòu)動(dòng)力學(xué)研究的重要內(nèi)容之一，許多研究者［1-11］對(duì)這一問題進(jìn)行了研究。已有研究表明［12-14］，地基的力學(xué)特性對(duì)輸流管系統(tǒng)的動(dòng)力學(xué)行為有很大的影響。常用的彈性地基近似模型主要有兩種［15］:① Winkler模型，該模型不考慮土體的連續(xù)性，將地基等效為一系列相互獨(dú)立的線性彈簧系統(tǒng)，地基上任一點(diǎn)受力只有該點(diǎn)處的彈簧產(chǎn)生形變，其他彈簧不受影響;② Pasternak雙參數(shù)模型，該模型在Winkler模型基礎(chǔ)上考慮了土體的剪切效應(yīng)和連續(xù)性，相對(duì)于Winkler模型，該模型更接近實(shí)際情況。基于以上兩種地基模型，許多研究者對(duì)彈性地基上輸流管道的動(dòng)力學(xué)行為進(jìn)行了研究。王忠民等［16］研究了以上兩種地基模型上的輸流管道的振動(dòng)穩(wěn)定性，并分別討論了兩種地基模型中各參數(shù)對(duì)系統(tǒng)穩(wěn)定性的影響。Doared等［17］基于Winkler地基模型研究了彈性地基上懸臂、兩端簡(jiǎn)支等支承作用下輸流管道的局部和全局穩(wěn)定性。Qian等［18］基于Winkler模型，使用三次非線性彈簧來描述地基的非線性特性，建立了非線性雙參數(shù)Winkler模型，在此基礎(chǔ)上研究了非線性彈性地基上懸臂輸流管的非線性動(dòng)力學(xué)行為，并討論了各參數(shù)對(duì)系統(tǒng)Hopf分岔點(diǎn)流速的影響，結(jié)果顯示地基的非線性剛度對(duì)于系統(tǒng)的非線性動(dòng)力學(xué)行為有重要的影響，在研究輸流管-地基系統(tǒng)的非線性動(dòng)力學(xué)行為時(shí)不應(yīng)忽略。梁峰等［19］研究了Pasternak雙參數(shù)彈性地基上兩端固支輸流管道的靜態(tài)和動(dòng)態(tài)穩(wěn)定性問題，并應(yīng)用平均法考察了脈動(dòng)內(nèi)流作用時(shí)管道的前兩階主參數(shù)共振和組合共振，結(jié)果表明，地基的剪切剛度對(duì)輸流管-地基系統(tǒng)的靜態(tài)和動(dòng)態(tài)穩(wěn)定性均有顯著影響。

為了更真實(shí)地反映彈性地基上輸流管的動(dòng)力學(xué)特性，本文基于Pasternak雙參數(shù)地基模型，綜合考慮地基的剪切效應(yīng)、非線性特性和粘滯阻尼的影響，建立了基礎(chǔ)激勵(lì)作用下非線性彈性地基上輸流管的運(yùn)動(dòng)方程。使用Galerkin法，研究了基礎(chǔ)激勵(lì)作用下非線性地基上懸臂輸流管的非線性動(dòng)力學(xué)行為，著重討論地基剪切剛度和基礎(chǔ)激勵(lì)頻率對(duì)系統(tǒng)動(dòng)力學(xué)特性的影響。

1 運(yùn)動(dòng)方程

考慮圖1所示非線性彈性地基上的懸臂輸流管道，U為管內(nèi)流體流速，w(x，t)是管道中心線的橫向位移，x為沿管道長(zhǎng)度方向的位置坐標(biāo);kG，C，k1，k2分別表示地基的剪切剛度，粘滯阻尼，等效線性剛度，等效非線性剛度;Y0sin(Ωt)是基礎(chǔ)位移激勵(lì)。

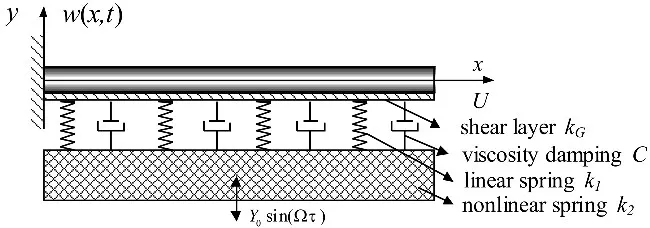
圖1 非線性彈性地基上懸臂輸流管道示意圖Fig.1 Schematic of a cantilevered fluid-conveying pipe rested on nonlinear Pasternak foundation

基礎(chǔ)激勵(lì)作用下非線性彈性地基上的懸臂輸流管道運(yùn)動(dòng)方程可寫作［18-19］:

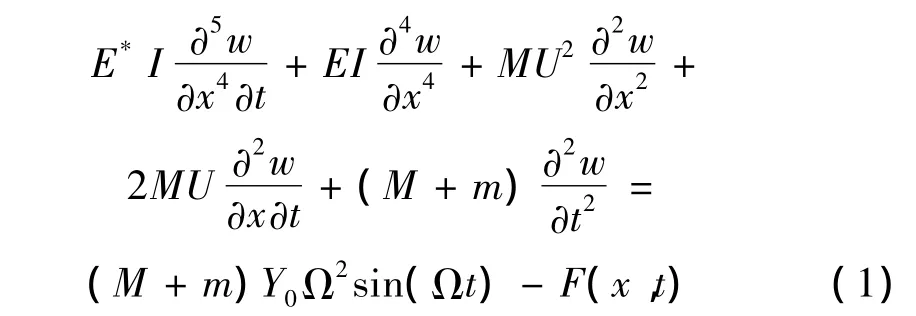
其中:EI為管道的彎曲剛度，E*為粘彈性系數(shù)，M和m分別表示單位長(zhǎng)度流體和管道的質(zhì)量，F(xiàn)表示單位長(zhǎng)度地基對(duì)管道的支承力。

對(duì)于圖1所示非線性彈性地基，其對(duì)管道的單位長(zhǎng)度支承力可表示為:

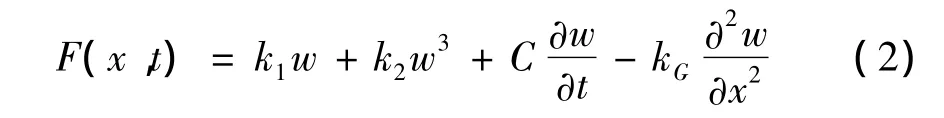
引入如下無量綱參數(shù)，l為管道的長(zhǎng)度，

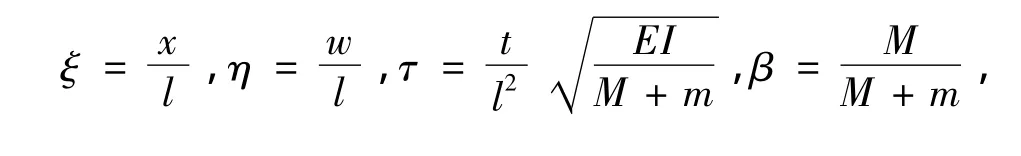
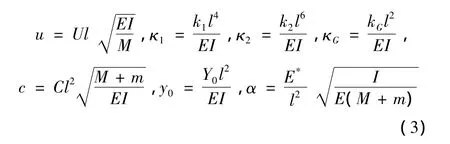
可以將式(1)寫成如下的無量綱形式:

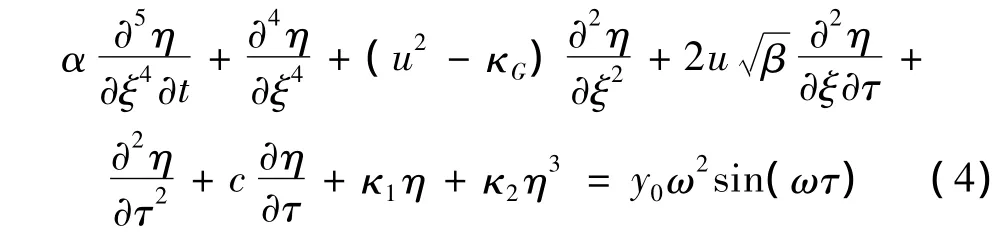
方程(4)可利用Galerkin法進(jìn)行離散。方程(4)中管道的位移函數(shù)可表示為:

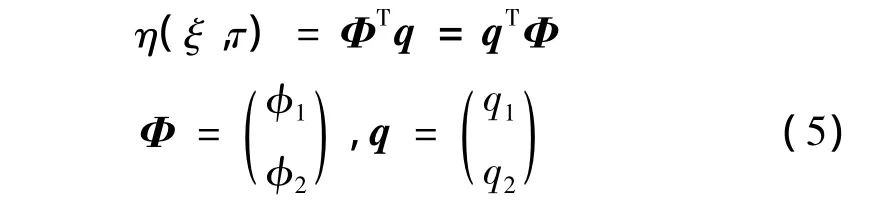
其中:φr，r=1，2是懸臂梁的模態(tài)函數(shù)，qr為廣義坐標(biāo)。將上式代入方程(4)，并在方程兩邊同時(shí)左乘Φ，然后對(duì)ξ從0～1積分，利用模態(tài)函數(shù)的正交性，可得:

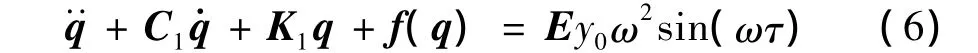
其中，I為單位矩陣。

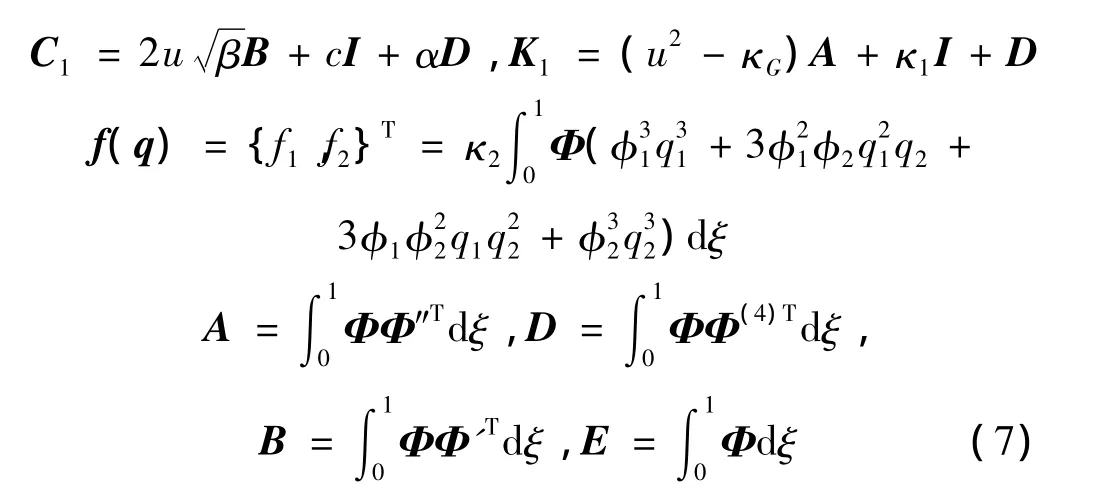
為了方便后續(xù)的數(shù)值計(jì)算，引入狀態(tài)向量z={q1，q2，1，2}，將式(6)寫成如下形式的一階狀態(tài)方程:

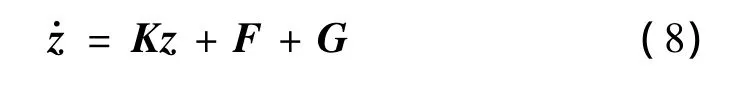
其中:

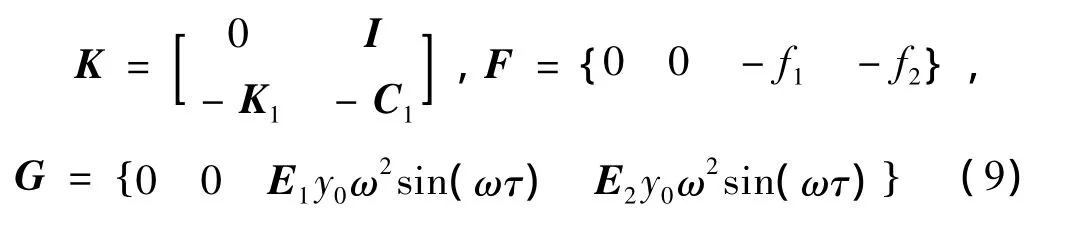
式(8)構(gòu)成了輸流管系統(tǒng)的非線性響應(yīng)控制方程，求解此方程可得到輸流管在取定參數(shù)下的動(dòng)力響應(yīng)。

2 數(shù)值仿真

為了分析輸流管系統(tǒng)的動(dòng)力響應(yīng)，重點(diǎn)考察管道自由端的響應(yīng)。采用四階Runge-Kutta法對(duì)方程(8)進(jìn)行求解，時(shí)間步長(zhǎng)取0.001，初始條件為 qi=0.001，i=0，i=1，2。在以下分析中，選取較高內(nèi)流速度，u=11。由文獻(xiàn)［18］可知，在不考慮外部激勵(lì)作用時(shí)，該流速下輸流管系統(tǒng)處于偏離零平衡位置的一個(gè)穩(wěn)定焦點(diǎn)。其余系統(tǒng)參數(shù)選取如下［18］:

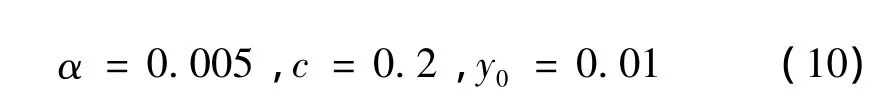
首先，考察地基剪切剛度κG=0時(shí)，系統(tǒng)在基礎(chǔ)激勵(lì)作用下的動(dòng)力響應(yīng)。圖2給出了以基礎(chǔ)激勵(lì)頻率ω為控制參數(shù)時(shí)的分岔圖，圖中縱坐標(biāo)是輸流管自由端(ξ=1)處的位移。當(dāng)管道端部位置的振動(dòng)速度為零時(shí)(η(1，τ)=0)，記錄此時(shí)管道端部位置的瞬時(shí)位移(η(1，τ)=φ1(1)q1(τ)+ φ2(1)q2(τ))，并將其以點(diǎn)的形式繪制到分岔圖中。在分岔圖的繪制中，并未考慮初始時(shí)刻的振動(dòng)過程，僅考慮振動(dòng)相對(duì)穩(wěn)定時(shí)的響應(yīng)。從該圖可以看出，隨著基礎(chǔ)激勵(lì)頻率的變化，地基-輸流管系統(tǒng)呈現(xiàn)出非常豐富的動(dòng)力學(xué)行為，包括周期、概周期和混沌運(yùn)動(dòng)。當(dāng)激勵(lì)頻率較小時(shí)，管道發(fā)生周期-1運(yùn)動(dòng)。當(dāng)37.5＜ω＜39.5時(shí)，系統(tǒng)處于混沌運(yùn)態(tài)。而當(dāng)39.5＜ω＜50.65時(shí)，系統(tǒng)發(fā)生周期-3振動(dòng)。隨著激勵(lì)頻率的增大，系統(tǒng)將在50.65＜ω＜51.5發(fā)生倍周期分岔并通向混沌，進(jìn)一步研究表明，此區(qū)域內(nèi)系統(tǒng)的振動(dòng)形態(tài)依次為:周期 -3，周期 -6，周期 -12，……，周期-3·2n-1，混沌。從圖中還可以看到，隨著激勵(lì)頻率的變化系統(tǒng)在某些頻率范圍內(nèi)會(huì)發(fā)生多次振動(dòng)形態(tài)的跳躍并最終過渡到混沌運(yùn)動(dòng)，比如在76.9＜ω＜78，系統(tǒng)的運(yùn)動(dòng)形態(tài)從周期-4跳躍到周期-13，然后跳躍到周期-4，又從周期-4跳躍到周期-11，…，并由此過渡到下一個(gè)混沌運(yùn)動(dòng)窗口。繼續(xù)增大激勵(lì)頻率，系統(tǒng)將會(huì)從混沌運(yùn)動(dòng)經(jīng)由概周期運(yùn)動(dòng)過渡到下一個(gè)周期運(yùn)動(dòng)窗口。值得注意的是，上述混沌運(yùn)動(dòng)窗口中均包含了多個(gè)周期和概周期窗口。圖3給出了典型運(yùn)動(dòng)形態(tài)的相軌跡圖，從中可以清楚地看到系統(tǒng)運(yùn)動(dòng)形態(tài)的變化情況，如圖3(d)～(f)是系統(tǒng)發(fā)生倍周期分岔的過程。

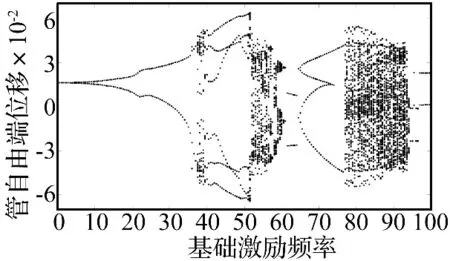
圖2 以基礎(chǔ)激勵(lì)頻率ω為控制參數(shù)的分岔圖，κG=0Fig.2 Bifurcation diagram for the tip point displacement，as a function of forcing frequency ω，for κG=0

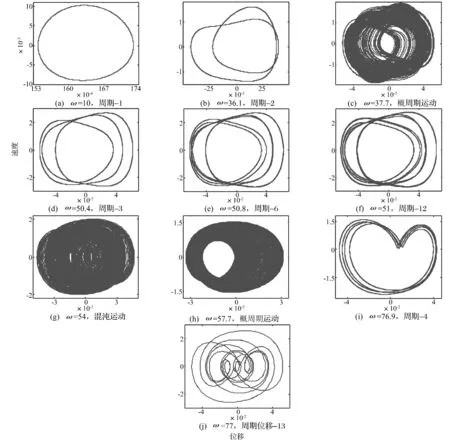
圖3 不同基礎(chǔ)激勵(lì)頻率下輸流管自由端運(yùn)動(dòng)形態(tài)的相軌跡圖Fig.3 Phase portraits of the motions of the tip point，for the system defined in Fig.2

接下來將研究地基剪切剛度對(duì)系統(tǒng)動(dòng)力學(xué)行為的影響，即κG≠0時(shí)。圖4～5給出了不同地基剪切剛度下系統(tǒng)的分岔圖。由圖2、圖4和圖5可以看出，地基剪切剛度對(duì)系統(tǒng)的動(dòng)力學(xué)行為有很明顯的影響，隨著地基剪切剛度的增大，系統(tǒng)的混沌運(yùn)動(dòng)和概周期運(yùn)動(dòng)窗口逐漸減小并消失。值得注意的是，當(dāng)?shù)鼗羟袆偠茸銐虼髸r(shí)(對(duì)于本文所取參數(shù)，κG=40)，系統(tǒng)在所取激勵(lì)頻率范圍內(nèi)將始終處于周期運(yùn)動(dòng)狀態(tài)。由此可見，地基剪切剛度對(duì)于基礎(chǔ)激勵(lì)作用下輸流管-地基系統(tǒng)的混沌運(yùn)動(dòng)和概周期運(yùn)動(dòng)有很好的抑制作用。這對(duì)于輸流管的振動(dòng)控制設(shè)計(jì)與實(shí)際應(yīng)用具有重要意義。因?yàn)閷?duì)于實(shí)際系統(tǒng)而言，混沌運(yùn)動(dòng)通常是有害的，在進(jìn)行輸流管設(shè)計(jì)和鋪設(shè)的時(shí)候，可以通過增加地基的剪切剛度來避免管道發(fā)生混沌運(yùn)動(dòng)，從而提高輸流管系統(tǒng)的安全性。

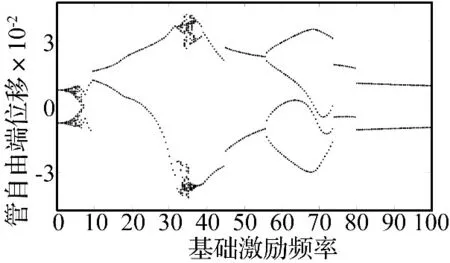
圖4 考慮地基剪切剛度時(shí)系統(tǒng)的分岔圖，κG=20Fig.4 Bifurcation diagram for the tip point displacement，as a function of forcing frequency ω，κG=20

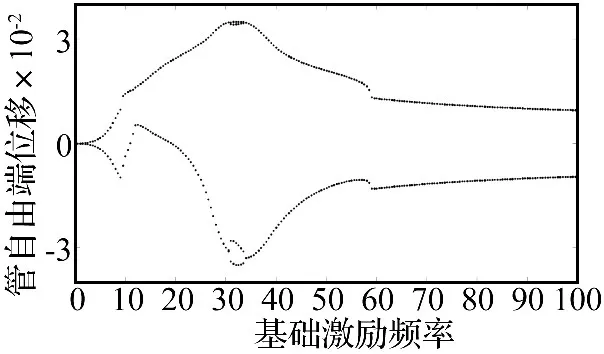
圖5 考慮地基剪切剛度時(shí)系統(tǒng)的分岔圖，κG=40Fig.5 Bifurcation diagram for the tip point displacement，as a function of forcing frequency ω，κG=40

3 結(jié)論

本文基于Pasternak地基模型，綜合考慮地基的剪切效應(yīng)、非線性特性和粘滯阻尼的影響，研究了基礎(chǔ)激勵(lì)作用下非線性彈性地基上輸流管的非線性動(dòng)力響應(yīng)，著重討論了基礎(chǔ)激勵(lì)和地基剪切剛度對(duì)系統(tǒng)動(dòng)力學(xué)特性的影響。數(shù)值計(jì)算表明，系統(tǒng)在基礎(chǔ)激勵(lì)作用下具有非常復(fù)雜的動(dòng)態(tài)響應(yīng)，包括多種形式的周期、概周期和混沌運(yùn)動(dòng)。當(dāng)基礎(chǔ)激勵(lì)頻率連續(xù)變化時(shí)，系統(tǒng)的運(yùn)動(dòng)形態(tài)還會(huì)發(fā)生跳躍。系統(tǒng)主要經(jīng)由以下兩種路徑通向混沌:倍周期分岔;運(yùn)動(dòng)形態(tài)的跳躍。其中后一種路徑與倍周期分岔類似，但其運(yùn)動(dòng)形態(tài)的周期數(shù)并不是成倍數(shù)變化關(guān)系。結(jié)果還顯示，地基的剪切剛度對(duì)系統(tǒng)的概周期運(yùn)動(dòng)和混沌運(yùn)動(dòng)有抑制作用，隨著地基剪切剛度的增大，在激勵(lì)頻率參數(shù)區(qū)域內(nèi)系統(tǒng)的概周期和混沌運(yùn)動(dòng)窗口逐漸減小;當(dāng)?shù)鼗羟袆偠茸銐虼髸r(shí)，系統(tǒng)將始終處于周期運(yùn)動(dòng)狀態(tài)。

［1］Pa?doussis M P. Fluid-structure interactions:slender structures and axial flow，vol.1［M］.London，Academic Press，1998.

［2］Pa?doussis M P，Semler C.Nonlinear and chaotic oscillations of a constrained cantilevered pipe conveying fluid:A full nonlinear analysis［J］.Nonlinear Dynamics，1993，4:655-670.

［3］黃玉盈，鄒時(shí)智，錢 勤，等.輸液管的非線性振動(dòng)、分叉與混沌——現(xiàn)狀與展望［J］.力學(xué)進(jìn)展，1998，28(1):30-42.HUANG Yu-Ying，ZOU Shi-zhi，Qian Qin，et al.Advances and trends of nonlinear dynamics of pipes conveying fluid［J］.Advances in Mechanics，1998，28(1):30-42.

［4］徐 鑒，楊前彪.輸液管模型及其非線性動(dòng)力學(xué)近期研究進(jìn)展［J］.力學(xué)進(jìn)展，2004，34(2):182-194.XU Jian，YANG Qian-biao.Recent development on models and nonlinear dynamics of pipes conveying fluid［J］.Advances in Mechanics，2004，34(2):182-194.

［5］金基鐸，楊曉東，張宇飛.固定約束松動(dòng)對(duì)輸流管道穩(wěn)定性和臨界流速的影響［J］.振動(dòng)與沖擊，2009，28(6):95-99.JIN Ji-duo，YANG Xiao-dong，ZHANG Yu-fei.Analysis of critical flow velocities of pipe conveying fluid under relaxation of boundary conditions［J］.Journal of Vibration and Shock，2009，28(6):95-99.

［6］包日東，金志浩，聞邦椿.一般支承條件下輸流管道的非線性動(dòng)力學(xué)特性研究［J］.振動(dòng)與沖擊，2009，28(7):153-157.BAO Ri-dong，JIN Zhi-hao，WEN Bang-chun.Nonlinear dynamic characteristics of a fluid conveying pipe under condition of commonly elastic supports［J］.Journal of Vibration and Shock，2009，28(7):153-157.

［7］孟 丹，郭海燕，徐思朋.輸流管道的流體誘發(fā)振動(dòng)穩(wěn)定性分析［J］.振動(dòng)與沖擊，2010，29(6):80-83.MENG Dan，GUO Hai-yan，XU Si-peng.Stability analysis on flow-induced vibration of fluid-conveying pipes［J］.Journal of Vibration and Shock，2010，29(6):80-83.

［8］郭長(zhǎng)青，劉紅濤，王曉鋒，等.輸流管道在分布隨從力作用下的振動(dòng)和穩(wěn)定性［J］.工程力學(xué)，2010，27(4):190-196.GUO Chang-qing，LIU Hong-tao，WANG Xiao-feng，et al.Vibration and stability ofpipes conveying fluid with distributed follower force［J］.Engineering Mechanics，2010，27(4):190-196.

［9］黃慧春，張艷雷，陳立群.超臨界條件下固支邊界輸液管的內(nèi)共振［J］.力學(xué)季刊，2011，32(1):48-52.HUANG Hui-chun， ZHANG Yan-lei， CHEN Li-qun.Resonance of clamped-clamped pipes conveying fluid in supercritical range［J］.Chinese Quarterly of Mechanics，2011，32(1):48-52.

［10］Qiao N，Yuying H.Differential quadrature method to stability analysis of pipes conveying fluid with spring support［J］.Acta Mechanica Solida Sinica，2000，13:320-327.

［11］Wang L.A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid［J］.International Journal of Non-Linear Mechanics，2009，44:115-121.

［12］Chellapilla K R，Simha H S.Critical velocity of fluidconveying pipes resting on two-parameter foundation［J］.Journal of Sound and Vibration，2007，302:387-397.

［13］Lottati I，Kornecki A.The effect of an elastic foundation and of dissipative forces on the stability of fluid-conveying pipes［J］.Journal of Sound and Vibration，1986，109:327-338.

［14］Dermendjian-Ivanova D S.Critical flow velocities of a simply supported pipeline on an elastic foundation［J］.Journal of Sound and Vibration，1992，157(2):370-374.

［15］Dutta SC，Roy R.A critical review on idealization and modeling for interaction among soil-foundation-structure system［J］.Computers and Structures，2002，80(20-21):1579-1594.

［16］王忠民，馮振宇，趙鳳群，等.彈性地基輸流管道的耦合模態(tài)顫振分析［J］.應(yīng)用數(shù)學(xué)與力學(xué)，2000，21(10):1060-1068.WANG Zhong-min，F(xiàn)ENG Zhen-yu，ZHAO Feng-qun，et al.Analysis of coupled-mode flutter of pipes conveying fluid on elastic foundation［J］.Applied Mathematics and Mechanics，2000，21(10):1060-1068.

［17］Doared O，de Langre E.Local and global instability of fluidconveying pipes on elastic foundation［J］.Journal of Fluids and Structures，2002，16(1):1-14.

［18］Qian Q，Wang L，Ni Q.Nonlinear response of a fluidconveying pipe embedded in nonlinear elastic foundations［J］.Acta Mechanica Solida Sinica 2008，21(2):171-176.

［19］梁 峰，金基鐸，楊曉東，等.彈性地基上輸流管道的靜態(tài)和動(dòng)態(tài)穩(wěn)定性研究［J］.工程力學(xué)，2010，27(11):166-171.LIANG Feng，JIN Ji-duo，YANG Xiao-dong，et al.Static and dynamic stabilities of fluid pipes on elastic foundation［J］.Engineering Mechanics，2010，27(11):166-171.