基于長周期地震動記錄的SDOF 體系能量譜探討

陳清軍，袁偉澤

(同濟大學土木工程防災國家重點實驗室，上海 200092)

隨著現代文明的進步和社會經濟的飛速發展，建筑物日益向超高層、超大型方向發展，地震動長周期成分對其影響變得不容忽視。如何客觀合理地估計這種影響，現行的設計反應譜和振型分解反應譜方法顯得力不從心。為解決這一難題，許多學者認為可采用更加合理的物理量來描述地震動，并把它應用到工程抗震計算中去，其中地震動能量是可選物理量之一［1］。但是如何將能量方法與結構地震反應，是迄今未能很好解決的問題。

基于能量的抗震設計方法，由于考慮了地震動持時對結構累積損傷的影響，能夠更全面地反映地震作用的特性及其對結構的影響，受到了國內外學者的重視。Akiyama［2］對4種場地的地震動進行分析，提出了兩段式的輸入能量譜;Benavent-Climent等［3］采用哥倫比亞地震記錄建立了適用于中、高地震活躍區的設計輸入能量譜;Amiri等［4］利用伊朗強震記錄建立了彈性輸入能量譜。在國內，滕軍等［5］分析了160條強震記錄，建議了簡化三段式能量譜曲線;程光煜等［6］以4種場地條件下40條強震記錄作為輸入，分析了彈塑性SDOF系統的地震輸入能量譜，并對地震動強度和SDOF系統參數對地震輸入能量譜的影響進行了研究。由于受強震觀測儀器等因素影響，具有可靠長周期信息的地震動記錄比較缺乏［7］，至今國內外有關地震動能量譜的研究大多是基于普通周期地震動記錄，而關于長周期地震動能量譜的研究成果仍較少。

為分析長周期地震動作用下結構的能量反應譜及其影響因素，本文將從1985年墨西哥8.1級地震、1999年臺灣集集7.6級地震和2003年日本十勝沖8.0級地震記錄庫中，挑選出具有可靠長周期信息和基本場地資料的強震記錄作為輸入，分析長周期地震動彈性輸入能量譜的特點，探討長周期地震動彈塑性輸入能量譜的影響因素及其確定方法、以及長周期地震動作用下結構的累積滯回耗能與彈塑性輸入能量之間的比值關系。

1 能量法基本理論概述

基底受水平地震動作用的單自由度(SDOF)阻尼體系的運動方程可寫成為:

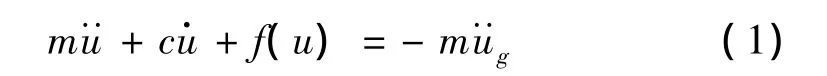
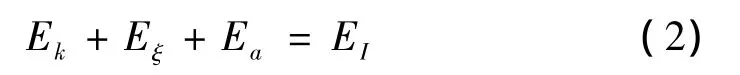
對于彈性SDOF系統，式(2)中累積滯回耗能Eh為零，地震結束時，結構的動能Ek和彈性變形能Es幾乎為零，因此，結構的耗能能力主要取決于阻尼耗能Eξ;對于彈塑性SDOF系統，結構的耗能能力主要取決于累積滯回耗能Eh和阻尼耗能Eξ。若由Ek和Es構成彈塑性體系中的彈性振動能Ee，則式(2)可表示為:

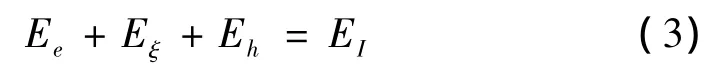
地震作用結束時，式(3)中的彈性振動能Ee幾乎為零，則累積滯回耗能Eh=EI-Eξ。已有的研究表明［2-3，6］，延性系數μ和阻尼比ξ是地震動輸入能量和結構累積滯回耗能的主要影響因素。取一系列自振周期為Ti(i=1，2，…，N)的SDOF體系，則在地震動g作用下，結構最大輸入能量響應和滯回耗能響應可分別表示為因此，設定結構的阻尼比和延性系數后，采用逐步積分法(本文計算時采用Newmark-β法)，通過迭代計算確定結構的屈服位移，就可獲得在指定阻尼比情形下，與目標延性系數一致的地震動輸入能量譜和累積滯回耗能譜。

若式(1)中各項對絕對位移(u+ug)在地震動持時內積分，可以得到絕對能量平衡方程。絕對輸入能量與相對輸入能量的不同，主要是由于結構體系的剛體轉換作用造成的，雖然絕對輸入能量的物理意義較明確，但它包含了作等速運動時與變形無關的能量，對抗震設計意義不明顯［8］。另外，相對能量平衡方程和絕對能量平衡方程關于累積滯回耗能的定義也完全相同，因此，與大部分學者［2，6］選擇能量平衡方程類似，本文將采用相對能量平衡方程對長周期地震動作用下的輸入能量譜和累積滯回耗能譜進行研究。

2 長周期地震動記錄的選取

本文從1985年墨西哥8.1級地震、1999年臺灣集集7.6級地震和2003年日本十勝沖8.0級地震記錄庫中，挑選出具有可靠長周期信息和具有基本場地資料的36條地震加速度水平分量記錄。所有加速度記錄峰值均大于30 gal，對于存在基線漂移的地震記錄采用文獻［9］的方法進行處理。由于收集到的記錄均為境外強震記錄，臺站場地資料不夠完善，而且國內和境外的場地土分類標準也不一樣，不能完全按照我國規范中的場地分類標準來劃分場地類別，因此參考文獻［10］的方法將場地劃分為基巖場地、一般場地和軟土場地三類。按照場地條件的不同，表1給出了所選長周期地震動記錄的主要參數，包括峰值加速度(PGA)、峰值速度(PGV)、峰值位移(PGD)、強震持時(tD)、累積絕對速度

3 能量譜歸一化方法的確定

為了獲得設計用的能量譜，需要將不同幅值地震動的能量譜進行歸一化處理。目前常用的方法主要有:①在能量反應分析之前，通過調整輸入地震動的參數(如PGA、PGV等)進行歸一化。該方法雖然比較簡單，但不能考慮震級、震中距等因素的影響;②利用考慮震級、震中距等因素的能量反應譜參數對反應譜進行歸一化，如能量反應譜的峰值EImax、能量反應譜的面積 AEⅠ。

Decanini等［12］的研究表明，能量譜峰值參數EImax通常對應的頻帶較窄，當周期范圍較大時，該參數不具代表性，且在能量譜的統計分析過程中會導致較大的誤差;而由能量反應譜面積AEⅠ歸一化的能量譜曲線更加平滑，且計算周期范圍較大，統計結果較穩定。因此，本文將采用能量反應譜面積AEⅠ對能量反應譜進行歸一化處理。

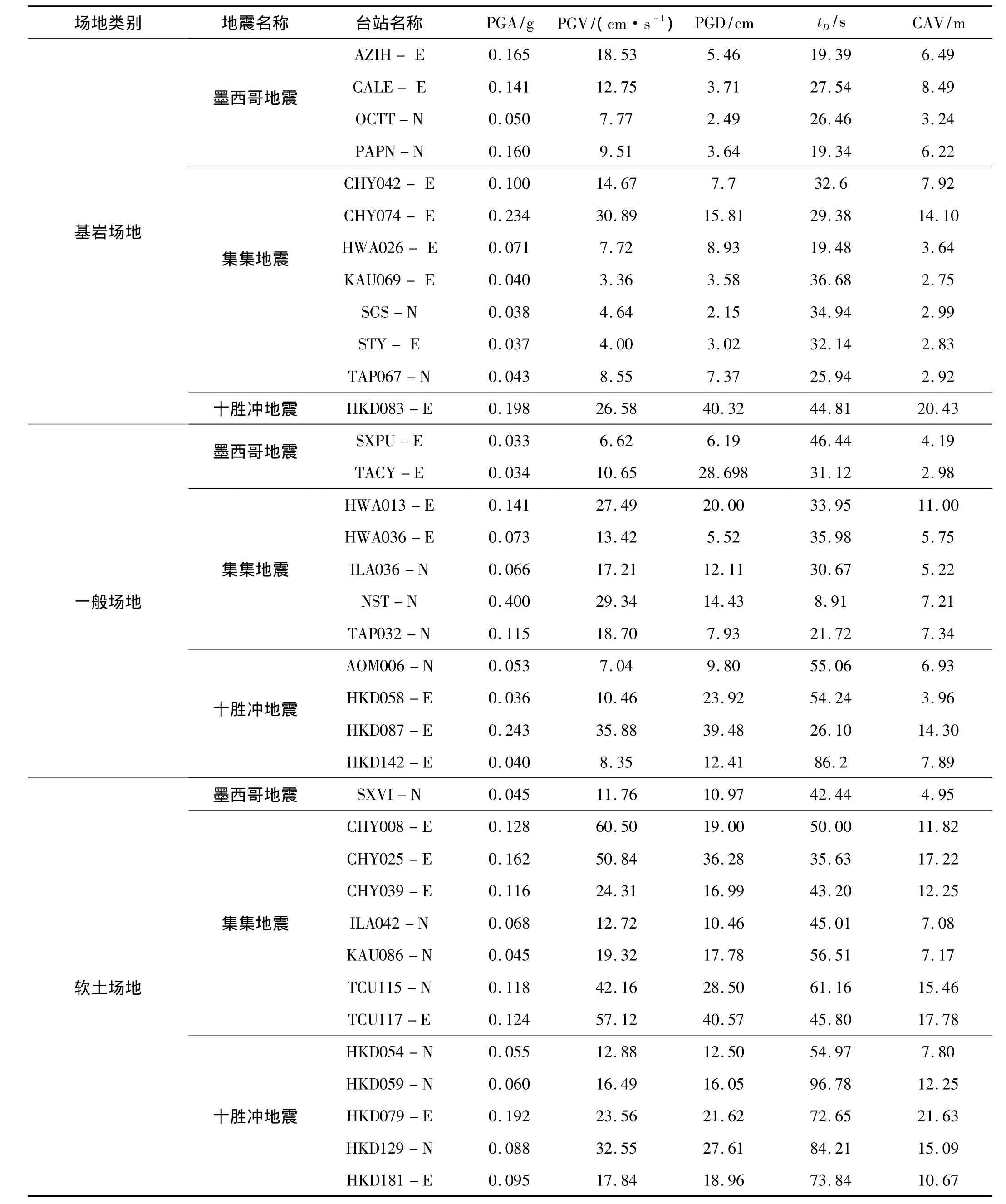
表1 選取的長周期地震動記錄及其地震動參數Tab.1 Chosen long-period ground records and some of their characteristics

4 基于長周期地震動記錄的能量譜

目前已有的設計能量譜多為兩段式和三段式模型。兩段式模型上升段的斜率相同，根據場地條件的不同能量譜的最大值和界限周期有所不同，在界限周期以后能量譜值保持不變［2］，然而地震動能量譜在界限周期以后大小是有變化的，峰值和低谷的值隨著地震動的不同而不同，在長周期范圍能量譜將減小［13］。相比之下，三段式模型更能概括能量譜的統計特征［5］，且可根據場地條件的不同采用不同的能量譜峰值和界限周期，因此，這里將采用三段式能量譜模型進行長周期地震動的能量譜分析。

4.1 彈性能量譜

取阻尼比ξ=0.02，分別以基巖場地、一般場地和軟土場地情形下的長周期地震動作為輸入，對彈性SDOF體系進行輸入能量譜計算，并采用能量譜參數AEⅠ，ξ=0.02進行歸一化處理，得到上述三類場地條件下的標準能量譜曲線和代表值曲線(均值加一倍方差)如圖1所示。

分析圖1基巖場地、一般場地和軟土場地中的能量譜代表值曲線可知，能量譜曲線可分為上升段、平臺段和下降段3段。在短周期范圍內，能量譜值隨周期增加而加大;在中等周期范圍內，能量譜值在一定量值附近震蕩，上下變化不大，此段的長度隨土質變軟，呈變長趨勢;在長周期范圍內，能量譜值隨周期增長而下降。參照文獻［5］和［6］的方法，引入如下形式擬合函數:

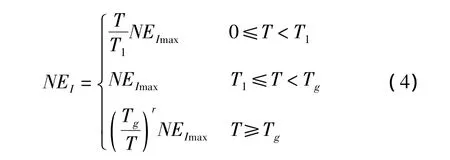
式中:NEImax為阻尼比ξ=0.02時的能量譜平臺段譜值，T1和Tg分別為能量譜平臺段的起始和結束周期，r為能量譜下降段的衰減指數。

分別對三類場地的能量譜代表值曲線應用最小二乘法進行擬合，即令:

圖1 三類不同場地的地震動輸入能量譜Fig.1 Input energy spectrum of different soil types

表2 擬合彈性能量譜參數Tab.2 Factors for fitted input energy spectrum

當阻尼比ξ≠0.02時，需要對能量譜進行修正，參考現行抗震設計規范中不同阻尼比的設計反應譜形式，通過對不同阻尼比情形下三種場地的長周期地震動能量譜的統計分析，得到彈性能量譜平臺段的幅值調整系數η2和曲線下降段衰減指數r'的計算式為:

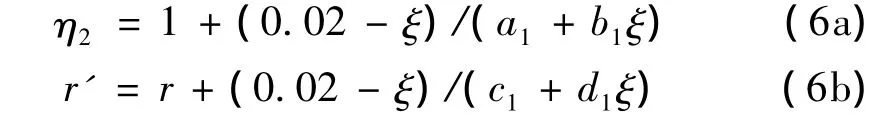
其中參數 a1，b1，c1，d1的取值見表 3。

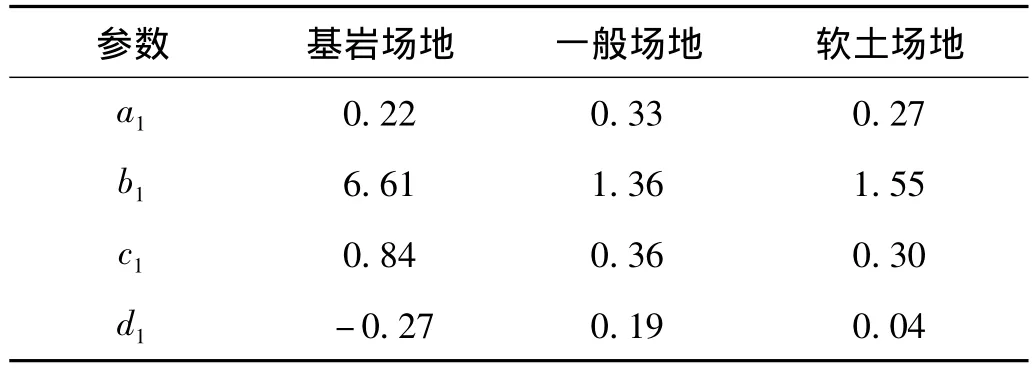
表3 能量譜調整參數Tab.3 Adjustment factors of input energy spectrum

4.2 彈塑性能量譜及其影響因素

鑒于雙線性恢復力模型具有形式簡單、計算方便同時又能反映結構彈塑性滯回本質的特點，這里將采用理想雙線性模型進行彈塑性計算，首先討論延性系數和阻尼比對能量譜值、以及能量譜峰值的影響;然后，參考文獻［6］的方法，調整長周期地震動彈性能量譜參數來確定長周期地震動的彈塑性能量譜，并通過與長周期地震動彈塑性能量譜擬合結果的比較，來驗證這一方法的可行性。

4.2.1 延性系數和阻尼比對能量譜值的影響

首先以阻尼比ξ=0.02為例，討論阻尼比一定時延性系數對彈塑性能量譜與彈性能量譜比值EI，ξ=0.02，μ/EI，ξ=0.02，μ=1的影響。圖 2 給出了取不同延性系數時彈塑性能量譜與彈性能量譜的比值 EI，ξ=0.02，μ/EI，ξ=0.02，μ=1隨 SDOF 體系初始周期的變化曲線。由此可見，在短周期范圍內，彈塑性能量譜的譜值明顯大于彈性能量譜，且隨著延性系數的增大，彈塑性能量譜的譜值變大趨勢越明顯;在中、長周期范圍內，延性系數對彈塑性能量譜譜值的影響減弱，能量譜比值趨于平緩，同時隨著結構非線性的增強，彈塑性能量譜與彈性能量譜的比值有減小趨勢。

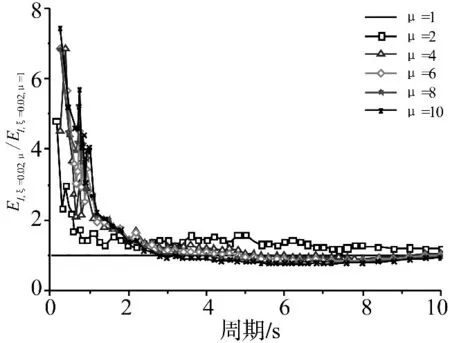
圖2 延性系數對彈塑性能量譜的影響Fig.2 Influence of ductility factor on elastic-plastic energy spectrum

經過對計算結果的統計分析與擬合，可得到不同延性系數μ時，彈塑性能量譜與彈性能量譜比值R1的擬合公式:

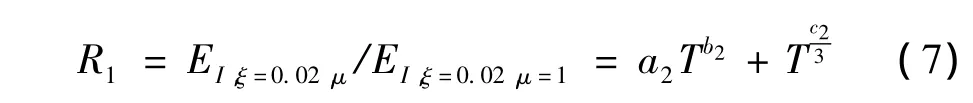
式中:T為SDOF體系的自振周期;參數a2，b2，c2由下面的公式確定:

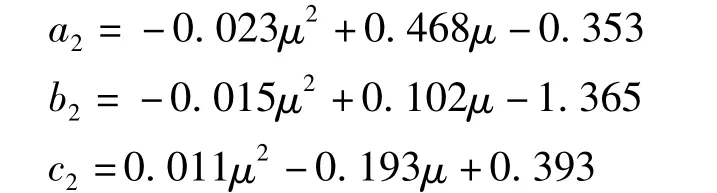
進一步討論延性系數一定時，阻尼比對地震動能量譜的影響。以延性系數μ=4的彈塑性SDOF體系為例，圖 3 給出了不同阻尼比 ξ的能量譜值 EI，ξ，μ=4與阻尼比 ξ=0.02 時的能量譜值 EI，ξ=0.02，μ=4隨 SDOF 體系初始周期的變化曲線。由圖3可知:①當周期值小于1.2 s時，彈塑性能量譜的譜值隨周期的增大而減小，且阻尼比ξ越大，彈塑性能量譜減小的趨勢越明顯;②當周期值大于1.2 s時，彈塑性能量譜的譜值隨周期的增大而增大，且阻尼比ξ越大，彈塑性能量譜增大的趨勢越明顯。

經過對計算結果的統計分析與擬合，可得到不同阻尼比ξ時彈塑性能量譜與彈性能量譜比值R2的擬合公式:

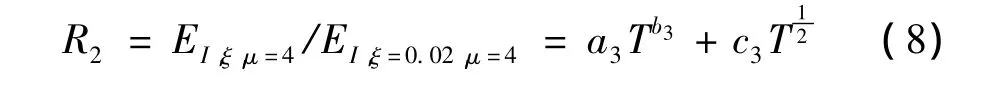
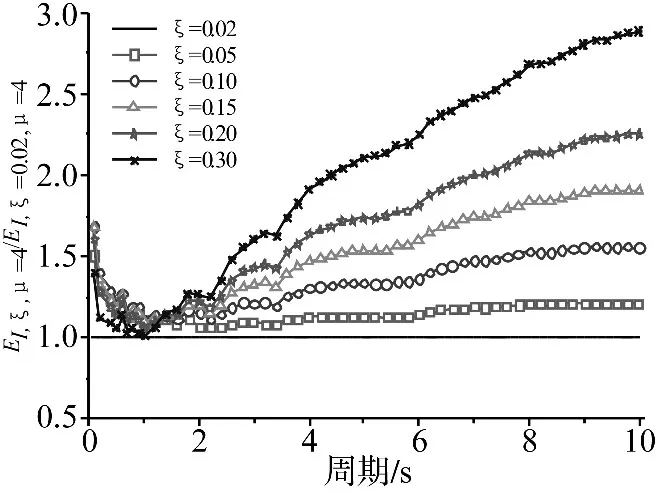
圖3 阻尼比對彈塑性能量譜的影響Fig.3 Influence of damping ratio on elastic-plastic energy spectrum

式中:T為SDOF體系的自振周期;參數a3，b3，c3由下面的公式確定:

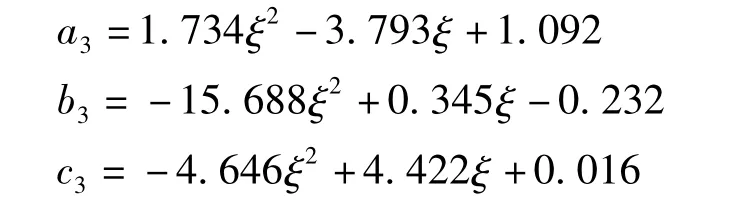
綜合上述分析結果，可得到不同延性系數和阻尼比的彈塑性體系能量譜值 EI，ξ，μ，與阻尼比為 0.02 的彈性體 系 能 量 譜 值 EI，ξ=0.02，μ=1之 間 的 比 值 ET，ξ，μ關 系式，即:

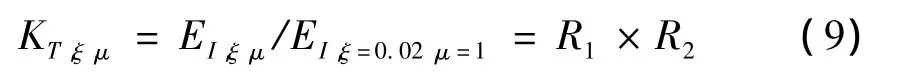
4.2.2 延性系數和阻尼比對能量譜峰值的影響

為分析延性系數μ和阻尼比ξ對長周期地震動能量譜峰值的影響，這里將不同延性系數和阻尼比的彈塑性能量譜的峰值 EImax，ξ，μ與阻尼比為 0.02 的彈性能量譜的峰值 EImax，ξ=0.02，μ=1進行比較分析。以表 1 選取的36條長周期地震動作為輸入，求得彈塑性能量譜峰值與彈性能量譜峰值的比值 EImax，ξ，μ/EImax，ξ=0.02，μ=1的均值加一倍方差結果如圖4所示。

由圖4可知，在相同阻尼比的情形下，彈塑性能量譜峰值與彈性能量譜峰值的比值 EImax，ξ，μ/EImax，ξ=0.02，μ=1隨延性系數μ的增大而呈減小趨勢;當阻尼比ξ增大時，延性系數對能量譜峰值的影響呈減弱趨勢。

通過對計算結果的統計分析與擬合，可得到不同阻尼比和延性系數的彈塑性能量譜峰值與阻尼比ξ=0.02的彈性能量譜峰值之間比值β的關系式為:

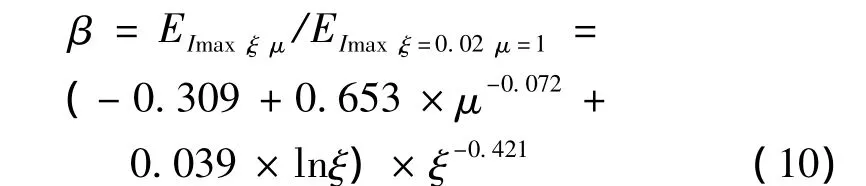
4.2.3 彈塑性能量譜

［6］的方法，利用4.1節建立的長周期地震動彈性能量譜，通過調整公式(4)中的參數來確定長周期地震動彈塑性能量譜。具體如下:①彈塑性能量譜平臺段的譜值 NEImax，ξ，μ= β × NEImax，其中系數 β 可由公式(10)計算得到;②對周期T≥Tg之后的長周期段能量譜值乘以調整系數 γ，其中 γ =KT，ξ，μ/KTg，ξ，μ可通過公式(9)求得。利用上述方法求得的基于長周期地震動彈性能量譜的彈塑性能量譜曲線見圖5。

為驗證上述方法的可行性，以表1中三種場地條件下的長周期地震動作為輸入，對SDOF體系進行彈塑性時程響應計算，求取不同延性系數和阻尼比情形下由能量譜面積AEI歸一化的標準彈塑性能量譜曲線，并與基于長周期地震動彈性能量譜的彈塑性能量譜曲線進行對比。圖5給出了基巖場地(ξ=0.02，μ=1)、一般場地(ξ=0.05，μ =4)和軟土場地(ξ=0.10，μ =6)三種情況下，標準彈塑性能量譜曲線及其代表值曲線(均值加一倍方差)、以及擬合值曲線(通過公式(5)獲得)，與基于長周期地震動彈性能量譜的彈塑性能量譜曲線的比較。由此可見，基于長周期地震動彈性能量譜的彈塑性能量譜曲線與基于實測長周期地震動的彈塑性能量譜的擬合值曲線基本吻合，兩者平臺段的譜值相差約5%。

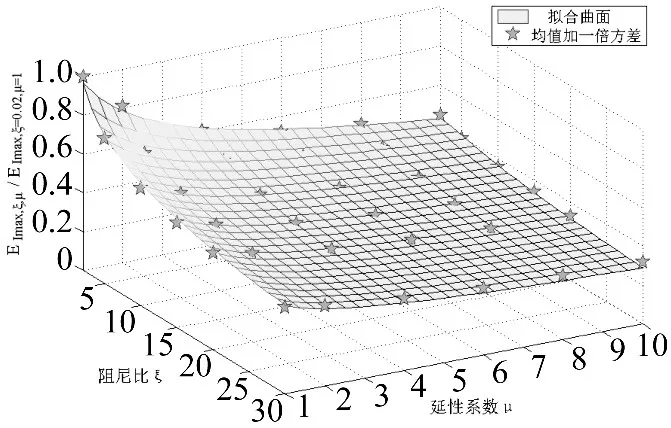
圖4 能量譜峰值擬合曲面Fig.4 Fitting surface for the peak value of energy spectrum

圖5 不同延性系數和阻尼比情況下彈塑性能量譜對比Fig.5 Comparison of elastic-plastic energy spectrum based on different ductility factors and damping ratios

4.3 累積滯回耗能譜

地震作用下結構的累積損傷主要取決于累積滯回耗能，累積滯回耗能是對結構進行非線性設計、或對結構進行地震危險性評估的一個主要參數。在確定地震動彈塑性輸入能量譜的基礎上，通過分析累積滯回耗能Eh與地震輸入能量EI的比值譜Eh/EI(以下簡稱滯回耗能比值譜)來分析累積滯回耗能Eh隨結構周期的變化情況。

將SDOF體系在不同阻尼比(以 ξ=0.02和 ξ=0.20為例)和延性系數下的滯回耗能比值譜隨周期的變化情況進行比較，如圖6所示。

圖6 阻尼比和延性系數對滯回耗能比值的影響Fig.6 Influence of damping ratios and ductility factors on hysteretic energy radio

由圖6可知:①滯回耗能的比值隨結構自振周期的增大，逐漸減小，并且延性系數越大，減小的趨勢越明顯;②當延性系數一定時，阻尼比越大，結構的滯回耗能比值越小;③當阻尼比一定時，延性系數越大，滯回耗能的比值越高。

若以結構自振周期為一定值(這里取周期為4 s)，延性系數對滯回耗能比值Eh/EI的影響曲線如圖7所示。由此可見，當延性系數μ小于4時，延性系數對滯回耗能比值的影響明顯;當延性系數μ大于4時，延性系數對滯回耗能比值的影響減弱。

圖7 延性系數對滯回耗能比值的影響Fig.7 Influence of ductility factor on hysteretic energy radio

目前關于滯回耗能比值譜的計算模型主要有:考慮阻尼影響的Akiyama模型［2］、考慮延性系數的Fajfar模型［14］、考慮阻尼比和延性系數的Benavent-Climent模型［3］和 Decanini模型［12］。這些模型大都沒有考慮周期因素對滯回耗能比值譜的影響，綜合統計分析結果，并參考文獻［15］的形式，可得到長周期地震動滯回耗能比值譜的關系式為:

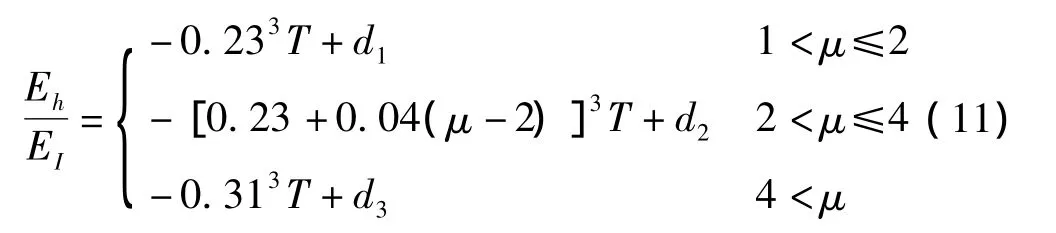
式中:d1=5.34ξ2-3.05ξ+0.65，

d2=d1+(d3-d1)(μ -2)/2，

d3=5.57ξ2-3.62ξ+0.95。

將已有模型與公式(11)的計算結果進行比較，若采用一般場地、阻尼比 ξ=0.05、延性系數 μ=4的SDOF體系，各模型計算結果與長周期地震動彈塑性時程計算結果的對比如圖8所示。由圖8可知，除Decanini模型外，其他模型均未考慮周期的影響，因此在整個周期范圍內為一條直線。其中Akiyama模型在短周期范圍內與時程計算結果較接近，但在長周期段的比值偏高;Fajfar模型在整個周期范圍內的比值均偏高;Decanini模型雖然考慮了周期的影響，但結構周期只計算到4 s，同時該模型的計算結果偏低;Benavent-Climent模型計算的比值大于1，不能滿足邊界條件，表明該模型已超出了適應范圍;公式(11)同時考慮了周期、阻尼比和延性系數的影響，其分析結果與長周期地震動彈塑性時程計算結果(均值加一倍方差)接近。

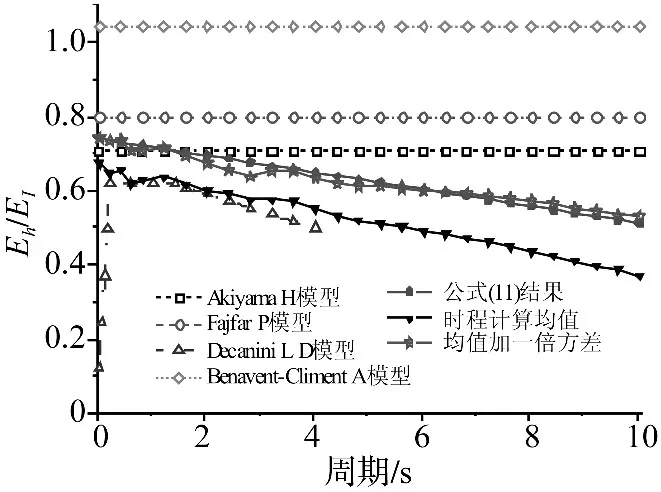
圖8 計算結果比較Fig.8 Comparison of the calculation results

5 結論

本文選取36條具有可靠長周期信息的強震記錄作為輸入，采用能量譜面積進行歸一化，分析了長周期地震動作用下結構的能量反應譜及其影響因素。結果表明:

(1)長周期地震動的彈性能量譜曲線可以分為三段，即上升段、平臺段和下降段，且場地土的土質越軟，平臺段越長;本文建立的彈性能量譜模型能夠較好地擬合周期在10 s以內、阻尼比在0.02～0.30內的長周期能量譜的統計特征。

(2)與彈性能量譜相比，彈塑性能量譜在短周期范圍，隨延性系數的增大能量譜值增大顯著，在中、長周期范圍，隨著延性系數增大，能量譜值略有減小;而阻尼比對能量譜的影響與延性系數相反。本文通過調整長周期地震動彈性能量譜參數確定的長周期地震動彈塑性能量譜，與長周期地震動彈塑性能量譜的擬合結果基本吻合，兩者平臺段的譜值相差5%左右。

(3)本文建立的長周期地震動累積滯回耗能比值譜計算公式，考慮了結構的延性系數、阻尼比和自振周期的影響，所得結果與彈塑性時程計算結果(均值加一倍方差)接近。

需要指出的是，由于此次選取的長周期地震動記錄相對有限，針對長周期地震動能量譜模型的相關參數有待更多實測長周期地震動記錄加以驗證。

參考文獻

［1］王亞勇.關于設計反應譜、時程法和能量方法的探討［J］.建筑結構學報，2000，21(1):21-28.WANG Ya-yong.A review of seismic response spectra，time history analysis and energy method［J］.Journal of Building Structures，2000，21(1):21-28.

［2］Akiyama H.Earthquake resistant limit state design for buildings［M］.University of Tokyo Press，1985.

［3］Benavent-Climent A，Lopez-Almansa F，Bravo-Gonzalez D A.Design energy input spectra for moderate-to-high seismicity regions based on Colombian earthquakes［J］.Soil Dynamics and Earthquake Engineering，2010，30:1129-1148.

［4］Amiri G G，Darzi G A，Amiri J V.Design elastic input energy spectra based on Iranian earthquakes［J］.Canadian Journal of Civil Engineering，2008，35(6):635 646.

［5］Teng J，Dong Z J.Research on energy spectrum of elastic SDOF［C］//The 14th World Conference on Earthquake Engineering.China:Beijing，2008.

［6］程光煜，葉列平.彈塑性SDOF系統的地震輸入能量譜［J］.工程力學，2008，25(2):28-39.CHENG Guang-yu，YE Lie-ping.Earthquake input energy spectrum for inelastic SDOF systems［J］.Engineering Mechanics，2008，25(2):28-39.

［7］李春鋒，張 旸.長周期地震動衰減關系研究的迫切性［J］.地震地磁觀測與研究，2006，27(3):1-8.LI Chun-feng，ZHANG Yang.Urgency of the study of longperiod ground motion［J］.Seismological and Geomagnetic Observation and Research，2006，27(3):1-8.

［8］Uang C M，Bertero V V.Evaluation of seismic energy in structures［J］.EarthquakeEngineeringand Structural Dynamics，1990，19(1):77-99.

［9］胡燦陽，陳清軍.基于EMD和最小二乘法的基線漂移研究［J］.振動與沖擊，2010，29(3):162-167.HU Can-yang，CHEN Qing-jun.Research on baseline drift using least-square and EMD ［J］.Journal of Vibration and Shock，2010，29(3):162-167.

［10］周雍年，周正華，于海英.設計反應譜長周期段的研究［J］.地震工程與工程振動，2004，24(2):15-18.ZHOU Yong-nian，ZHOU Zheng-hua，YU Hai-ying.A study on long period portion of design spectra［J］.Earthquake Engineering and Engineering Vibration，2004，24(2):15-18.

［11］Trifunac M，Brady A.A study on the duration of strong earthquake ground motion［J］.Bulletin of the Seismological Society of America，1975，65(3):581-626.

［12］Decanini L D，Mollaioli F.Formulation of elastic earthquake input energy spectra［J］.Earthquake Engineering and Structural Dynamics，1998，27(12):1503-1522.

［13］Akiyama H.Earthquake-resistant design method for buildings based on energy balance［M］. Gihoudou Syuppan Press，1999.

［14］Fajfar P， Vidic T. Consistentinelastic design spectra hysteretic and input energy［J］.Earthquake Engineering and Structural Dynamics，1994，23(5):523-537.

［15］程光煜，葉列平.彈塑性SDOF系統累積滯洄譜［J］.工程抗震與加固改造，2007，29(2):1-7.CHENG Guang-yu， YE Lie-ping. Cumulativehysteretic energy spectra of SDOF systems［J］.Earthquake Resistant Engineering and Retrofitting，2007，29(2):1-7.