一種局域共振型角式聲子晶體梁

舒海生，郜 冶，張 法，高恩武，李世丹，董立強

(哈爾濱工程大學(xué) 機電工程學(xué)院702所，哈爾濱 150001)

局域共振型聲子晶體能夠?qū)崿F(xiàn)小尺寸控制大波長，在工程減振領(lǐng)域具有十分重要的應(yīng)用前景［1］。很多研究者［2－9］已經(jīng)開展了從一維到三維的局域共振型聲子晶體的研究，這些研究主要是針對不同的局域振子形狀和材料以及不同的振動形式進(jìn)行了分析，取得了很多重要的結(jié)論。在現(xiàn)有的一維聲子晶體件的研究［5－10］中，大多是針對梁進(jìn)行帶隙計算和減振研究，一般只考慮單個方向的激擾，因而事實上是將其作為一維減振結(jié)構(gòu)來分析的。工程實際中的激擾往往是多方向的，往往需要對多個自由度的振動激擾加以隔離或抑制，因此構(gòu)造合理的聲子晶體結(jié)構(gòu)來獲得多維減振性能顯然具有十分重要的實際意義。本文首先通過分析局域共振型聲子晶體梁的帶隙特性和傳遞率曲線，說明了直梁僅具有二維減振能力，因而不能滿足多維減振需求，然后提出了一類角式局域共振型聲子晶體梁結(jié)構(gòu)，并進(jìn)行了傳遞矩陣推導(dǎo)和數(shù)值求解，結(jié)果對比表明了該角式聲子晶體梁能夠通過縱波和橫波之間的波型轉(zhuǎn)化，使得橫向振動帶隙的強衰減和寬頻帶特性得到有效的利用，最終實現(xiàn)了三維減振。

1 局域共振型聲子晶體梁的振動帶隙

梁的單個周期結(jié)構(gòu)如圖1所示，材料參數(shù)如下:

鋁:密度2 799 kgm－3;楊氏模量 7.21e10 Pa;泊松比0.345 1。

硫化橡膠:密度1 300 kgm－3;楊氏模量1e6 Pa;泊松比 0.470 6。

銅:密度8 950 kgm－3;楊氏模量16.46e10 Pa;泊松比0.093。

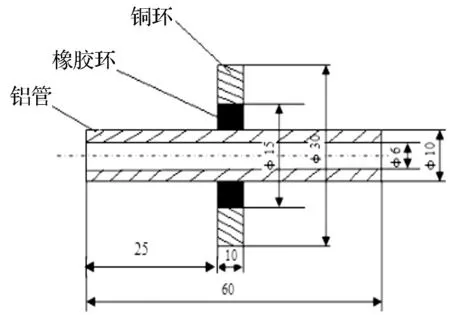
圖1 聲子晶體梁單個周期結(jié)構(gòu)Fig.1 Single period structure of straight beam of phononic crystals

由該周期單元構(gòu)成的無限長聲子晶體梁的縱向振動和橫向振動的傳播特性均可采用傳遞矩陣法分析，結(jié)合周期結(jié)構(gòu)的Bloch定理，即可得到標(biāo)準(zhǔn)特征值問題如下［1］:

其中:T為縱向振動傳遞矩陣或橫向振動傳遞矩陣，I為2×2(縱向)或4×4(橫向)的單位矩陣。

對于給定頻率ω，即可求出相應(yīng)的波矢q，根據(jù)其是否為實數(shù)或復(fù)數(shù)即可得到無限長聲子晶體梁振動波的能帶結(jié)構(gòu)。

對于有限長的聲子晶體梁，為計算其橫向和縱向振動帶隙，有限元方法是十分方便的。為此，將所建立的如圖2所示的5周期梁模型導(dǎo)入到Ansys/workbench中進(jìn)行諧響應(yīng)分析，分別在梁的一端加載軸向和橫向諧位移激勵，在另一端測量相應(yīng)的位移信號，經(jīng)計算獲得了如圖3、4所示的縱向振動傳遞率曲線和橫向振動傳遞率曲線。

圖2 聲子晶體梁三維模型Fig.2 3 － Dimensional model of straight beam of phononic crystals

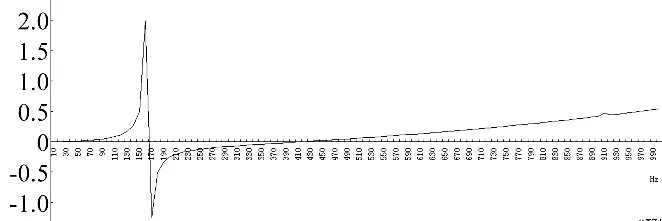
圖3 聲子晶體梁的縱向振動傳遞率Fig.3 Longitudinal vibration transmissibility of straight beam of phononic crystals

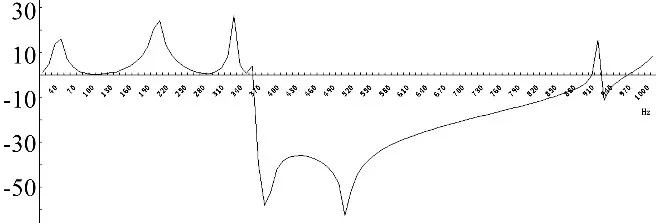
圖4 聲子晶體梁的橫向振動傳遞率Fig.4 Transverse vibration transmissibility of straight beam of phononic crystals

很明顯，在0～1 000 Hz范圍內(nèi)，梁的縱向振動帶隙出現(xiàn)在170～180 Hz這個很窄的頻帶，且該范圍內(nèi)的衰減極為有限，僅為－1 dB左右。對橫向振動而言，該梁的帶隙出現(xiàn)在360～900 Hz，頻帶較寬，衰減很強，一般在－20 dB以上，因而該橫向帶隙具有較好的工程減振能力。

事實上，采用此類聲子晶體梁作為結(jié)構(gòu)件或隔振件時，只能實現(xiàn)二維減振(此處只考慮平動自由度)，即垂直于梁軸線的平面內(nèi)的兩個正交方向的橫向振動可以在同一頻帶(此處即為360～900 Hz)得到有力的抑制，而沿著梁軸線方向的縱向振動卻很難在同一頻帶內(nèi)也獲得有效的衰減，其主要原因一方面在于基體梁的縱向剛度遠(yuǎn)大于橫向剛度，因而縱向帶隙衰減量一般遠(yuǎn)小于橫向帶隙衰減量，另一方面在于局域振子設(shè)計時的縱振固有頻率和橫振固有頻率也往往很難調(diào)整到同一區(qū)間。工程中的外界激擾往往是多方向的，既有橫向激擾分量，也有縱向激擾分量，因此使用梁進(jìn)行振動抑制往往不能有效地滿足實際多維減振需求。

2 角式聲子晶體梁的振動傳遞矩陣分析

圖5給出了角式聲子晶體梁模型，該模型由兩段聲子晶體梁組成，上梁與下梁呈固定夾角布置。當(dāng)下梁內(nèi)傳播的縱波到達(dá)兩梁交匯點時，將被部分轉(zhuǎn)化為相應(yīng)頻率的橫波，并在上梁內(nèi)繼續(xù)傳播到遠(yuǎn)端;反之，下梁內(nèi)的橫波前進(jìn)到交匯點時也將被部分轉(zhuǎn)化為相應(yīng)頻率的縱波，并在上梁內(nèi)繼續(xù)傳播。顯然，從下梁自由端進(jìn)入的任意方向的外界激擾將不可避免地形成上梁或下梁的橫向振動，因此可以預(yù)見具有很強振動抑制能力的橫向帶隙必定能夠發(fā)揮其作用，從而將減振能力從二維拓展到三維。

對下梁(梁1)，將坐標(biāo)系原點選在自由端時，面內(nèi)橫向振動和縱向振動的傳遞關(guān)系可以表示為:

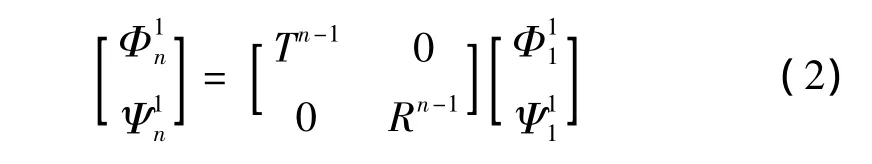
其中:T、R分別為對應(yīng)聲子晶體直梁的橫振和縱振傳遞矩陣，n為周期數(shù)，、分別為梁1起止周期段上的橫振解的振型函數(shù)系數(shù)列陣(4×1)，、分別為梁1起止周期段上的縱振解的振型函數(shù)系數(shù)列陣(2×1)。

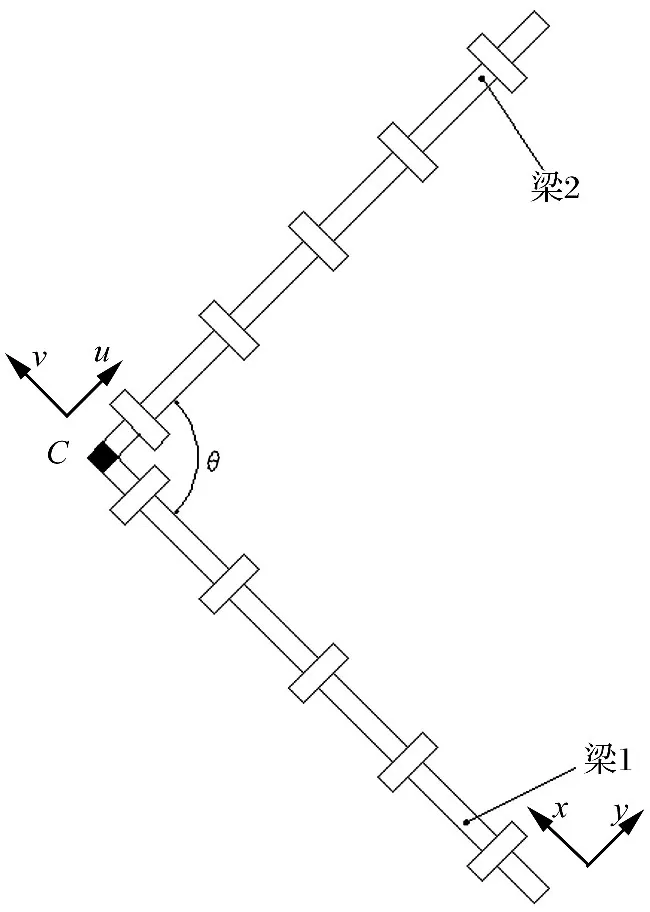
圖5 角式局域共振型聲子晶體梁Fig.5 Locally resonant angle type beam of phononic crystals

類似地，將坐標(biāo)系原點選在交叉點C處時，對上梁(梁2)也存在下述傳遞關(guān)系(此處的上下梁設(shè)為相同結(jié)構(gòu)):

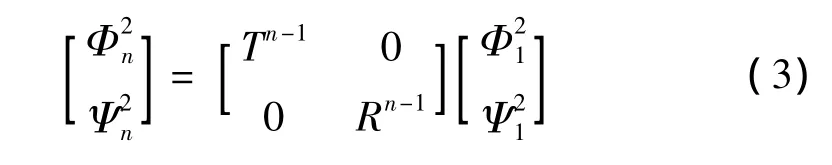
在交叉點C處應(yīng)滿足以下協(xié)調(diào)方程:

(1)位移協(xié)調(diào)條件:

(2)轉(zhuǎn)角協(xié)調(diào)條件:

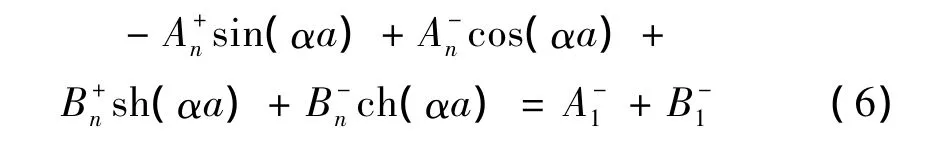
(3)應(yīng)力協(xié)調(diào)條件:

其中:a為周期長度，A為梁的橫截面積。

(4)彎矩協(xié)調(diào)條件:

協(xié)調(diào)方程(4)～(9)可簡寫為矩陣式KΦn=KΦ1，其中:

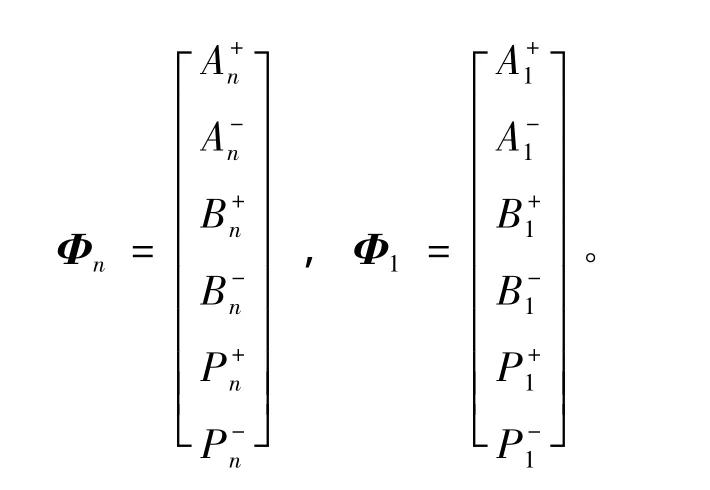
限于篇幅，此處不再列出K和H。

由此可得到兩梁在交叉點處的傳遞關(guān)系:

其中波型轉(zhuǎn)化矩陣Γ=H－1K。

聯(lián)立式(2)、(3)、(10)可得:

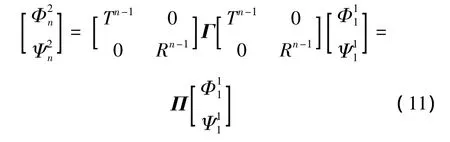
其中:角梁的總傳遞矩陣為:

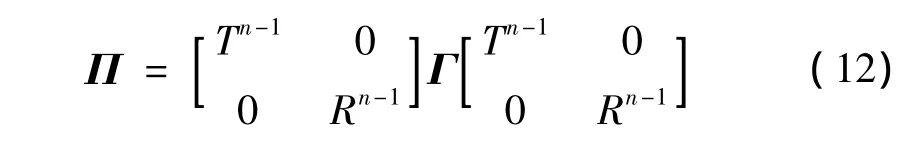
式(12)給出了該角式聲子晶體梁兩端彈性波(包括縱波和橫波)輸出與輸入之間的傳遞轉(zhuǎn)換關(guān)系。

針對 θ=60°、90°、120°三種不同夾角情況采用matlab軟件進(jìn)行了數(shù)值計算。在橡膠環(huán)的徑向和軸向剛度的確定時，由于文獻(xiàn)［1］中所給出的橡膠等效徑向剛度計算公式為近似計算，當(dāng)橡膠環(huán)寬度較大時，誤差較大，此外該公式也不能用于計算軸向剛度，因而此處采用了Ansys靜力學(xué)計算方法來確定，其中徑向剛度為:k1=2.611 5 ×105N/m，軸向剛度為:k2=5.288 5×105N/m。

圖6～圖11給出了角梁在豎直和水平方向的傳遞率分析結(jié)果，不難看出θ=60°時角梁只對豎直方向有明顯的減振效果，而對水平方向的減振效果很弱;θ=120°時角梁只對水平方向有明顯的減振效果，而對豎直方向的減振效果很弱，而θ=90°的角梁對豎直和水平兩個方向綜合減振效果最好，除去550 Hz和850 Hz的共振峰，在360～530 Hz，570～840 Hz，870～950 Hz不論在豎直和水平方向均具有較強的振動衰減。事實上該結(jié)果也是容易理解的，這是因為在非直角情況下，上下梁之間的波型轉(zhuǎn)換是不充分的，因而橫向帶隙的強衰減作用總是偏向于豎直方向(銳角時)或水平方向(鈍角時)，從極限角度(0°和180°)情況也不難體會到這一點。為此，在后面的Ansys分析中將進(jìn)一步著重考察θ=90°的角梁。

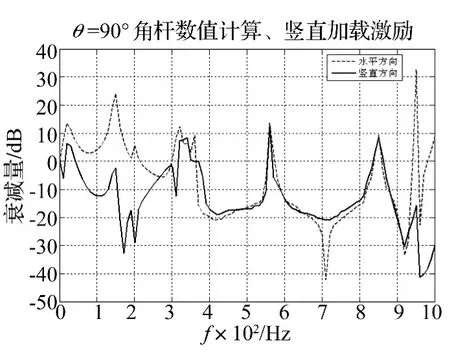
圖6 加載豎直位移激勵時90°角梁的傳遞率Fig.6 Transmissibility of right-angle type beam being loaded vertical displacement excitation

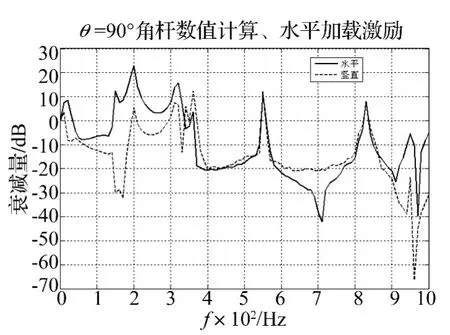
圖7 加載水平位移激勵時90°角梁的傳遞率Fig.7 Transmissibility of right-angle type beam being loaded horizontal displacement excitation

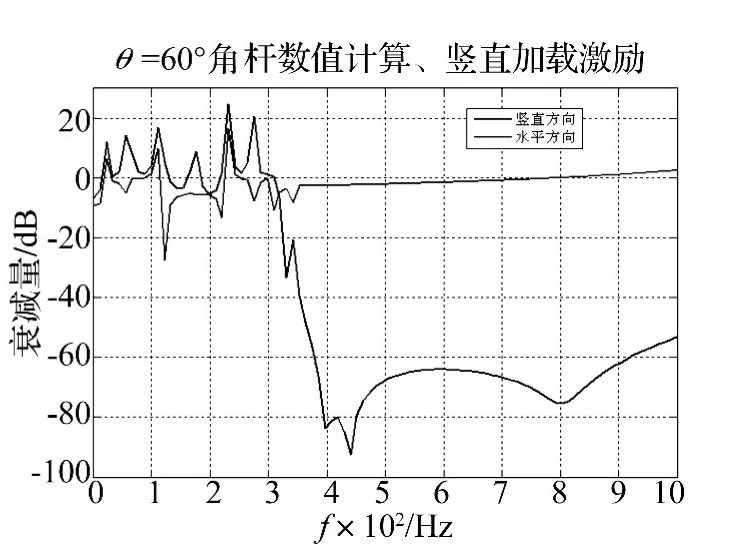
圖8 加載豎直位移激勵時60°角梁的傳遞率Fig.8 Transmissibility of 60-angle type beam being loaded vertical displacement excitation

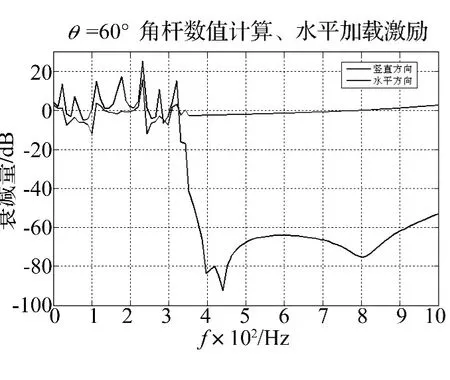
圖9 加載水平位移激勵時60°角梁的傳遞率Fig.9 Transmissibility of 60 － angle type beam being loaded horizontal displacement excitation

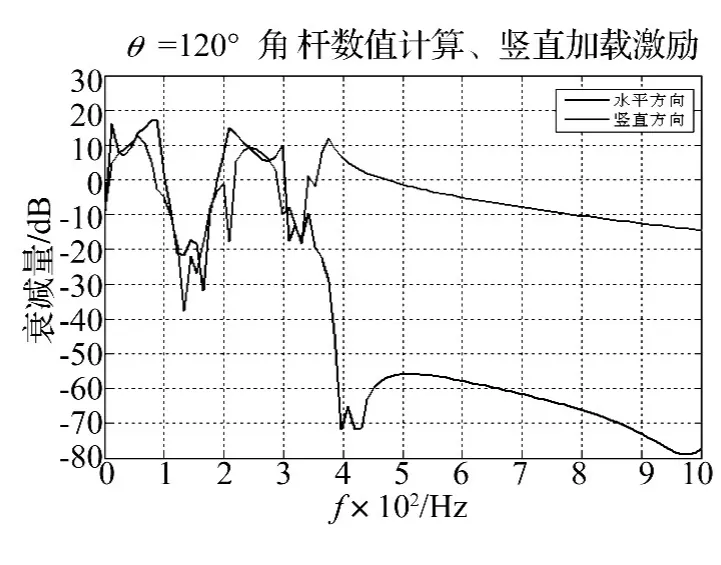
圖10 加載水平豎直位移激勵時120°角梁的傳遞率Fig.10 Transmissibility of 120-angle type beam being loaded vertical displacement excitation

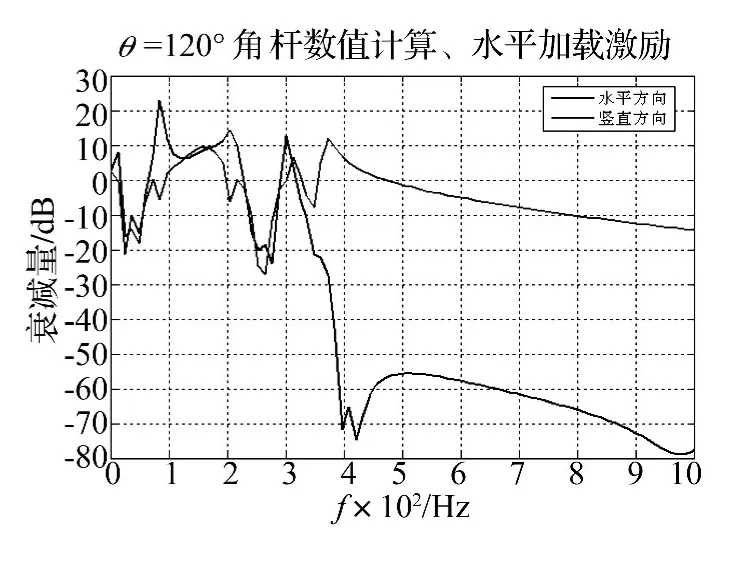
圖11 加載水平位移激勵時120°角梁的傳遞率Fig.11 Transmissibility of 120-angle type beam being loaded horizontal displacement excitation

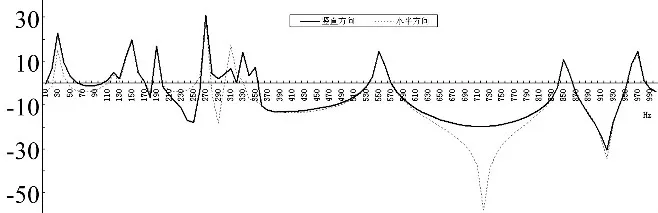
圖12 加載豎直位移激勵時角梁的傳遞率Fig.12 Transmissibility of angle type beam being loaded vertical displacement excitation

3 角式聲子晶體梁的有限元振動分析

首先考察豎直方向加載情況，在梁1下端給定豎直方向的諧位移激勵，分別測量梁2上端豎直方向和水平方向(紙面內(nèi))的位移，傳遞率計算結(jié)果如圖12所示。

該傳遞率曲線與數(shù)值計算結(jié)果(圖6)是基本吻合的，除了由于結(jié)構(gòu)的改變引入了兩個額外的共振峰(550 Hz和850 Hz)之外，在對應(yīng)梁的整個橫向帶隙內(nèi)，無論是在豎直方向還是在水平方向，均具有較好的減振效果，其范圍是:360～530 Hz，570～840 Hz，870～950 Hz，衰減量在－10～－20 dB之間。此外由于梁1與梁2形成了“彈簧－質(zhì)量”減振系統(tǒng)，因此在帶隙范圍之外的低頻區(qū)間幾個窄頻帶內(nèi)如210～260 Hz豎直方向也能獲得一定程度上的減振能力，但可能導(dǎo)致水平方向振動較為突出。圖13和圖14分別給出了橫向帶隙起止頻率處的角梁振動情況。在帶隙起始頻率處，基體梁基本不動，各局域振子振動方向反相;而在帶隙截止頻率處，各局域振子基本不動，基體整體作橫向振動。

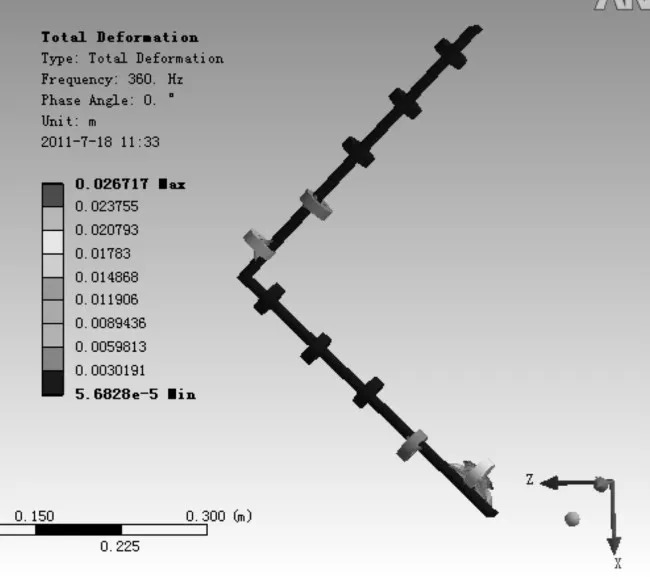
圖13 豎直方向加載時360 Hz處的角梁振動情況處Fig.13 Vibration of angle type beam at 360 Hz being loaded vertically

其次在梁1下端沿著水平方向(紙面內(nèi))加載，分別測量梁2上端豎直方向和水平方向的位移，計算所得的傳遞率如圖15所示。

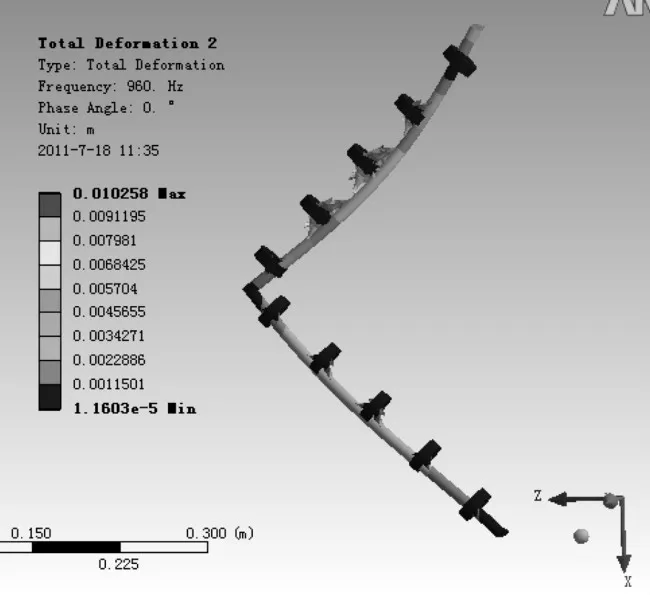
圖14 豎直方向加載時960 Hz的角梁振動情況Fig.14 Vibration of angle type beam at 960 Hz being loaded vertically

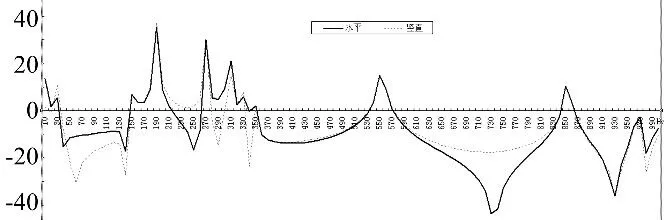
圖15 加載水平位移激勵時角梁的傳遞率Fig.15 Transmissibility of angle type beam being loaded horizontal displacement excitation

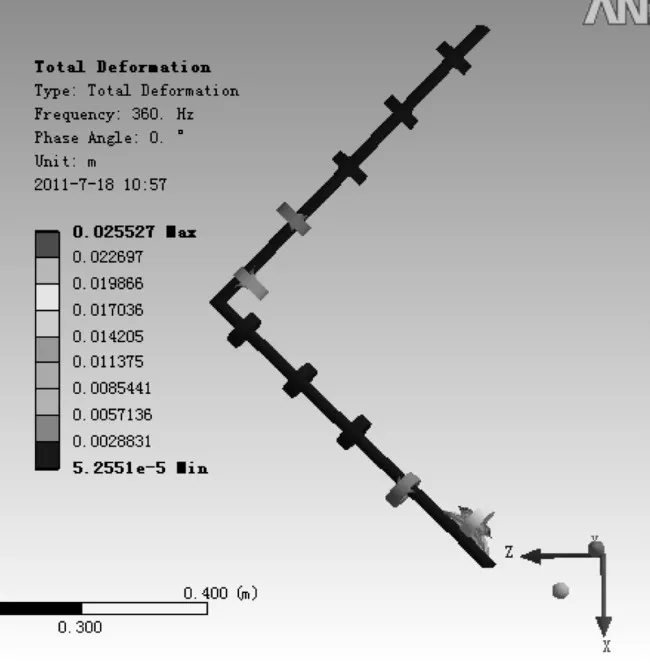
圖16 水平方向加載時360 Hz處的角梁振動情況Fig.16 Vibration of angle type beam at 360Hz being loaded horizontally

圖15表明，在對應(yīng)梁橫向帶隙范圍內(nèi)，除了550 Hz和850 Hz兩處結(jié)構(gòu)共振峰影響到了衰減外，無論是水平方向還是豎直方向，總體上也獲得了較好的減振性能。類似地，通帶范圍內(nèi)的低頻區(qū)(40～140 Hz;220～260 Hz)的減振性能也來自于兩梁構(gòu)成的“彈簧－振子”振系，其中40～140Hz范圍內(nèi)的減振效果在兩個方向上均能得到保證，并且衰減較大。該結(jié)果與數(shù)值分析結(jié)果(圖7)也是一致的。圖16和圖17給出了起止頻率處的振動情況，局域振子和基體的行為與豎直加載時的情況也是類似的，這也進(jìn)一步表明了角梁受到豎直和水平方向(面內(nèi))上的激擾時確實能夠通過波型的轉(zhuǎn)化從而使得兩梁的橫向帶隙得到較為充分的利用。

圖17 水平方向加載時960 Hz處的角梁振動情況Fig.17 Vibration of angle type beam at 960 Hz being loaded horizontally

4 結(jié)論

針對局域共振型聲子晶體梁和一類角式聲子晶體梁的振動進(jìn)行了傳遞矩陣法的數(shù)值計算，并采用有限元方法計算了3個平動方向的振動傳遞率，對比分析結(jié)果表明:

(1)所設(shè)計的局域共振型聲子晶體梁在0～1 000 Hz內(nèi)具有較寬較強的橫向振動帶隙和較窄較弱的縱向振動帶隙，分別位于170～180 Hz和360～900 Hz。聲子晶體梁可以很好地抑制梁軸線法平面內(nèi)的2維橫向振動，但同一頻帶內(nèi)軸線方向的縱向振動卻很難獲得有效的衰減，因而只具有二維減振能力;

(2)針對所設(shè)計的角式聲子晶體梁，90°夾角型式綜合減振效果強于60°和120°型式，在豎直方向和水平方向加載時，在除去兩處結(jié)構(gòu)共振峰(550 Hz和850 Hz)之外的橫向振動帶隙范圍內(nèi)(即360～530 Hz，570～840 Hz，870～950 Hz)均具有較強的振動衰減;在法線方向加載時，由于局域振子周期數(shù)的增加，在全帶隙內(nèi)均具有十分顯著的衰減;

(3)角式聲子晶體梁能夠通過波型轉(zhuǎn)化作用將縱向振動轉(zhuǎn)化為同頻率的橫向振動，從而有效地利用了橫向帶隙的強衰減作用和寬頻帶特性，實現(xiàn)了三維減振。

［1］溫熙森，溫激鴻，郁殿龍，等.聲子晶體［M］.北京:國防工業(yè)出版社，2009.

［2］Parobas I E，Sigalas M M.Elastic band gaps in a fcc lattice of mercury spheres in aluminum［J］.Phys.Rev.B，2002，66(5):052302.

［3］Liu Z，Chan C T，Sheng P.Analytic model of phononic crystals with local resonances［J］.Phy.Rev.B，2005，71(1):014103.

［4］Goffaux C，Sanchez-Dehesa J.Two-dimensional phononic crystals studied using a variational method:Application to lattices of locally resonant materials［J］.Phys.Rev.B，2003，67(14):144301.

［5］王 剛.聲子晶體局域共振帶隙機理及減振特性研究［D］.長沙:國防科技大學(xué)，2006.

［6］Wang G，Wen X S，Wen J H，et al.Quasi one-dimensional periodic structure with locally resonant band gap［J］.ASME Journal of Applied Mechanics，2006，73(1):167 －169.

［7］宋卓斐，王自東，王艷林，等.一維桿狀聲子晶體的帶隙特性［J］.振動與沖擊，2010，29(2):145 －148.SONG Zhuo-fei，WANG Zi-dong，WANG Yan-lin，et al.The characteristic of stop-band of a kind phononic crystal rod［J］.Journal of Vibration and Shock，2010，29(2):145－148.

［8］王 剛，溫激鴻，溫熙森，等.細(xì)直梁彎曲振動中的局域共振帶隙［J］.機械工程學(xué)報，2005，41(10):107 －110.WANG Gang，WEN Ji-hong，WEN Xi-sen，et al.Locally resonant elastic wave band gaps in flexural vibrations of slender beams［J］.Journal of Mechanical Engineering，2005，41(10):107 －110.

［9］劉耀宗，孟 浩，李 黎，等。基于遺傳算法的聲子晶體梁振動傳輸特性優(yōu)化設(shè)計［J］.振動與沖擊，2008，27(9):47－50.LIU Yao-zong，MENG Hao，LI Li，et al.Optimal design of vibrational transimission of sonic crystal beam based on genetical algorithm［J］.Journal of Vibration and Shock，2008，27(9):47 －50.

［10］Asiri S，Baz A，Pines D.Active periodic struts for a gearbox support system ［J］. SmartMaterialsAnd Structures，2006(15):1707－1714.