基于未加權區域采樣的直線反走樣算法

毛 峽 劉運龍 薛雨麗

（北京航空航天大學 電子信息工程學院，北京 100191）

光柵圖形顯示器由一系列離散像素組成，利用未加入反走樣技術的簡單直線生成算法（例如Bresenham算法［1］）繪制的非垂直非水平直線會在該類顯示器上出現明顯鋸齒狀或階梯狀邊緣［2］，在某種場合將會嚴重影響顯示效果.這種用離散量表示連續量引起的失真，稱為走樣（aliasing）；而用于減少或消除走樣的技術，稱為反走樣（anti-aliasing）［3］.反走樣在光柵圖形顯示［4－12］、共聚焦三維數據表面重建［13］、地圖可視化表達［14－15］等領域均有廣泛應用.

目前，直線反走樣技術主要有兩類：區域采樣和Wu算法.區域采樣又可分為未加權區域采樣和加權區域采樣，前者在確定顯示屏上某一像素灰度值時需要在重疊區域（該像素與代表直線的矩形相互重疊的部分）上對加權函數w（x，y）求積分，此加權函數恒為1；后者計算方法與前者相同，只是所選加權函數w（x，y）不恒為1.Wu算法［7－8］基于距離加權確定像素灰度值，其在二像素寬直線的反走樣方面至今仍是經典解決方案［2］.

對于具有多灰度的光柵圖形顯示器，未加權區域采樣和加權區域采樣通過控制像素灰度緩慢變化從而很好地實現反走樣.至今，以加權和未加權區域采樣算法為基礎已延伸出多種能有效解決直線走樣問題的算法［5－9］.

文獻［5］從頻域的角度剖析走樣現象產生的機理，并將二維圓錐形濾波器應用于直線反走樣，雖然該加權區域采樣算法能取得很好的反走樣效果，但是由于該算法在計算像素與理想直線的距離時需要用到浮點數加法和乘法，并且在確定灰度值時用到了取整運算，這些運算利用FPGA（Field Programmable Gate Array）實現所需周期過多，不利于FPGA硬件的快速實現.

文獻［6］給出一種基于加權區域采樣的離散化算法，在確定像素灰度值時不再使用運算量很大的積分運算，算法效率相對于傳統算法更優，但是該算法在計算當前像素灰度值時仍會用到浮點運算以及類型強制轉換運算，不利于FPGA硬件實現.

文獻［7］和文獻［8］提出了經典Wu直線反走樣算法.相比于Bresenham算法，利用 Wu直線反走樣算法生成的直線能達到很好的平滑效果，但是Wu算法需要用到較多的浮點數乘法和取整運算，計算比較復雜.

文獻［9］分析了屏幕正方形像素和一個像素寬直線條相交的7種情況，并給出相應的重疊區域面積計算方法，該方法用到了不利于FPGA硬件實現的除法運算.

綜上所述，為實現反走樣，傳統區域采樣和Wu算法使用大量不利于FPGA硬件實現的運算.本文通過結合Bresenham算法和傳統未加權區域采樣的思想，提出一種利于FPGA硬件實現的反走樣直線生成新算法.

1 直線生成與反走樣概述

1.1 直線生成算法

計算機圖形學中的直線生成算法（或直線掃描轉換算法）通過在光柵圖形顯示器上尋找與理想直線距離最近的一系列離散像素近似表示直線.

目前生成單像素寬直線的算法主要有3種：數值微分法、中點畫線法和Bresenham算法［16］.

1.1.1 數值微分法

數值微分法是最簡單、直觀的直線生成算法.假設擬生成直線的斜率處于0～1之間（其它情況可通過先轉換x和y軸再處理），算法原理為：沿著x軸方向根據直線斜率從起點到終點依次確定與直線距離最近的一組離散像素.

由于該算法中的像素縱坐標y和直線斜率k必須用浮點數表示，且每次循環計算均需對y進行舍入取整，所以該算法不利于FPGA硬件實現.

1.1.2 中點畫線法

假設擬生成直線的斜率處于0～1之間，若直線在x方向增1，則在y方向的增量只能在0～1之間.中點畫線法的思想為：將當前列（設橫坐標為x0）與直線距離最近的兩個像素（x0，y0），（x0，y0＋1）的中點坐標（x0，y0＋0.5）代入函數F（x，y）（F（x，y）＝0為直線方程）；若F（x0，y0＋0.5）≥0，認為當前列屬于直線的點為（x0，y0）；若F（x0，y0＋0.5）＜0，則認為當前列屬于直線的點為（x0，y0＋1）.

經過簡單換算后，中點畫線法只包含整數加減及比較運算，因此該算法利于FPGA硬件實現.

1.1.3 Bresenham算法

Bresenham 算法［1，17－18］被公認為最有效的直線生成算法.假設擬生成直線的斜率處于0～1之間，該算法基本思想是：直線每走一步，橫坐標x改變一個像素單位，縱坐標y根據誤差項e的符號決定是否改變.

Bresenham算法同樣可改寫為只包含整數加減及比較運算的形式，因此該算法利于FPGA硬件實現.

1.2 區域采樣直線反走樣算法

區域采樣直線反走樣算法的提出基于兩點假設：第一，將像素看成有一定面積的規則區域（本文將像素看成互不相交的正方形）；第二，擬生成直線段并非無寬度理想線段，而是一個寬度至少為一個像素單位的線條.如圖1所示，正方形代表一個像素，內部實心圓點為像素中心，矩形代表擬生成的單像素寬線條，虛線為矩形中軸線.

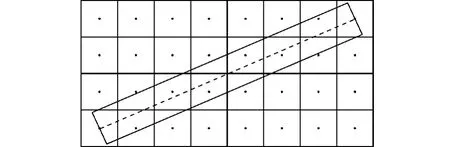
圖1 代表直線的矩形和代表像素的正方形

區域采樣算法可分為未加權區域采樣與加權區域采樣兩類.由于加權區域采樣所用到的加權函數w（x，y）不恒為1，因此需要花費大量計算用于確定在重疊區域上對w（x，y）所求的積分，而未加權區域采樣則只需計算重疊區域的面積，因此，未加權區域采樣的運算量往往少于加權區域采樣.然而，未加權區域采樣在計算重疊面積時仍需大量浮點數乘法，在確定像素灰度值時需用到舍入運算，這些運算使該算法復雜度過高，不利于FPGA硬件實現.

1.3 Wu直線反走樣算法

Wu直線反走樣算法［7－8］是計算機圖形學反走樣技術領域較早使用的一種經典算法，適用于生成二像素寬的反走樣直線.Wu算法實際上是一種基于距離加權的反走樣算法，其基本思想為：沿長軸方向前進一個像素單位，在短軸方向有兩個像素距離理想直線最近，灰度值由它們與直線的距離確定，距離越近灰度值越大，兩個像素灰度值之和等于像素顏色的最大灰度.

由于Wu直線反走樣算法能滿足通常需求且算法本身計算不復雜，因此該算法在很多場合得到廣泛應用.

2 新的直線反走樣算法

鑒于傳統未加權區域采樣直線反走樣算法不利于FPGA硬件實現，本文將Bresenham算法與未加權區域采樣思想相結合，提出一種利于FPGA硬件實現的直線反走樣算法，該算法可用于快速生成三像素寬的反走樣直線段.

2.1 算法的基本原理

本文算法的應用前提是光柵圖形顯示器支持多級灰度顯示，例如64級和256級.

算法的基本原理是將與矩形區域有重疊的像素均分為M個子像元，M等于灰度級數，通過統計被覆蓋子像元的數量確定像素灰度值.例如，若某像素被覆蓋子像元數量為N，則該像素灰度值為N－1，特殊地，若N＝0，則像素灰度值為0.

2.2 算法的實現

2.2.1 非端點部分的處理

圖1的實線矩形框代表擬生成的直線段，虛線為矩形的中軸線，介紹本文算法的具體實現時只討論直線斜率處于0～1之間的情況，其余斜率情況可通過將x和y軸互換處理.本文算法流程如圖2所示.

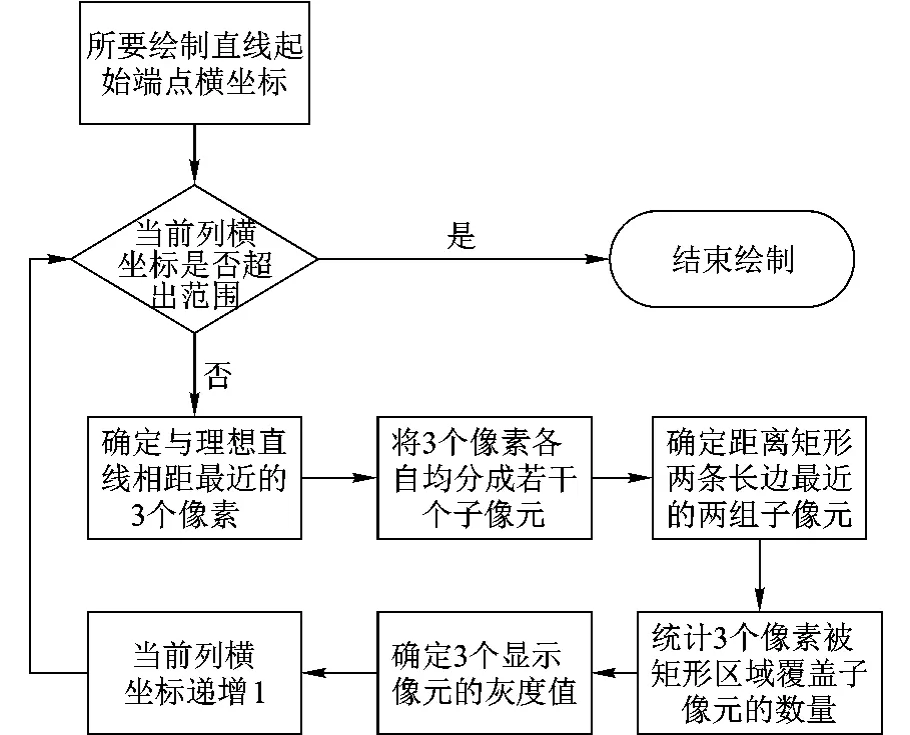
圖2 本文算法流程圖

假設光柵圖形顯示器支持256級多灰度顯示，結合圖1與圖2將本文算法主要步驟敘述如下：

1）判斷當前列是否被矩形區域覆蓋.

由于擬生成直線的起點坐標（x0，y0）和終點坐標（x1，y1）已知，因此只需判斷當前列的橫坐標X是否處于x0～x1的范圍內即可.若X處于x0～x1之間，說明當前列存在被矩形區域覆蓋的現象，執行步驟2）操作；否則，直接結束該直線的生成操作.

2）確定當前列可能有灰度值的3個像素.

由圖1可知，單像素寬的直線段在當前列最多與3個相鄰像素存在重疊區域，其中處于中間位置的像素距離虛線最近，而該像素坐標可通過對虛線應用Bresenham算法快速地進行確定.假設中間像素的坐標為（Xmid，Ymid），則另外兩個像素的坐標分別為（Xmid，Ymid＋1）和（Xmid，Ymid－1）.

3）均勻分割步驟2）中確定的3個像素.

根據算法原理，將3個像素各自均勻分割成數量等同于灰度級數的子像元.由于假設光柵顯示器的灰度級數為256，因此可將像素均勻分割為16×16子像元，圖3給出像素的分割示意圖.

圖3 像素均勻分割結果示意圖

4）確定當前列距離矩形兩邊最近的兩組子像元.

根據Bresenham算法可快速確定這兩組子像元，其中每組包含16個子像元.這兩組子像元給出矩形區域在當前列覆蓋的邊界情況.圖4給出當前列矩形兩邊經過Bresenham算法確定的兩組子像元.

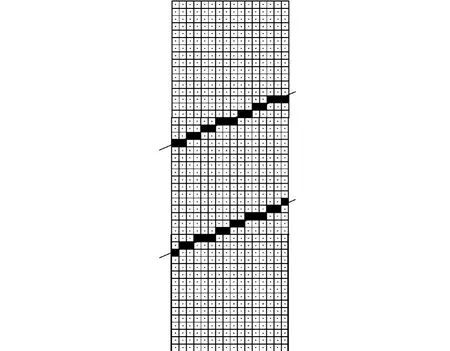
圖4 當前列確定的兩組子像元

5）統計3個像素被矩形區域覆蓋的子像元數量.

根據步驟4）確定的兩組子像元，依次統計當前列（共包含16個子列）每一個子列分別屬于3個像素的子像元數量，最后將16個子列的統計結果進行累加，從而得到3個像素被矩形區域覆蓋的子像元數量.

6）確定像素灰度值.

3個像素的灰度值分別等于各自被矩形區域覆蓋的子像元數量減1，例如，假設像素（x，y）共有N個子像元被矩形區域覆蓋，則該像素的灰度值應為N－1，特殊地，若N＝0，則灰度值為0.接著，將記錄當前列的橫坐標X增1，繼續執行步驟1）操作.

2.2.2 端點部分的處理

在確定直線端點（起點和終點）所在列像素灰度值時不能直接采用上述方法，而需進一步分析.

圖5給出直線起始端點的放大圖，在直線斜率不為0時，矩形兩邊的起點（P1和P5）橫坐標不相等（斜率為0時，兩橫坐標相等）.這時，利用Bresenham算法確定兩組子像元并統計圖中像素被覆蓋子像元的數量將會存在一定困難.

考慮到圖中三角形A區域（由P1，P2和P3確定）與三角形B區域（由P3，P4和P5確定）面積相等，因此有

式中，NA與NB分別表示區域A與B覆蓋的子像元數量.

此外，還有

式中，C為由P2，P3，P5，P8，P7和P6確定的多邊形區域.

根據式（2）可知，確定圖中像素的灰度值只需統計B＋C區域的子像元數量，由于B＋C區域兩條邊界的起點（P2和P4）橫坐標相同，此時以P2，P4為起點利用Bresenham算法確定圖5中的像元所在列的兩組子像元后，即可方便地統計出該列各個像元中被矩形區域覆蓋子像元的數量，從而確定該列像元的灰度值，可見以P2，P4作為矩形兩長邊的等效起點可簡化統計被覆蓋子像元的步驟.利用類似方法可簡化直線段終點所在列像素灰度值確定的工作，這里不再詳細說明.

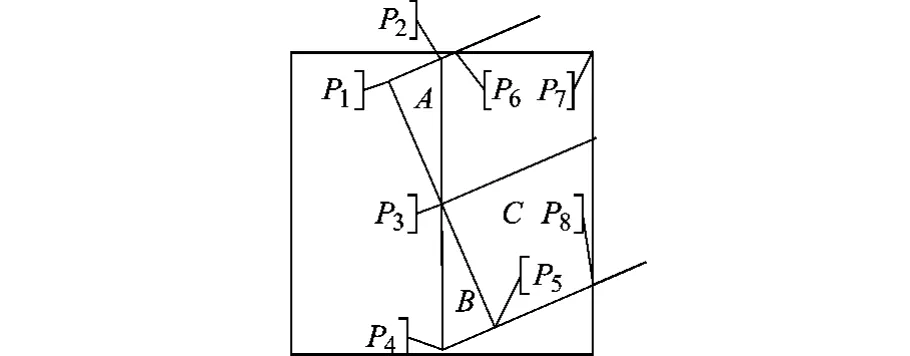
圖5 直線起始端點放大示意圖

3 實驗結果與分析

本文分別從仿真速度與運算次數統計、反走樣效果兩個方面將傳統未加權區域采樣算法、Wu算法以及本文算法進行對比.

3.1 仿真速度與運算次數統計

為驗證本文算法仿真速度，在Pentium（R）2.80GHz雙核、內存3GB的計算機，用 MATLAB 7.11.0編程完成傳統未加權區域反走樣算法、Wu算法以及本文提出的反走樣算法，利用這3種算法分別計算3條擬生成直線所有像素的坐標和灰度值.表1給出3條直線的起點和終點坐標，表2給出3種算法分別生成3條直線所需時間.

表1 3條直線的起點和終點坐標

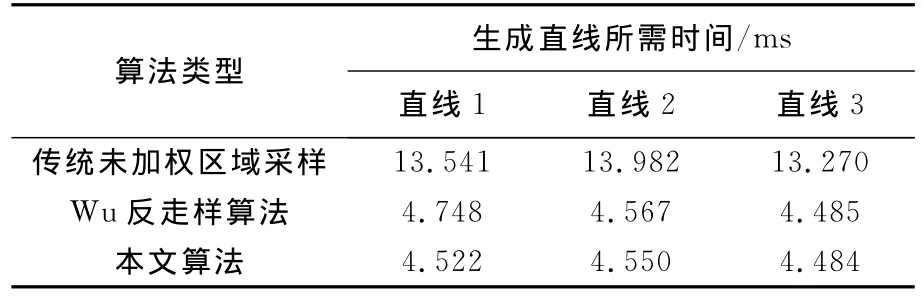
表2 3種算法生成3條直線所需時間對比

由表2可知，本文算法在軟件平臺上生成直線的效率約比傳統未加權區域采樣算法快2倍，與經典Wu算法效率相差不大.但是Wu算法在確定像素灰度值時需用到大量浮點數乘法、四舍五入以及浮點數加減法，這些運算對于FPGA硬件來說較復雜，執行效率不高.本文算法將傳統未加權區域采樣算法中的浮點運算轉換為整數加減法運算，確保算法易于FPGA硬件實現.表3為3種算法分別生成直線1所需執行的各種運算次數統計表.

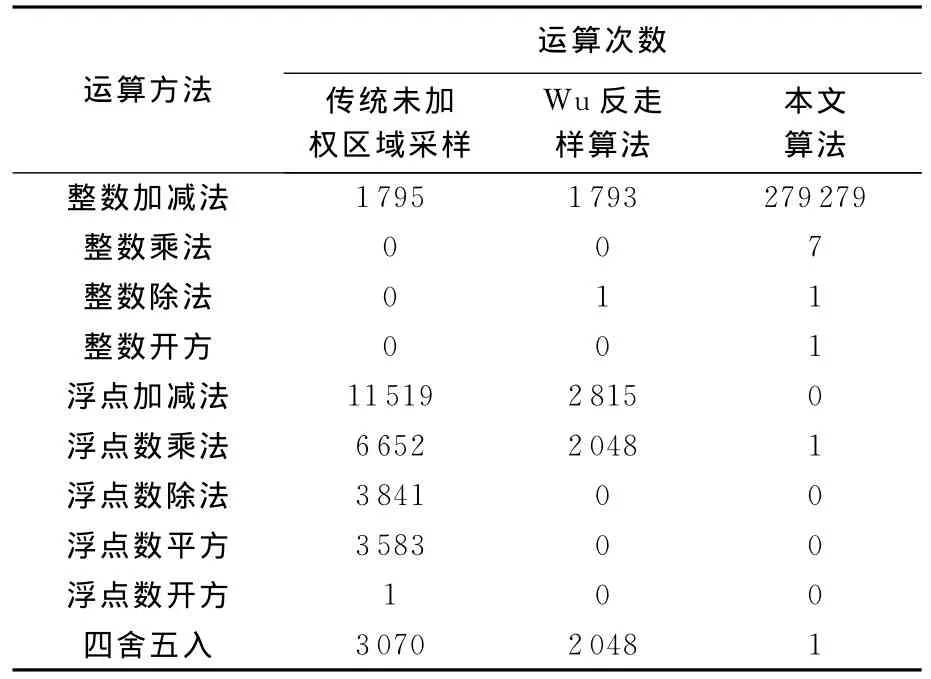
表3 3種算法生成直線1所需運算次數統計

可見，本文算法主要運算由整數加減法完成，利于FPGA硬件實現，能達到FPGA硬件加速目的.

3.2 反走樣效果

為驗證本文算法的反走樣效果，利用MATLAB 7.11.0軟件仿真平臺完成基于Bresenham算法以及3種反走樣算法生成直線1與直線2的任務.圖6的4個子圖分別是對應算法仿真結果放大8倍后的效果圖，圖7的兩個子圖分別給出Wu算法與本文算法仿真結果放大16倍后的效果圖.

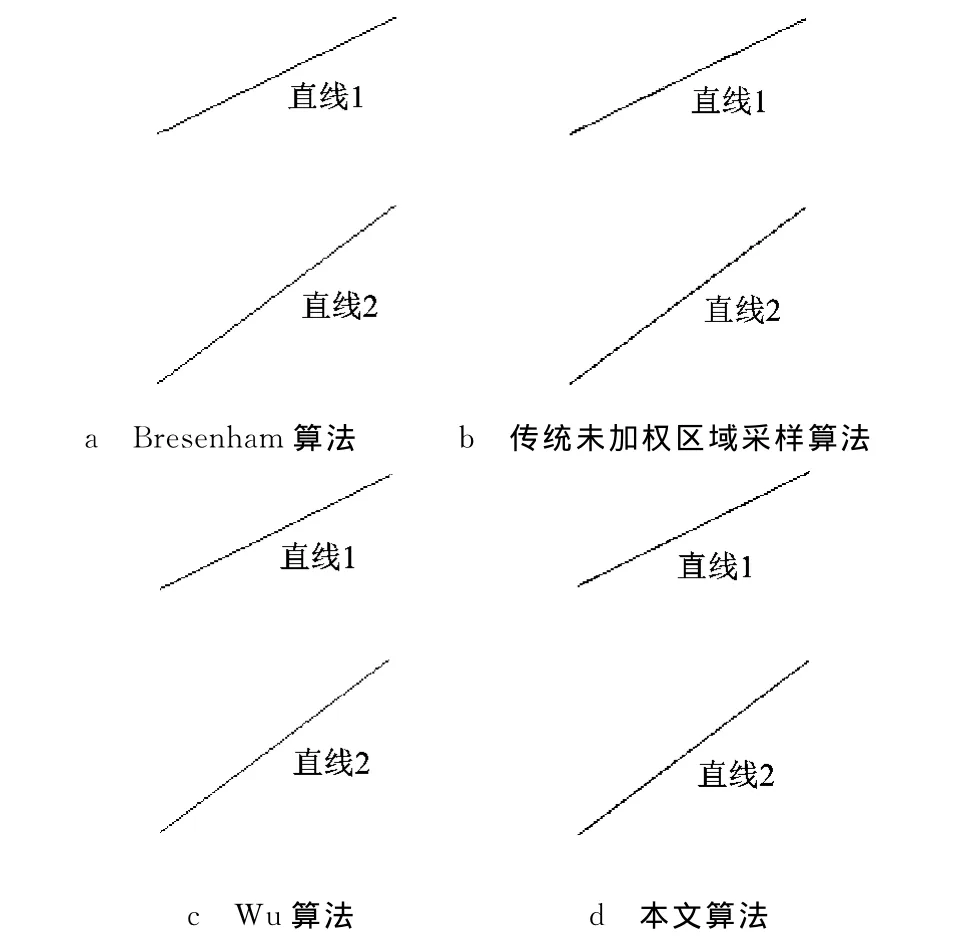
圖6 4種算法仿真結果圖

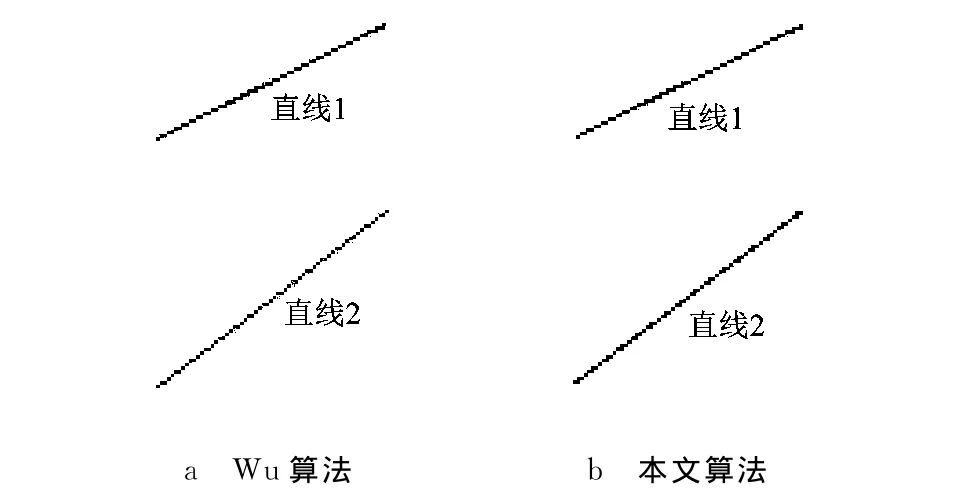
圖7 Wu算法與本文算法仿真效果圖對比

對比并分析圖6與圖7的各個子圖，可得如下4個分析結果：

1）由于Bresenham算法沒有加入反走樣思想，因此由該算法所得直線（圖6a）邊緣存在明顯鋸齒狀或階梯狀，而由另外3種反走樣算法生成所得直線（圖6b、圖6c和圖6d）明顯比圖6a的平滑；

2）Wu算法生成的反走樣直線（圖6c）平滑效果較好，但是直線整體灰度偏低，這是由于Wu算法用于生成二像素寬直線，在短軸方向距離直線最近的兩個像素點灰度之和僅為像素顏色的最大灰度，從而造成直線整體灰度降低；

3）對比圖6的后3個子圖可知，由本文算法（圖6d）與傳統非加權區域采樣算法（圖6b）分別生成的直線平滑度相差不大，這兩種算法生成的直線整體灰度比Wu算法直線高，使得直線看起來更清晰；

4）對比圖7的兩個子圖可知，由于Wu算法基于距離加權計算像素灰度值，所以沿著直線方向，Wu算法所得直線某些相鄰像素灰度值相差較大，遠處觀看時由該算法生成的直線會出現“斷斷續續”的現象，而基于面積加權的本文算法相鄰像素灰度值差異則較小.

綜上所述，相比于Wu算法，本文算法的反走樣效果更佳.

4 結 束 語

通過結合Bresenham算法以及未加權區域采樣的思想，本文提出一種符合FPGA硬件實現特點的反走樣直線生成新算法.本文算法可用于在支持多灰度的光柵圖形顯示器上生成三像素寬的反走樣直線.本文算法摒棄傳統算法使用大量不利于FPGA硬件實現的浮點運算，而主要采用整數加減法實現，因此易于FPGA硬件實現.仿真結果表明：本文算法不但反走樣效果比Wu算法更好，而且仿真效率遠高于傳統未加權區域采樣算法.

（References）

［1］Bresenham J E.Algorithms for computer control of a digital plotter［J］.IBM Systems Journal，1965，4（1）：25－30

［2］李震霄，何援軍.任意寬度直線的繪制與反走樣［J］.武漢大學學報，2006，39（4）：130－133

Li Zhenxiao，He Yuanjun.Arbitrary width line generation and anti-aliasing［J］.Journal of Wuhan University，2006，39（4）：130－133（in Chinese）

［3］孫家廣，楊長貴.計算機圖形學［M］.北京：清華大學出版社，1998 Sun Jiaguang，Yang Changgui.Computer graphics［M］.Beijing：Tsinghua University Press，1998（in Chinese）

［4］牛連強，張丹，陶峰.直線的光柵轉換算法與快速反走樣繪制技術［J］.沈陽工業大學學報，2012，34（1）：73－78

Niu Lianqiang，Zhang Dan，Tao Feng.Raster-conversion algorithm and fast anti-aliased drawing technique for line［J］.Journal of Shenyang University of Technology，2012，34（1）：73－78（in Chinese）

［5］沈強，張波，陳淑珍，等.計算機圖形學反走樣技術及實現［J］.武漢大學學報，1997，43（1）：113－118

Shen Qiang，Zhang Bo，Chen Shuzhen，et al.Antialiasing technique and applications in computer graphics［J］.Journal of Wuhan University，1997，43（1）：113－118（in Chinese）

［6］杭后俊，付 勇.一種基于加權區域采樣的直線反走樣生成算法［J］.計算機技術與發展，2009，19（6）：138－141

Hang Houjun，Fu Yong.One antialiasing algorithm based on weighting region sampling［J］.Computer Technology and Development，2009，19（6）：138－141（in Chinese）

［7］Wu Xiaolin，Rokne J G.Double-step incremental generation of lines and circles［J］.Computer Vision，Graphics and Image Processing，1987，37（3）：331－344

［8］Wu X.An efficient anti-aliasing technique ［J］.Computer Graphics，1991，25（4）：143－152

［9］孔令德.基于面積加權反走樣算法的研究［J］.工程圖學學報，2009，4：49－54

Kong Lingde.Research on area-weighted antialiasing algorithm［J］.Journal of Engineering Graphics，2009，4：49－54（in Chinese）

［10］婁劍濤，王秀和.基于對稱的反走樣直線生成算法［J］.計算機工程與應用，2011，47（1）：173－175

Lou Jiantao，Wang Xiuhe.Anti-aliasing line drawing algorithm based on symmetry［J］.Computer Engineering and Applications，2011，47（1）：173－175（in Chinese）

［11］袁一鳴，段鳳陽，李贊平.羅盤儀表繪制中快速反走樣算法的研究［J］.艦船電子工程，2011，31（9）：60－62

Yuan Yiming，Duan Fengyang，Li Zanping.Research on fast anti-aliasing algorithm in compass display［J］.Ship Electronic Engineering，2011，31（9）：60－62（in Chinese）

［12］張鵬，王良.嵌入式圖像系統的改進Bresenham反走樣算法的應用［J］.電子設計工程，2011，19（4）：117－119 Zhang Peng，Wang Liang.Application of improved Bresenham anti-aliasing algorithm based on embedded image system［J］.Electronic Design Engineering，2011，19（4）：117－119（in Chinese）

［13］薛斌黨，姜志國，周孝寬.共聚焦三維數據表面重建的一種反走樣方法［J］.北京航空航天大學學報，2005，31（10）：1054－1057

Xue Bindang，Jiang Zhiguo，Zhou Xiaokuan.Anti-aliasing technique for surface reconstruction of confocal data［J］.Journal of Beijing University of Aeronautics and Astronautics，2005，31（10）：1054－1057（in Chinese）

［14］梅洋，李霖，賀彪.基于邊界反走樣算法的地圖可視化研究［J］.武漢大學學報，2008，33（7）：759－761

Mei Yang，Li Lin，He Biao.Cartographic visualization based on boundary anti-aliasing［J］.Journal of Wuhan University，2008，33（7）：759－761（in Chinese）

［15］鄧術軍，郭建星.一種適合于地圖出版符號的反走樣算法研究［J］.武漢大學學報，2005，30（12）：1120－1123

Deng Shujun，Guo Jianxing.An anti-aliasing algorithm suitable to map publishing symbol［J］.Journal of Wuhan University，2005，30（12）：1120－1123（in Chinese）

［16］Foley J D.計算機圖形學導論［M］.北京：機械工業出版社，2004

Foley J D.Introduction to computer graphics［M］.Beijing：China Machine Press，2004（in Chinese）

［17］Li Xiang，Shao Xiaoyan.Fast line drawing algorithm by circular subtraction based on Bresenham［J］.Proceeding of SPIE，2012，83490L：1－6

［18］Norbert Spie，Michael Zapf，Nicole V Ruiter.Evaluation of the Bresenham algorithm for image reconstruction with ultrasound computer tomography［J］.Proceeding of SPIE，2011，796803：1－9