基于虛擬參考迭代整定方法的永磁同步電機優化重復控制
聶成翔, 陳志盛
(長沙理工大學可再生能源電力技術湖南省重點實驗室,湖南長沙410076)
永磁同步電機運行原理與普通電激磁同步電機相同,但它以永磁體代替了激磁繞組,提升了電機運行的可靠性[1-2]。20世紀60年代以后,永磁同步電機開始應用于交流變頻調速系統,到20世紀80年代后,由于新型電力電子器件的不斷涌現,極大地促進了永磁同步電機調速系統的發展。
FRIT即虛擬參考迭代整定[3],它是一種專門用來設計未知模型反饋控制器的,它能優化其性能指標,包括虛擬參考的一次性實驗輸出計算,使其系統性能得到相對穩定等。對于對象模型未知的系統,以及周期信號在測量不到的情況下,FRIT具有很大的運用空間。
重復控制是一種以內模原理為基礎的控制策略[4]。內模原理就是如果想讓控制系統對某一參考指令實現無靜差跟蹤,那么該參考指令的模型必須包含在穩定的閉環控制系統內部。如果伺服系統[5]要滿足對穩定性和動態性能的魯棒性,即當系統參數發生變化時仍能保持穩定性、穩態偏差為零和過渡響應不受參數變化的影響,那么設計的重復控制器就可以解決問題。
1 永磁同步電機調速系統數學模型
如圖1所示,基于矢量控制的永磁同步電機調速系統主要由電流檢測、轉速和位置檢測、坐標變換、空間矢量脈寬調制(SVPWM)、電流調節器、轉速調節器等環節組成[6]。系統中的電流環和轉速環通常采用PID型算法控制。
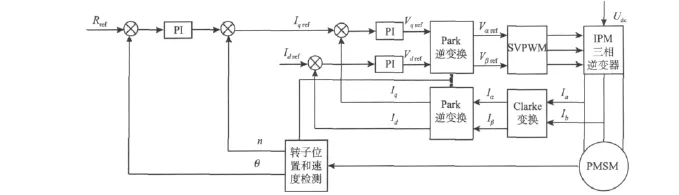
圖1 永磁同步電機矢量控制原理Fig.1 PMSM vector control principle diagram
當永磁同步電動機結合矢量控制法作為被控對象時,常用其d-q軸下的數學模型進行分析,其定子磁鏈方程為
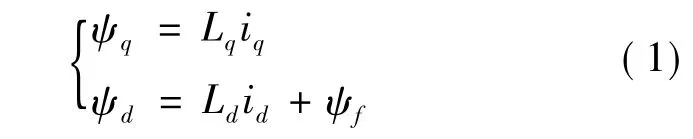
定子電壓方程為
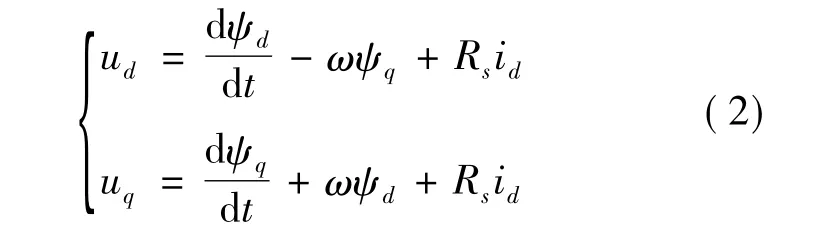
其中:Rs為電樞繞組電阻;Lq,Ld分別為d,q線圈的等效繞組電感;ψf為永磁體產生的等效磁鏈,其值為常數;id,iq為定子電流合成矢量在d,q軸上的分量;ω為轉子電角速度。
永磁同步電機的運動方程為
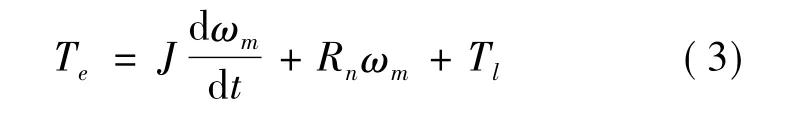
其中:Tl為負載轉矩,正方向與Te相反;Rn為運動阻尼系數;J為電機與負載轉動慣量之和;ωm為轉子機械角速度,其中機械角速度與電角速度的關系為ω =npωm;Te與ωm的正方向相同。
2 基于FRIT的重復控制器設計
2.1 重復控制器設計原理
重復控制是基于內模原理的一種控制方法。Francis和Wonham[7]提出的內模原理,在伺服系統控制中起著相當重要的作用。內模原理是指如果在一個穩定的閉環系統內設置一個可以產生與參考輸入信號相同的信號發生器,則系統輸出可以無穩態誤差的跟蹤輸入指令。Inoue[8]等人基于上述思想提出了重復補償控制理論[9-10],利用內模原理,在穩定閉環系統內設置一個可以產生與參考輸入同周期的內部模型,從而使系統實現對外部周期參考信號的漸近跟蹤。
圖2為簡單的單輸入、單輸出閉環系統。
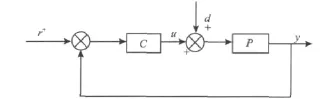
圖2 基本閉環系統Fig.2 Basic closed loop system
由圖2不難看出,這是一個單輸入、單輸出、連續時間且時間不變的閉環系統。注意到C(ρ)為PID控制器中的反饋控制器,其表達式:
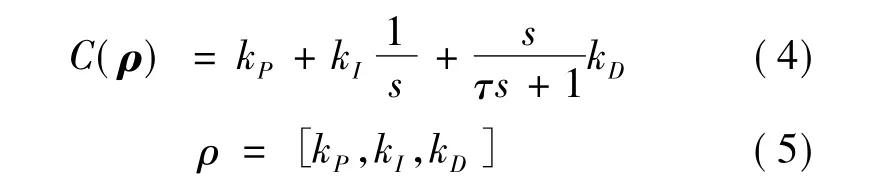
其中,kP,kI,kD分別為比例、積分、微分增益項,τ 是個很小的正實數,令u0,y0是此系統的輸入輸出,當參考信號τ應用于閉環系統時,C(ρ0)成立,其中ρ0是一個控制器的初始參數向量,假定控制器C(ρ0)閉環穩定,且ρ0保持不變。
為減小跟蹤誤差,有效地增大運行帶寬,提出改進型重復控制器,P為控制對象,C為PID控制器,r為輸入,y為輸出,d為外部擾動。此外,參考模型的擾動響應Pdr和參考模型的輸出擾動d中有關系式ydr=Pdrd。那么在模型不確定時系統的初始輸入輸出數據u0,y0由虛擬信號的輸入得到。但是此系統的跟蹤性仍然不很精確,加之存在外部輸入擾動信號時,系統不能得到很好的抑制。為了使此系統減小不確定干擾而造成的輸出畸變,使得穩態下輸出能很好地跟蹤參考信號,設計了一個插入式的重復補償控制器如圖3所示。
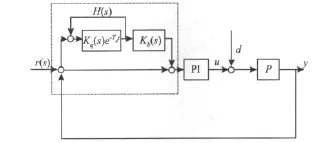
圖3 改進型重復控制系統Fig.3 Improved repeat control system
圖3中虛線部分的傳遞函數為
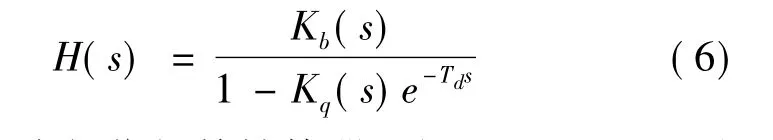
其中,Kb(s)為相位超前補償器。設 Kb(s)=eτbs,這里τb是非負常數。Kq(s)為一個低通濾波器,Td為滯后時間,其取值與期望輸入信號的周期相同。低通濾波器Kq(s)僅允許輸入信號特定的諧頻通過,受低通濾波器帶寬ωq的限制,重復控制系統的跟蹤誤差在穩態時不可能為零。
改進后的重復控制系統,由于插入了一個重復補償控制器,使得穩態輸出下能快速精確地跟蹤參考信號,系統的精確性和快速性得到了很大地提升。
2.2 FRIT整定PID擾動衰減
FRIT中引入了虛擬參考信號,從圖3中可得到
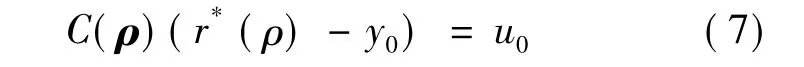
虛擬參考信號r*(ρ)轉化得到
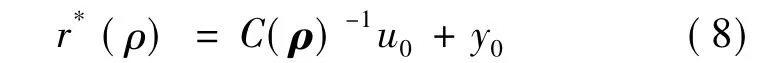
式中,y0設定為閉環系統的輸出,C(ρ0)在理想的擾動響應下且虛擬信號r*(ρ)是增強的,因此,由公式(8)得到
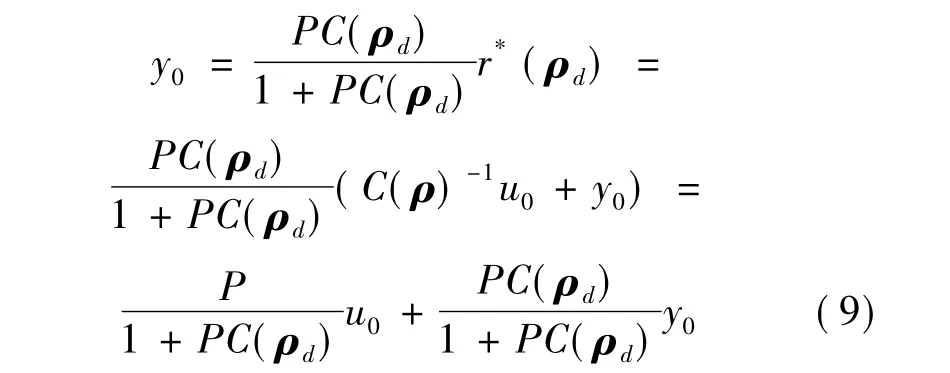
假設存在參數向量ρd做為理想控制參數向量,那么閉環傳遞函數中從擾動d到輸出y符合參考擾動響應模型,即等式假設成立。令Pr是參考模型的理想參考信號響應,ρd是存在Pr的閉環系統中理想控制器的參數向量,Pr即滿足
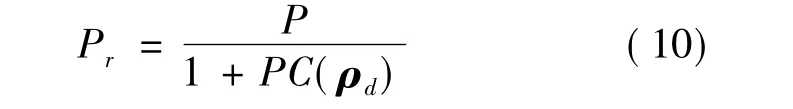
因此式(9)可以轉化為
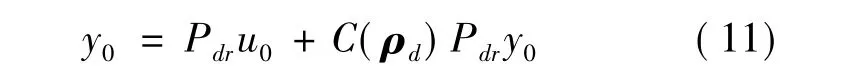
FRIT驗證理想控制器參數向量ρd是根據公式(11)與模型中的一次實驗輸入輸出數據u0,y0得到的。令

為了獲得最小的優化控制器參數向量,對ˉy(ρ)和y0采用積分平方誤差的方法求得
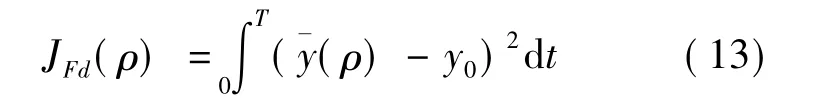
其中優化參數向量為
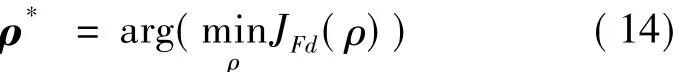
3 數值仿真與分析
通過以上對FRIT算法的推導,由公式(4),(12)可以得到FRIT優化算法的整體模型如圖4所示。
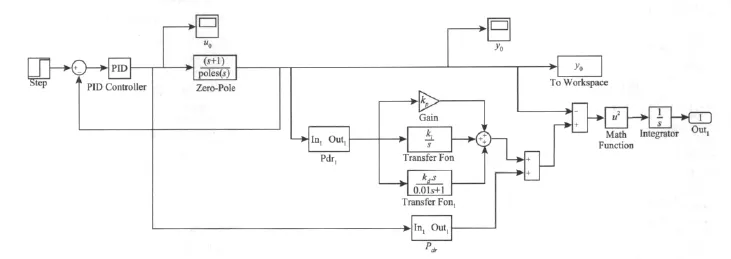
圖4 FRIT算法模型Fig.4 FRIT algorithm model
對于PID控制的FRIT優化參考模型,假定不確定對象模型P(s)可以表示為
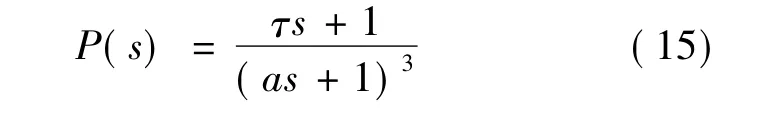
其中a=1,為一個很小的常數;y0和u0假定為在存在擾動信號r下閉環系統的初始輸出輸入數據,且初始PID參數定義為kP=0.5,kI=0.5,kD=0.2,初始PID增益的輸入輸出數據如圖5所示。
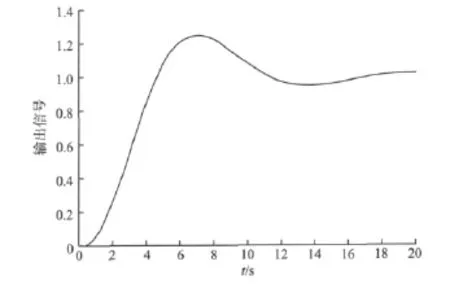
圖5 初始PID參數擾動響應Fig.5 Initial PID parameters disturbance response curve
假定參考模型Pdr(s)定義為
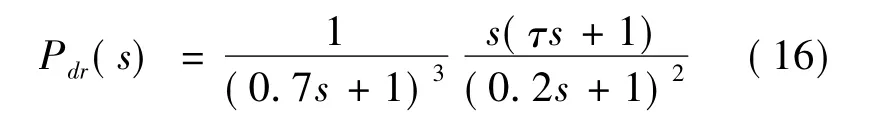
且PID控制器的參數設定為kP=2.427 1,kI=0.999 9,kD=1.507 1。圖6為PID參數調整后的擾動響應曲線圖。
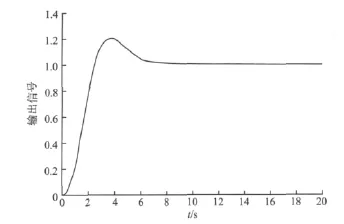
圖6 PID參數調整后擾動響應Fig.6 Initial PID parameters disturbance response curve
對于永磁同步電機模塊電機參數設置為:額定轉速ne=1 000 r/min,額定轉矩Te=2 N·m,額定功率Pe=8 000 W,額定電壓Ue=380 V,同步電感Ld=8.5×10-3H,定子相繞組電阻R=5.57 Ω,轉動慣量J=0.8×10-3kg·m2,轉子磁通ψf=0.243 Wb。
通過永磁同步電機的仿真模型能得到轉速、轉矩和相電流的相應曲線如圖7~9。
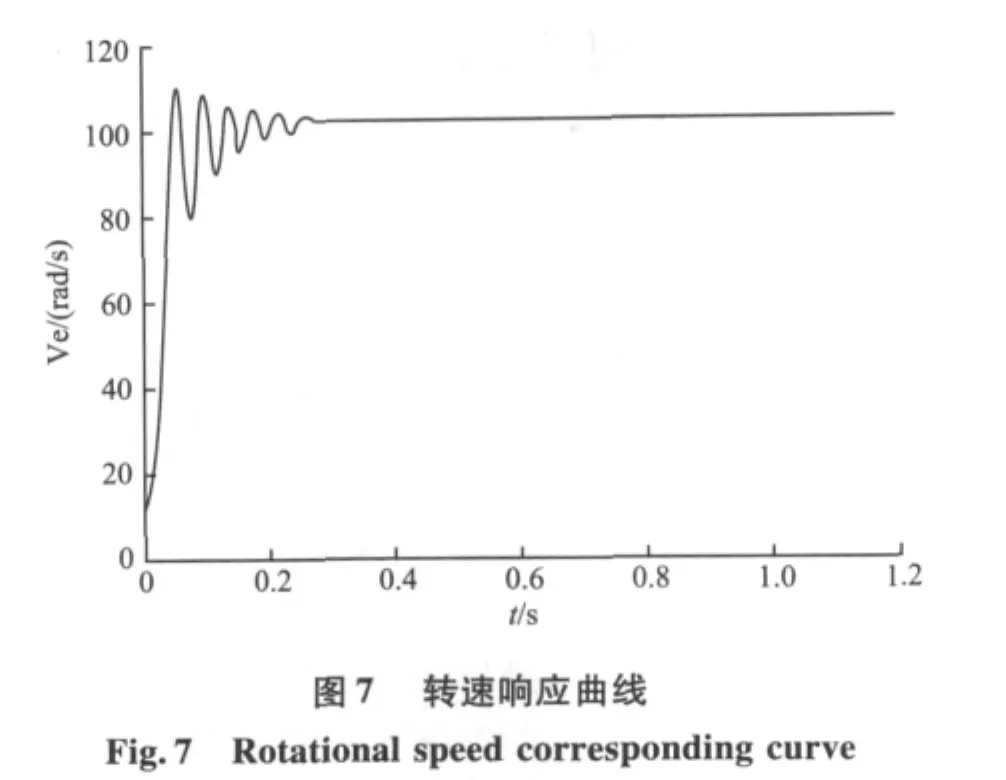
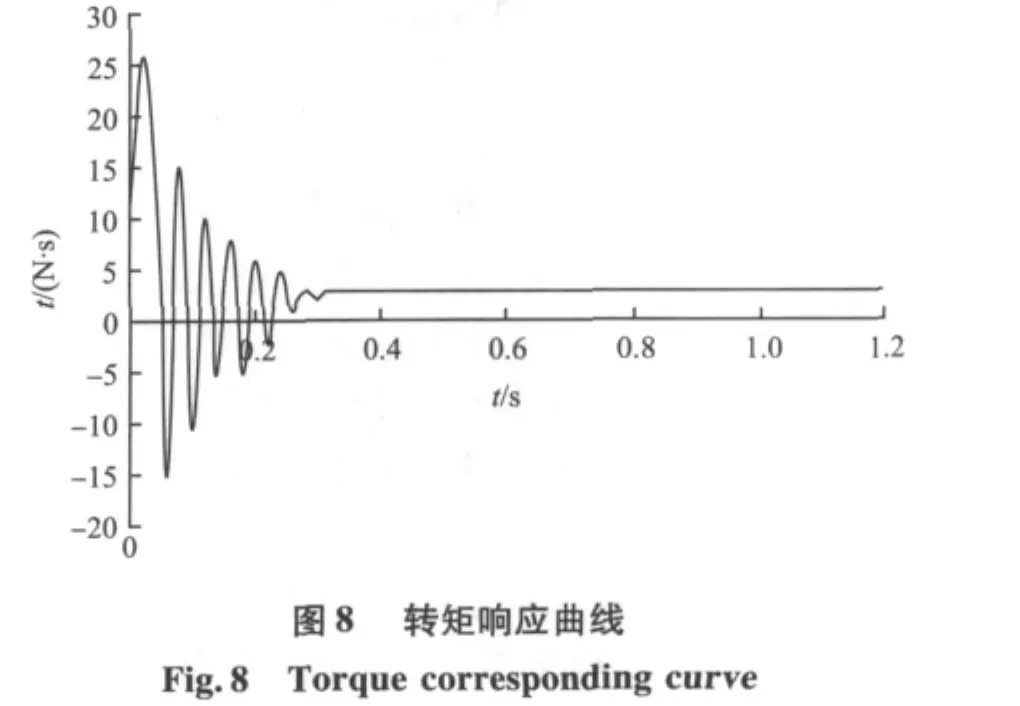
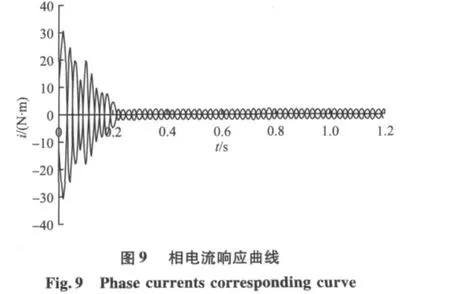
從轉速和轉矩響應曲線可以看出,轉速和轉矩在很短的時間內就達到了穩定值,雖然有輕微波動,但不影響整個系統。相電流曲線開始時電流值比較大,但很快達到設定值。通過仿真結果可以看出,系統能平穩運行,具有較好的靜、動態特性。
4 結語
針對永磁同步電機系統進行研究,運用虛擬參考迭代整定方法(FRIT)整定PID控制器參數,最后在Matlab/Simulink仿真下證明系統的擾動性能得到了很大的改善,并且由PMSM的轉速、轉矩、相電流等的仿真曲線圖看出系統能快速穩定,具有較好的靜、動態特性。通過仿真可知,當對象模型或者周期信號未知的情況下,正確運用FRIT方法能使問題得到很好的解決。
[1]Hjalmarsson H,Gevers S M.Gunnarsson,Lequin O.Iteretive feedback tuning:theory and applications[J].IEEE Control Systems Magazine,1998,18:26-41.
[2]Ogawa M,Kano M.Practice and challenges in chemical process control applications in Japan[C]//IFAC World Congress.Seoul,Korea:[s.n.],2008:10608-10613.
[3]Kaneko O,Yoshida K,Matsumoto K,et al.A new parameter tuning for controllers based on least-squares method by using one-shot closed loop experimental data an extension of fictitious reference iterative tuning[J].Trans of Institute of Systems,Control,and Information Engineering,2005,18(11):400-409.
[4]Campi M C,Savaresi S M.Direct nonlinear control design:the virtual reference feedback tuning(VRFT)approach[J].IEEE Trans On Auto matic Control,2006,51(1):14-27.
[5]陳宗云.基于DSP的永磁同步電機伺服系統的研究[D].杭州:浙江工業大學,2006.
[6]繆天舒,王隆太,許曉峰.基于重復控制的數控系統伺服調節技術的研究[J].機械科學與技術,2008,6(27):838-840.
MIAO Tian-shu,WANG Long-tai,XU Xiao-feng.Repeat the numerical control system based on control servo regulation technology[J].Mechanical Science and Technology,2008,6(27):838-840.(in Chinese)
[7]馬訓鳴,林曉煥.模型參考和重復控制在電液伺服同步加載系統中的應用研究[J].機床與液壓,2009,10(37):178-180.MA Xun-ming,LIN Xiao-huan.Model reference and repeat electro-hydraulic servo control in the application of synchronous loading system[J].Machine Tool and Hydraulic Pressure,2009,10(37):178-180.(in Chinese)
[8]白華煜,劉軍,楚小剛.基于模糊控制永磁同步電機直接轉矩控制研究[J].電氣傳動,2005,35(5):6-9.
BAI Hua-yu,LIU Jun,CHU Xiao-gang.Based on the fuzzy control permanent magnet synchronous motor direct torque control study[J].Electric Transmission,2005,35(5):6-9.(in Chinese)
[9]張立強.基于自適應模糊PID的徑向柱塞變量泵電液伺服控制[D].蘭州:蘭州理工大學,2003.
[10]王春行.液壓伺服控制系統(第2版)[M].北京:機械工業出版社,1993.

