港口船舶牽引機械強度及穩定性分析
韓 龍, 錢 怡
(江南大學機械工程學院,江蘇無錫214122)
船舶牽引機械是中大型港口常用的港口設備,其作用在于拉動貨船沿岸邊平行移動,便于裝卸貨物。由于該機械屬懸臂細長結構,其強度、剛度和穩定性決定牽引機械的工作可靠性和安全性,在結構設計時,必須分析滿載時結構的強度、剛度和穩定性。因此,正確的設計過程是給出結構的初步設計方案→運用有限元軟件ANSYS Workbench仿真平臺建立船舶牽引機械的整體結構有限元模型,并對其進行靜力分析→獲取結構在靜載作用下的應力變形分布→對整體結構進行穩定性分析→根據分析結果,改進設計方案并進行優化。
文中在靜力分析的基礎上,對牽引機械進行穩定性求解,同時參照相關起重機設計規范,對于機構的初步設計方案進行合理性評估。
1 船舶牽引機械有限元模型的建立
1.1 牽引機械三維實體模型
船舶牽引機械的金屬結構主要包括塔頂、起重臂架、平衡臂、滑輪組、絞車以及回轉支承等組成。其中起重臂架上弦桿為φ168×12規格的無縫鋼管,下弦桿為兩根180×180×14的方管,腹桿為φ63×9規格的無縫鋼管,拉索為φ25鋼纜。根據設計意圖及尺寸在PRO/E里建立船舶牽引機械初步的三維實體模型,如圖1所示。

圖1 牽引機械三維實體模型Fig.1 3D solid model of boat-haulage machine
1.2 牽引機械的有限元模型
1.2.1 建模原則及模型簡化 根據起重機設計規范的規定,建立起重機結構幾何模型過程中,忽略結構阻尼,不考慮非線性關系和過渡圓角[1]。為使有限元建模更加合理,結構模型化時重點關注了以下幾點:模型能全面準確地反映整機結構特點;模型受力與實際結構在工作時的外載荷相同;模型的邊界條件處理與牽引機械實際工作時的外部約束和部件間的銜接情況保持一致。牽引機械在有限元建模時,根據實際情況進行必要簡化[2]。
1)回轉支承簡化:由于回轉支承等實體部件相對結構整體而言幾何尺寸較小,剛度大,質量集中,且實體部分局部不易失穩,在整機結構穩定性分析時將回轉支承等實體部件采用質量等效處理[3]。
2)起重臂簡化:起重臂根部通過銷軸與回轉支承相連,由于起重臂根部鎖緊裝置的作用,因而回轉支承對起重臂的作用可用固定支座描述。起重臂與二根拉索的連接及拉索與塔頂的連接,均按固定鉸支座處理[4]。
3)牽引機械附件簡化:滑輪、絞車等附件由于相對整體結構而言幾何尺寸小,質量集中,對整體結構進行靜力和穩定性分析時,將附件等實體部件均采用等效剛體質量處理,其所受載荷以集中力方式加載于其與臂架的連接件之上。根據圣維南原理,這種處理僅影響附件作用點附近的局部應力大小及分布,對結構整體應力變化及分布無大的影響[5]。對于等截面部件,自重均按長度方向的均布載荷處理。
1.2.2 單元選擇 牽引機械起重臂架實體部分采用三維實體單元SOLID186,而拉索則采用LINK180單元。由于Workbench平臺不支持自主定義單元類型,通過Workbench平臺中的DM模塊建立線體模型并賦予截面特征參數,并在Mechanical模塊中插入Command命令以實現對拉索的模擬。附件質量以Point Mass附加于臂架相關位置模擬。
1.3 邊界條件的確定與載荷處理
鑒于工作時起重臂根部固定,該處設為固定約束,即線位移 Ux=0,Uy=0,Uz=0;角位移ROTx=0,ROTy=0,ROTz=0。塔頂以等效剛體質量處理,采用固定耦合的方式表示與之相連的拉索。
牽引機械所受載荷主要為自重、牽引載荷及風載荷等。為保證設計計算的可靠性與合理性,牽引機械的計算載荷選用最不利工況時的載荷組合:自重為分布力;牽引載荷以廠家提供數值施加;風載以分布力的形式作用于塔機側面,其數值一般按六級風壓設定,計算風壓 Pw2=250 Pa[6]。
1.4 有限元模型的建立
將PRO/E中建立的三維實體模型通過相關接口導入到ANSYS Workbench平臺,根據現行規范及上述處理建立有限元模型。按桿件材料規格型號和不同的截面劃分單元網格。結構材料特性如表1所示。

表1 材料特性Tab.1 Material properties
起重臂的網格劃分以六面體單元為主,輔以一定數量四面體及楔形單元。桿件之間連接定義為Bonded接觸以模擬焊接,銷釘件和與之相連部件之間的連接定義為Frictionless接觸。結構阻尼忽略不計,最終得到整機有限元模型如圖2所示(滑輪、絞車等部件均已按前文所述簡化原則作等效處理),共2 125 295節點,372 435單元。

圖2 結構有限元模型Fig.2 Finite element model of the structure
2 船舶牽引機械強度分析
由經典力學理論可知,結構的靜力學方程[7]
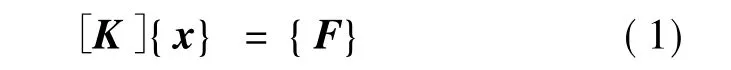
其中:[K]為剛度矩陣;{x}為位移矢量;{F}為力矢量。
由彈性力學給出應變位移關系及物理關系可得
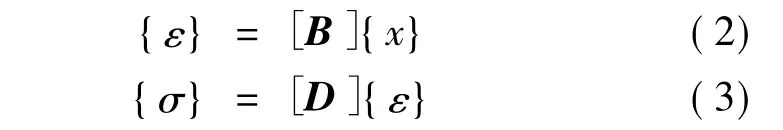
式中:[B]為應變矩陣;[D]為彈性矩陣。
通過式(1)求得結構位移,由式(2),(3)獲得相應的應力σ和應變ε數值。
設備的最大設計水平牽引載荷為20 kN,牽引纜繩與水平方向最大夾角為53°。通過對有限元模型求解,結構應力變形分布情況如圖3,4所示(44倍率)。
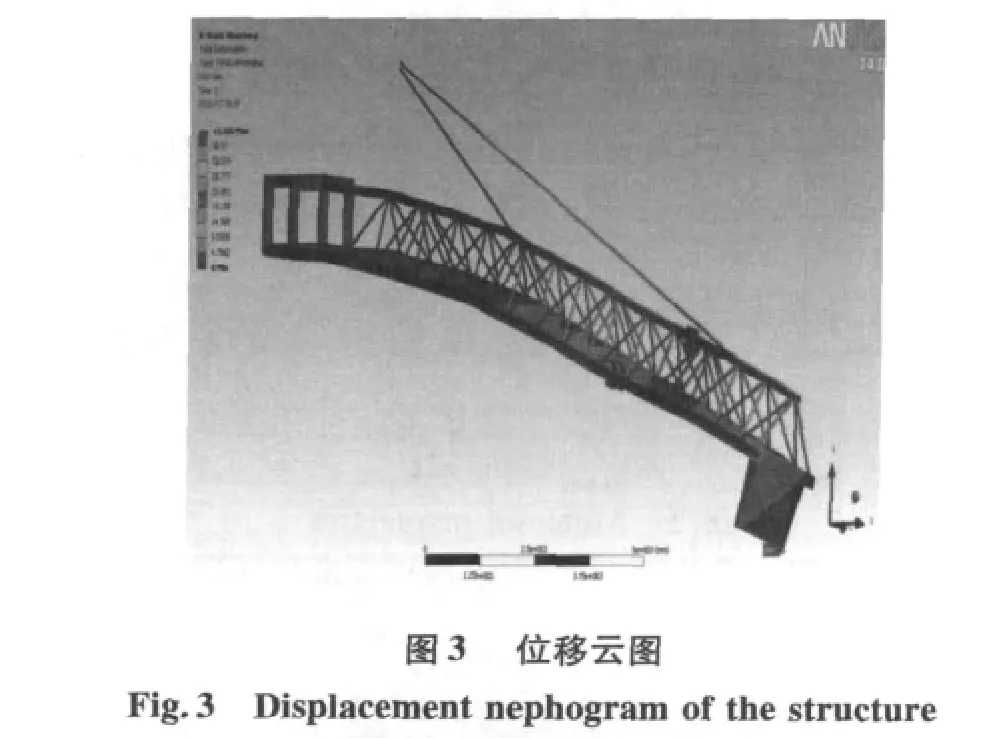

由圖3,4可知,牽引機械的最大位移出現在起重臂的端部,豎向最大位移為32.36 mm,總體最大位移為43.166 mm。牽引機械的變形主要來自牽引荷載,由于橫向風載作用,機身同時伴隨橫向彎曲,另外因牽引載荷中存在橫向分力,起重臂截面略有扭轉變形。
整機最大應力出現在起重臂根部附近,即與回轉支承銜接處,Von Mises最大等效應力為179.27 MPa。此外,拉索吊點附近及牽引載荷一側的下弦桿上,也有較大應力分布。
分析結果表明,最大應力值小于材料許用拉應力[σ]=345 MPa和許用壓應力[σ]=510 MPa。最大變形小于《起重機設計手冊》所規定的剛度要求,即吊臂懸臂撓度f≤4L/1 000。其中L為起重臂軸向尺寸,本結構設計值L=22.04 m,可見初步設計方案滿足結構強度和剛度要求。
3 船舶牽引機械穩定性分析
結構的失穩破壞一般可分為平衡狀態分枝型失穩和極值點失穩兩種,當載荷達到一定數值時結構發生平衡狀態分枝型失穩,失穩的臨界載荷可以通過分枝平衡狀態的分析進行計算。ANSYS程序提供了特征值屈曲和非線性屈曲兩種分析方法,按照起重機設計規范,文中選擇特征值屈曲對牽引機進行穩定性分析[8]。
線性屈曲分析基于經典的特征值問題,為了引出特征值問題,首先求解線彈性前屈曲載荷狀態的載荷-位移關系:
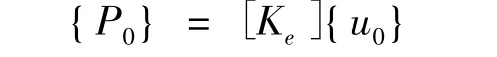
即給定{P0},求解上式中的位移{u0},同時可得應力{σ}。
假設前屈曲位移很小,在任意狀態下({P},{u},{σ})增量平衡方程由下式給出:
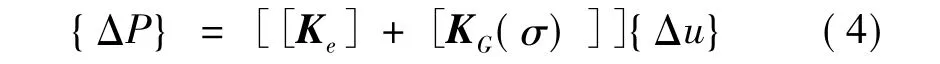
式中:[Ke]為彈性剛度矩陣;[KG(σ)]為某應力狀態{σ}下計算的幾何剛度矩陣。幾何剛度矩陣表示結構在變形狀態下的剛度變化,與施加的荷載有直接關系。任意構件受壓力時,剛度有減小傾向;反之,受拉力時,剛度有增大傾向。對三維實體單元幾何剛度矩陣
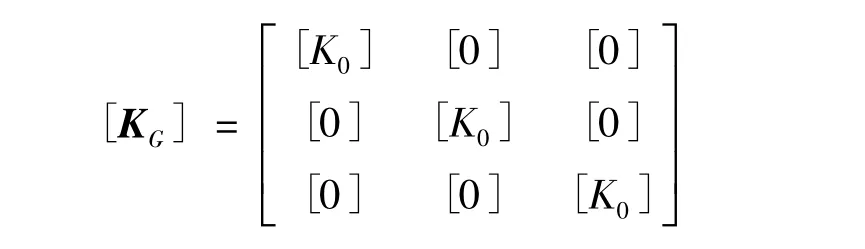
其中

式中,Ni為第 i節點的形函數[9]。
假設前屈曲行為是一個外加載荷{P0}的線性函數
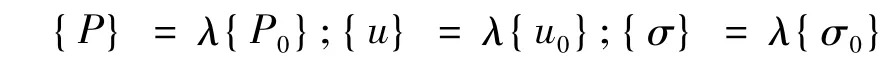
則可得
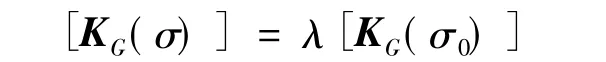
而式(4)變為
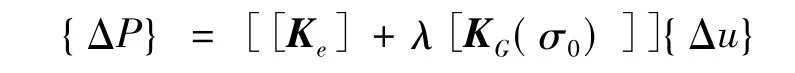
在不穩定開始時(屈曲載荷Pcr),{ΔP}=0,存在非零位移增量{Δu},故此時增量平衡方程變為
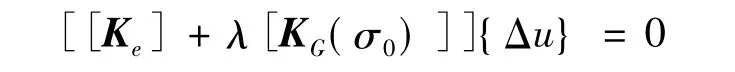
上述關系代表經典特征值問題,若結構處于不穩定狀態,平衡方程必有特殊解,即
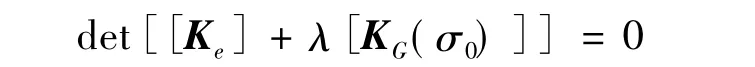
在n自由度的有限元模型中,上述方程產生λ(特征值)的n階多項式,特征向量{Δu}n表示屈曲時疊加到系統上的變形,由計算出的λ最小值給定彈性臨界載荷{Pcr}=λ{P0}。
依據上述原理,在靜力分析的基礎上,將相關數據傳遞到線性屈曲模塊(Linear Buckling),設置提取一階屈曲模態并求解。屈曲變形結果如圖5(2.2×109倍率)所示,載荷系數為26.366,實際載荷值34.3 kN,小于臨界載荷值904.3 kN,牽引機械滿足穩定性要求。

圖5 屈曲變形Fig.5 Buckling deformation of boat-haulage machine
4 結語
基于三維建模軟件PRO/E及有限軟件ANSYS Workbench平臺的無縫協同建模,高效率的建立了牽引機械的有限元模型,并對牽引機械的變形、各部分的應力及結構穩定性進行了全面分析,直觀得到機械的應力和變形分布及失穩位置,驗證了初步設計方案的合理性,也為機械的進一步優化打下了基礎,充分體現了這種分析思路在現代設計中的重要價值。
[1]《起重機設計手冊》編寫組.起重機設計手冊[M].北京:機械工業出版社,1980.
[2]陳瑋璋,顧迪民.起重機械金屬結構[M].北京:人民交通出版社,1985:7-56,216-240.
[3]楊長驥.起重機械[M].北京:機械工業出版社,1982:1-11,42-59,371-376.
[4]于蘭峰.塔式起重機結構剛性及動態優化研究[D].成都:西南交通大學,2007.
[5]王仿,高頂.塔式起重機整體結構的有限元分析[J].煤礦機械,2009,30(2):43-46.
WANG Fang,GAO Ding.Static finite element analysis of whole structure of tower crane[J].Coalmine Machinery,2009,30(2):43-46.(in Chinese)
[6]張青,劉青峰,王玉玲,等.基于三維實體模型的塔式起重機鋼結構設計[J].起重運輸機械,2006(7):27-29.
ZHANG Qing,LIU Qing-feng,WANG Yu-ling,et al.Design of tower crane steel structure based on 3D solid model[J].Hoisting and Conveying Machinery,2006(7):27-29.(in Chinese)
[7]蒲廣義.ANSYS Workbench 12基礎教程與實例詳解[M].北京:中國水利水電出版社,2010:65-70,178-193.
[8]鄭夕健,謝正義,張國忠.基于ANSYS的塔式起重機結構穩定性分析[J].建筑機械,2007(11):76-78.
ZHEN Xi-jian,XIE Zheng-yi,ZHANG Guo-zhong.The stability of the tower crane based on ANSYS[J].Construction Machinery,2007(11):76-78.(in Chinese)
[9]Peter Kohnke.ANSYS Inc Theory[M].Canonsburg:ANSYS Inc.,2011:68-74.

