奇素數函數及應用

李明玉

(渭南市氣象局，陜西渭南714000)

1 奇素數函數V(u)

定義1 如果 U={u|u∈Z，且u≠0，u≠－4ab+a － b，u≠4ab－ a － b，u≠4ab+a+b，a，b∈N}，則

稱作奇素數函數，u稱作奇素數函數變量.

定理1 給出函數變量 u，u∈Z，如果u≠0，u≠－4ab+a－b，u≠4ab－a－b，u≠4ab+a+b，a，b∈N，則函數的值域構成奇素數全集.

證明 設f(x)=︱4x+1︱為奇數函數，x∈z.

首先證明f(x)=︱4x+1︱包含了所有的奇素數.

當x=0時，f(x)=|4x+1|=1，即它既不是合數，也不是素數;

當x＞0時，f(x)=|4x+1|?f(x)=4x+1;

當x＜0時，f(x)=|4x+1|?f(x)=4×|x|－1.

設N是正整數，則

N ≡1(mod 4)，N=4x+1;

N≡2(mod 4)，N是偶數，其中只有2是素數;

N≡3(mod 4)，N=4x－1;

N≡0(mod 4)，N沒有素數，是偶合數.

由此可見，所有的奇素數都包含在奇數函數f(x)=|4x+1|之中，無一例外.

下面證明，若x∈ Z，x≠0，x≠－4ab+a － b，x≠4ab－ a － b，x≠4ab+a+b，a，b∈N，則f(x)=|4x+1|都是奇素數.

設 f(x)=|4x+1|是奇合數，x≠0，則 ?y1，y2∈ N，使 f(x)=|4x+1|=y1y2.

由于f(x)為奇數，所以y1，y2均為奇數，即?a，b∈N，使得y1=4a+1或者4a－1;y2=4b+1或者4b－1.

由于a，b的任意性，所以f(x)=|4x+1|=y1y2只能是下面三種情況之一:

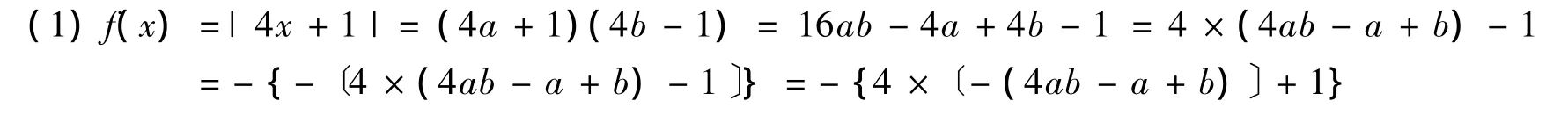
所以，如果f(x)=|4x+1|為合數，則x的值只能為x=－4ab+a－b，或x=4ab+a+b，或x=4ab－ a － b.也就是說，若 x∈ Z，x≠0，x≠－4ab+a － b，x≠4ab－a － b，x≠4ab+a+b，a，b∈N，則f(x)=|4x+1|都是奇素數.

因為u∈Z，u≠0，u≠－4ab+a－b，u≠4ab－a－b，u≠4ab+a+b，所以，函數V(u)= ︱4u+1︱既沒有1和奇合數，又包含了所有的奇素數.因此，V(u)=︱4u+1︱的值域是奇素數全集.

2 簡化素數函數V(m)

定義2 如果m={m|m∈Z，且m≠0，m≠－6ab+a－b，m≠6ab－a－b，m≠6ab+a+b，a，b∈ N}，則

稱作簡化素數函數，亦稱作不小于5的素數函數，m稱作簡化素數函數變量.

雖然函數V(m)比奇素數函數V(u)少了奇素數3，但在使用中就方便多了.與奇素數函數V(u)相比，簡化素數函數V(m)在函數值域相同的情況下，其函數變量的定義域的取值范圍卻顯著縮小，因此，在實際計算中，工作量明顯減少，數字越大越明顯.所以，將函數(2)稱作簡化素數函數.

定理2 給出函數變量m，m∈Z，如果m≠0，m≠－6ab+a－b，m≠6ab－a－b，m≠6ab+a+b，a，b∈ N，則函數的值域是不小于5的素數集合.

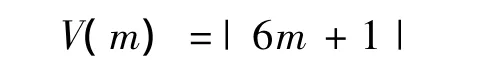
證明 設f(x)=|6x+1|是奇數函數，x∈Z.

首先證明f(x)=|6x+1|，包含了除2和3之外的所有素數.

當x=0時，f(x)=|6x+1|=1，即它既不是合數，也不是素數;

當x＞0時，f(x)=|6x+1|?f(x)=6x+1;

當x＜0時，f(x)=|6x+1|?f(x)=6×|x|－1.

設N是正整數，則

N ≡1(mod 6)，N=6x+1;

N≡2(mod 6)，N是偶數，其中只有2是素數;

N≡3(mod 6)，N是能被3整除的數，其中只有3是素數;

N≡4(mod 6)，N是偶數，都是合數;

N≡5(mod 6)，N=6x－1;

N≡0(mod 6)，N沒有素數，是偶合數.

由此可見，除了2和3外，奇數函數f(x)=|6x+1|包含了其余所有的素數.

下面證明，若x∈ Z，x≠0，x≠－6ab+a － b，x≠6ab－ a － b，x≠6ab+a+b，a，b∈N，則f(x)=|6x+1|都是奇素數.

設 f(x)=|6x+1| 是合數，x≠0，則 ?y1，y2∈ N，使 f(x)=|6x+1|=y1y2.

由于f(x)為奇數，所以y1，y2均為奇數，即?a，b∈N，使得y1=6a+1，或6a－1，或6a+3;y2=6b+1，或6b － 1，或6b+3.

又由于f(x)=|6x+1|=y1y2是不存在素因子3的奇數，因此，y1，y2均不可能為6a+3和6b+3.

所以y1=6a+1或6a－1;y2=6b+1或6b－1.

由于a，b的任意性，所以f(x)=|6x+1|=y1y2只能是下面三種情況之一:

所以，如果f(x)=|6x+1|為合數，則x的值只能為x=－6ab+a－b，或x=6ab+a+b，或x=6ab－ a － b.也就是說，若 x∈ Z，x≠0，x≠－6ab+a － b，x≠6ab－a － b，x≠6ab+a+b，a，b∈N，則f(x)=|6x+1|都是大于3的奇素數.

由于奇數函數f(x)=|6x+1|包含了除2和3之外的全部素數.又因為m∈Z，m≠0，m≠－6ab+a－b，m≠6ab+a+b，m≠6ab－a－b，所以，函數V(m)=|6m+1|既沒有1和合數，又包含了除2和3之外的全部素數.因此，V(m)=|6m+1|的值域是不小于5的素數集合.

3 應用

3.1 求素數判別函數f(b)

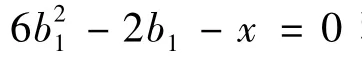
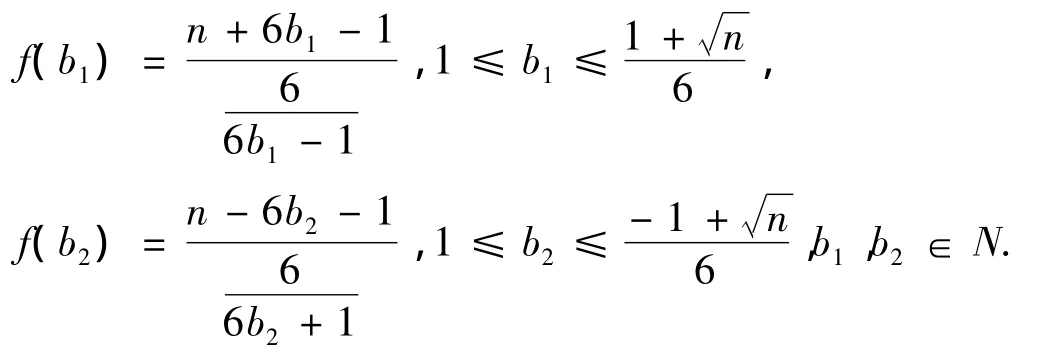
若函數f(b)的值都不是整數時，則n就是素數，否則就是合數.

例1 用判別函數識別299是素數還是合數.

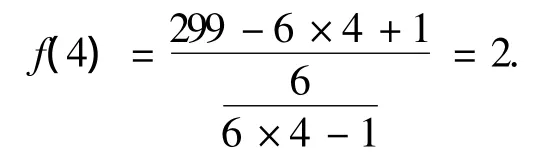
因為判別函數值是整數，所以299是合數，299=13×23.

例2 用判別函數識別253是素數還是合數.

因為判別函數值是整數，所以253是合數，253=11×23.

3.2 求素數及個數

例3 求51到100內的素數和素數個數.

解 在函數V(u)=︱4u+1︱中，

1

若u1=－4ab+a－b，有 －25≤－4ab+a－b≤－13，即

而u1≠－4ab+a－b，所以{u1}={－15，－17，－18，－20，－21}.

2

若u2=4ab－a－b和u2=4ab+a+b，有 13≤4ab－a－b≤24，13≤4ab+a+b≤24，即

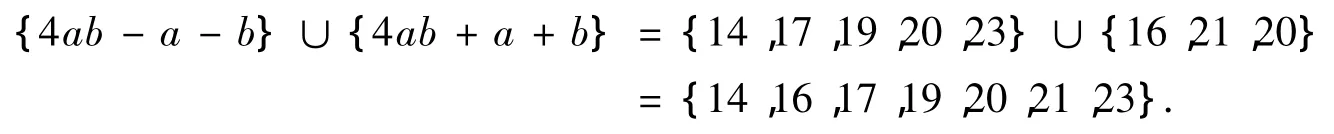
而 u2≠ 4ab － a － b，u2≠4ab+a+b，所以{u2}={13，15，18，22，24}.

所以{u}={u1}∪ {u2}={－15，－17，－18，－20 －21}∪ {13，15，18，22，24}={－ 15，－ 17，－ 18，－ 20，－ 21，13，15，18，22，24}.

所以n(U)=10.

將素數函數變量代入V(u)=|4u+1|，得:

例4 求9951到10000內的素數和素數個數.

解 設素數函數為V(m)=|6m+1|，M為素數函數變量m的集合，M補為素數函數變量集合的補集，則M補={－6ab+a－b}∪{6ab－a－b}∪{6ab+a+b}.

若m1=－6ab+a－b，則 －1666≤－6ab+a－b≤－1659，(這時設m1∈M補1).

當a=b時，－6ab+a－b=－6a2≥－1666，有 a≤16.同理可得:b≤16.

當a=1時，－1666≤－6b+1－b≤－1659，即238≥b≥238，則有

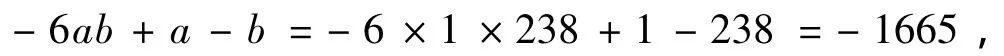
當a=2時，－1666≤－6×2b+2－b≤－1659，即128≥b≥128，則有

…

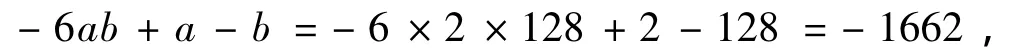
同理可得:

若 m2=6ab－a－b，m2=6ab+a+b，則1659≤6ab－a－b≤1666，1659≤6ab+a+b≤1666(這時設m2∈M補2).

當a=b時，6ab－a－b=6a2－2a≤1666， 6ab+a+b=6a2+2a≤1666.即

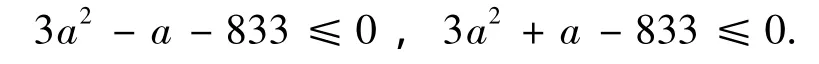
解得:

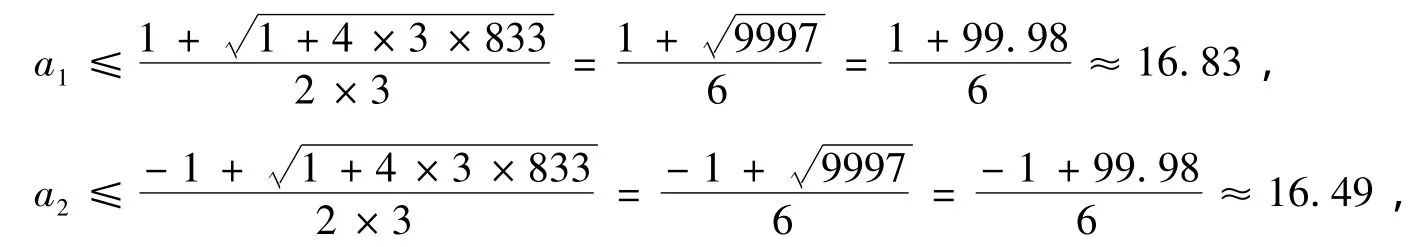
所以a≤16.

由于6ab－a－b和6ab+a+b都是對稱函數，所以a和b是同型項，b不需計算.

當a=1時，1659≤6b－1－b≤1666，即 332≤b≤333.

1659≤6b+1+b≤1666，即237≤b≤237.

所以6ab－a－b=6×1×332－1－332=1659，6ab－a－b=6×1×333－1－333=1664，6ab+a+b=6×1×237+1+237=1660，

…

同理可得:

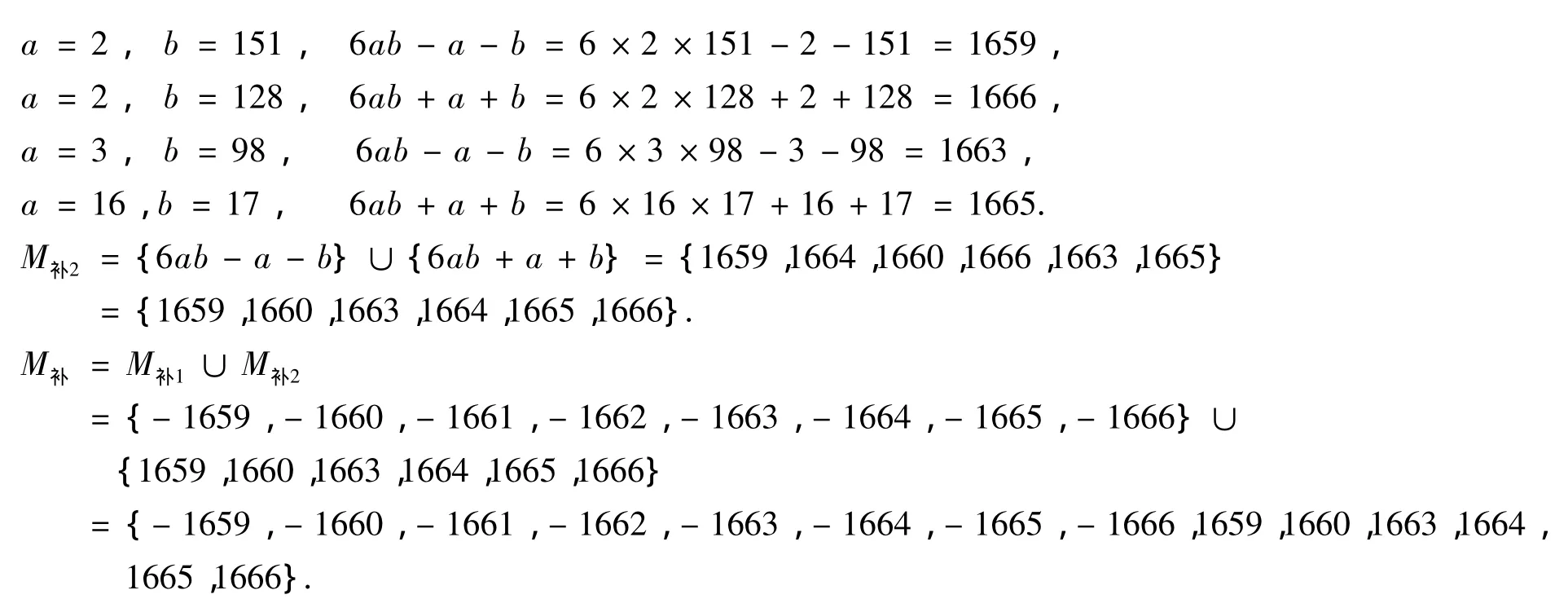
則 M={1661，1662}.

所以n(M)=2.

所以從9951到10000內的素數為{9967，9973}，共2個.

3.3 梅森素數的素數函數F(p)

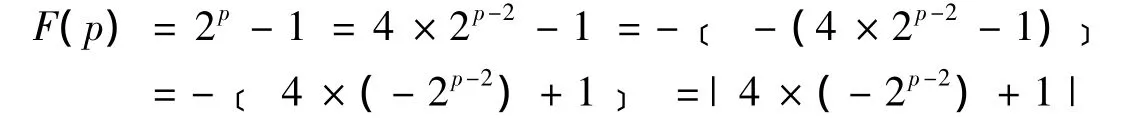
因為 － 2p－2≤－ 1，即2p－2≥1，所以 p ≥2.

又因為 － 2p－2≠－ 4ab+a － b，即2p－2≠4ab － a+b，有2p≠16ab － 4a+4b.

所以p≠log2(16ab－4a+4b)=2+log2(4ab－a+b).

所以梅森素數的素數函數是:F(p)=2p－1，其中p≥2，p≠2+log2(4ab － a+b)，a，b≥1，a，b∈N.

3.4 高斯素數的素數函數F(u)

所謂高斯素數，就是在奇素數函數V(u)=︱4u+1︱中，素數函數變量為負整數的一類素數.高斯素數是在復數域中仍不能分解的一類素數.這類素數形如4u－1.

因為F(u)=4u－1=－﹝ －(4u－1)﹞ =－﹝4×(－u)+1﹞ =|4×(－u)+1|，而 －u≤－1，即 u ≥1.

又因為 －u≠－4ab+a－b，即u≠4ab－a+b.

所以高斯素數的素數函數是:F(u)=4u － 1，其中 u≥1，u≠4ab － a+b，a，b≥1，u，a，b∈ N.

3.5 形如 s2+1的素數函數F(s)

在二次式s2+1中，當s是奇數時，s2+1是偶數，其中，只有s=1時，s2+1是素數2，其余都是合數.所以，素數s2+1中的奇數變量不是變量，而是常量1;當s是偶數時，s2+1是奇數，所以，s2+1既有合數，也有素數.因此，素數s2+1的變量s是偶數，不是奇數.因而，s2能被4整除.

又因為s是偶數，所以s≤－2n或s≥2n，n∈N.

所以s2≠4×(4ab－a－b)， s2≠4×(4ab+a+b)，

因為此函數的變量都是偶數，所以，我們將它稱作偶變量素數函數F(s).

3.6 孿生素數的素數函數F(mr)

所謂孿生素數是指差為2的相鄰素數.

當素數函數變量m1＞0時，則其素數p1可表示為p1=6m1+1.

當素數函數變量m2＜0時，則其素數p2可表示為

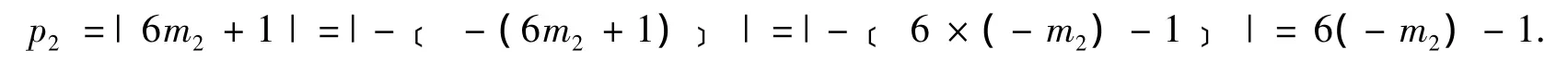
如果m1=－m2，則p1－p2=(6m1+1)－﹝6×(－m2)－1﹞

這說明了當素數變量m1=－m2時，則其素數就是一對孿生素數.

設 m1，m2，mr都是素數函數變量，m1≥ 1，m2≤－ 1，mr=m1= － m2，則 mr≥ 1.

因為m1≠6ab－a－b， m1≠6ab+a+b，所以mr≠6ab－a－b， mr≠6ab+a+b

又因為m2≠－6ab+a－b，所以mr≠6ab－a+b.

所以孿生素數的素數函數是:F(mr)=6mr±1.其中 mr≥1，mr≠6ab－a－b，mr≠6ab+a+b，mr≠ 6ab － a+b，a，b ≥1，mr，a，b ∈ N.

3.7 費馬素數的素數函數F(k)

設 n=2k，則 F(k)=2n+1=2n+1+1 － 1=2 × (2n－1+1)－ 1.

因為n=2k，所以n－1是奇數，2n－1+1能被3整除.

又因為n=2k，所以k≥1，k∈N.

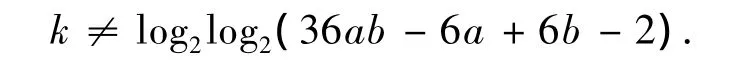
所以費馬素數的素數函數可以表示為:

3.8 艾森斯坦素數的素數函數F(n)

數學家艾森斯坦也定義了一種素數:形如n+mω的數被稱為艾森斯坦整數，而艾森斯坦素數則是艾森斯坦整數的一個子集.這類素數都是除以3余2的素數，除了2不可以用函數表示外，其余素數都可以用6n－1來表示.

因為F(n)=6n－1=－﹝6×(－n)+1﹞ =|6×(－n)+1|，所以艾森斯坦素數，除了2，其余素數都是簡化素數函數V(m)=|6m+1|中變量為負整數的一類素數.

因為 －n≤－1，所以n≥1，又因為 －n≠－6ab+a－b，所以n≠6ab－a+b.所以艾森斯坦素數，除了2，都可以用下列函數表示:

3.9 等差素數的變量是等差數列

設素數 p1，p2，p3是等差數列，則 p2－ p1=p3－ p2.

當素數函數變量mi≥1時，有 p1=6m1+1，p2=6m2+1，p3=6m3+1.

因為p2－p1=p3－p2，所以6×(m2－m1)=6×(m3－m2)，即m2－m1=m3－m2.

當素數函數變量 mi≤－1時，p1=|6m1+1|=－6m1－1，p2=|6m2+1|=－6m2－1，p3=|6m3+1|=－6m3－1.

因為p2－p1=p3－p2，所以6×(m1－m2)=6×(m2－m3)，即m1－m2=m2－m3.

這說明，當幾個素數是等差素數時，其素數函數的變量是等差數列.

3.10 形如q2+2的素數函數F(q)

由于F(q)=q2+2是素數，所以q是奇數.

當q≡1(mod 3)時，q2≡1(mod 3)，這時只有q=1時，q2+2是素數3，其余都是能被3整除的合數;

當q≡2(mod 3)時，q2≡1(mod 3)，這時q2+2全是能被3整除的合數;

當q≡0(mod 3)時，q2≡0(mod 3)，這時q2+2有素數也有合數.

所以形如q2+2的素數，除了q=1外，其它素數都出現在能被3整除的奇數q中，即q≡0(mod 3).

因為 －(q2+3)/6≤－1，所以q2≥3.

因為q都出現在能被3整除的奇數中，所以q≤－3×(2n+1)，q≥3×(2n+1)，n≥0，q，n∈Z.

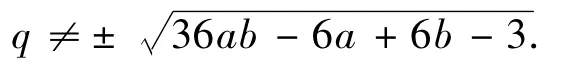
因為此函數的變量都是奇數，所以，我們將它稱作奇變量素數函數F(q).

4 結語

(1)素數除了2是偶數外，其余素數都是奇數.奇素數除了3之外，都分布在能被6整除的偶數的兩旁，即6k+1或6k－1.素數可以通過素數函數V(m)=|6m+1|和V(u)=|4u+1|進行計算.

(M，U 是素數函數變量集合，a，b≥1，a，b∈ N).

(2)素數分類的方法很多，最好的分類方法是以下兩種:

第一種是用奇數3進行分類:

i)3 3≡0(mod 3)

ii)6m+1 (6m+1)≡1(mod 3)(m是正整數)

iii)2和6|m|－1 (6|m|－1)≡2(mod 3)(m是負整數)

第二種是用偶數4進行分類:

i)4u+1 (4u+1)≡1(mod 4)(u是正整數)

ii)2 2≡2(mod 4)

iii)4|u|－1 (4|u|－1)≡3(mod 4)(u是負整數)

［1］潘承洞，潘承彪.初等數論［M］.第2版.北京:北京大學出版社，2003.

［2］閔嗣鶴，嚴士健.初等數論［M］.第3版.北京:高等教育出版社，2003.

［3］［美］羅森.初等數論及其應用［M］.夏鴻剛，譯.北京:機械工業出版社，2009.