對傍軸標量衍射理論的修正分析

安 博

(渭南師范學院物理與電氣工程學院，陜西渭南714000)

基爾霍夫衍射理論［1］借助數學中的格林定理求解亥姆霍茲方程得出.

格林定理［2］G，u為坐標系內的兩個任意復函數，S為包圍空間某體積V的封閉曲面.若u，G以及它們的一階導數、二階導數在S面內和面上都是單值連續的，則有:

設光場的光振動為u(p，t)，p點為觀察點，亥姆霍茲方程為:

只要選取合適的格林函數G，就可由格林定理和亥姆霍茲方程求出u(p).

1 基爾霍夫衍射理論的不自洽性

基爾霍夫選格林函數G(P0)為由P點向外發散的單位振幅的球面波，S面為包圍觀察點P的任意封閉曲面，在任意點P0上G的表示為:

r為觀察點P到P0的距離，為了排除P點的不連續性，必須把P點從討論的V內“挖出”，這樣G才能滿足格林定理的要求.為此我們作一以P點為中心，半徑為ε的小球面Sε，由格林定理和亥姆霍茲方程得到

(3)式稱為基爾霍夫積分公式.但由于邊界條件的不可知性，其實用性也受到了限制［3］.

研究無限大不透明平面上的小孔Σ所引起的衍射問題時，(3)式可以化簡為:

S1表示緊靠屏幕后的平面.要從(4)式中求出u(p)需要對邊界條件作如下假設:

(1)在Σ上各點，u和?u/?n的分布與屏不存在同時相同，即完全由入射光波在這里的光場決定;

(2)在不透明的屏表面上各點，u和?u/?n都等于0.

這時(4)式可以進一步簡化為:

(5)式表明，光波穿過具有透光孔Σ的無限大屏后，屏后空間任意點p的光波復振幅u(p)可以由孔上Σ的光場復振幅u(p0)及其法線方向的偏導數來表示.

雖然基爾霍夫衍射積分公式對于一般的衍射問題可以給出與實際符合得非常好的結果，但是，基爾霍夫理論本身存在明顯的不自洽性［4］.基爾霍夫邊界條件明確指出［1］，在屏后光場的復振幅及其法向導數均為0，但由電動力學中場論的基本原理可以證明，如果波動方程的一個解在任意非無限小的面元上光場的復振幅和它的法向導數都為0，則這個解在整個空間都為0，這個結論與實際情況相矛盾.

2 對基爾霍夫衍射理論不自洽性的修正

基爾霍夫衍射理論能夠給出與實驗符合較好的結果，但理論本身存在嚴重的不自洽性.而基爾霍夫衍射理論的不自洽性主要來自于同時對邊界上光場的復振幅及其法向導數施加邊界條件.為了克服基爾霍夫理論的不自洽性，可以通過提出格林函數的另一種選擇的方法，使得不必同時對邊界上光場的復振幅及其法向導數施加邊界條件，從而克服了基爾霍夫理論本身的不自洽性［5］.

選擇一種新的格林函數

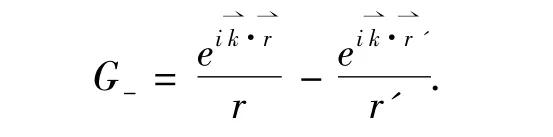
對于無限大不透明屏上一個小孔的衍射問題，格林函數由p點和p'點的函數共同產生.

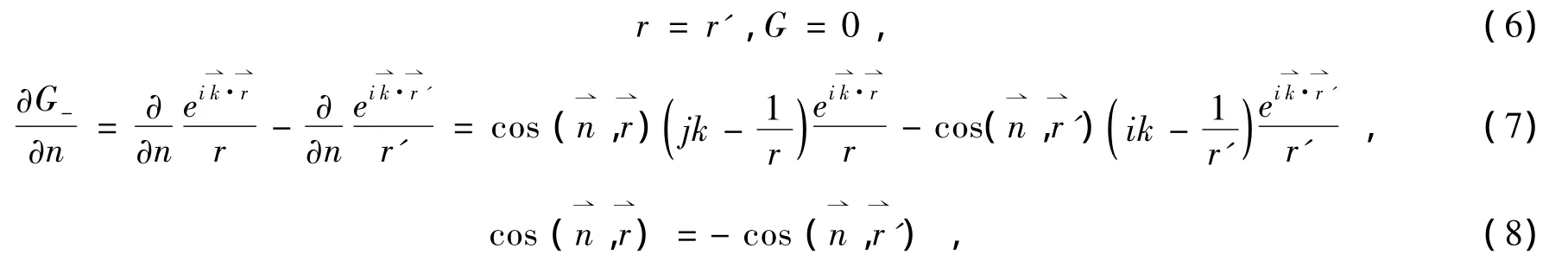
代入格林定理和亥姆霍茲方程，得到:

因此只需在積分面上對u(p0)施加邊界條件:

(1)屏后表面的u處處為0;

(2)孔Σ上的u與沒有衍射屏時相同.

于是(9)式簡化為:

G也可以有另一種選擇方式:

此式由兩個振動同向的格林函數線性組合而成，除此以外與G無異.對于無限大不透光屏上的小孔衍射，由格林定理和亥姆霍茲方程得到:

施加邊界條件:

與無屏相同.

此時僅u的導數消除了不自洽性:

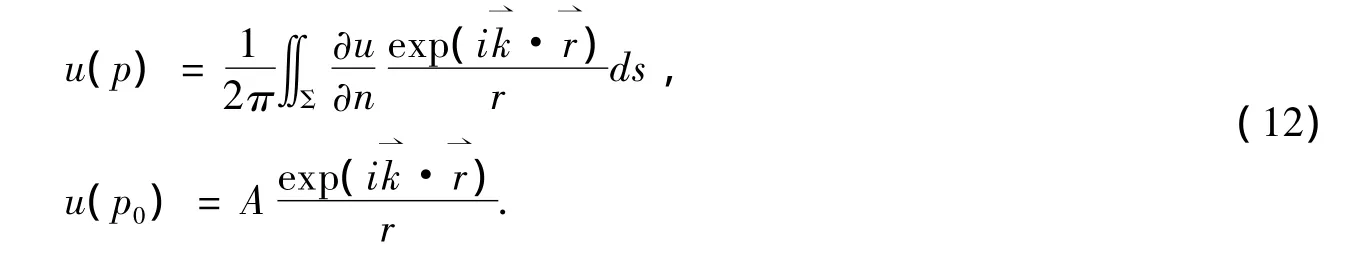
3 修正后的基爾霍夫衍射理論對雙縫衍射的應用

假如衍射孔徑位于x0y0平面，觀察點位于xy平面，觀察平面與孔徑平面的距離為z遠大于孔徑線度，單位振幅的平行光垂直入射衍射孔徑，孔徑上光場分布為

在傍軸近似下

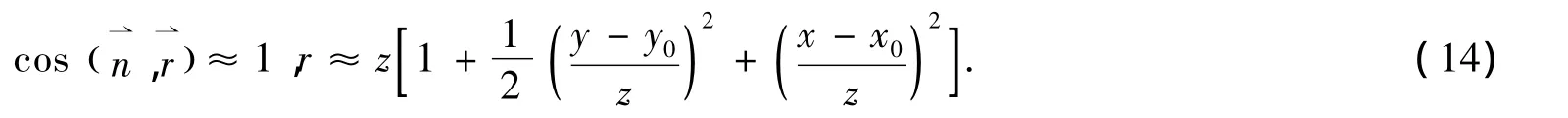
把(13)(14)式代入(10)式得:

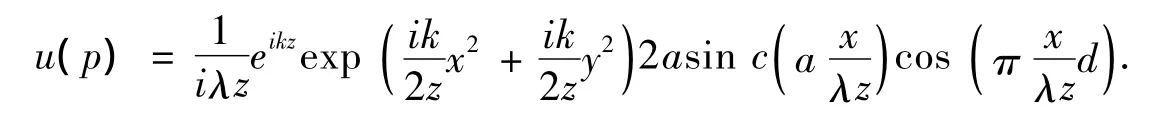
在傍軸近似下(10)式分母中r≈z.觀察面上光強分布為

這也正是基爾霍夫衍射理論應用于雙縫衍射的結果.

4 結語

［1］Born M，Wolf E.Principles of Optics［M］.London:Cambridge University Press，1999.430.

［2］郭碩鴻.電動力學［M］.北京:高等教育出版社，1997.101.

［3］鄧小玖，高峰，劉彩霞，等.標量衍射理論的非傍軸近似及其有效性［J］.光子學報，2006，35(6):898.

［4］梅妍.衍射理論中的佯謬［J］.遼寧師范大學學報(自然科學版)，1996，19(1):36－39.

［5］劉春香，程傳福，任曉榮，等.隨機表面散射光場的格林函數法與基爾霍夫近似的比較［J］.物理學報，2004，53(2):427－435.