惠斯通電橋測量楊氏模量的實驗探究

董康軍，田蘇陽

(渭南師范學院物理與電氣工程學院，陜西渭南714000)

楊氏模量是表征固體材料性質的一個重要的物理量，是材料的一個基本力學參數，僅僅取決于材料本身的物理性質，它的大小標志了固體材料的剛性［1］.由胡克定律指出，在彈性限度內，彈性體的應力和應變是成正比的.假設一段鋼絲的原長為L，橫截面積為S，沿長度方向施加力F后，其長度改變量為ΔL，則鋼絲單位橫截面積上所受到的垂直作用力F/S稱為正應力，鋼絲的相對伸長量ΔL/L稱為線應變［2－3］，即

則

比例系數E稱為楊氏模量，E越大的固體材料，要使它發生一定的相對形變則所需要的單位橫截面積上的作用力就越大.

楊氏模量的測定在科學研究和技術應用中具有重要意義.測定楊氏模量的方法有很多種，靜態拉伸法相對比較簡單，它利用了光杠桿的放大原理并結合望遠鏡測定鋼絲的微小伸長量，此方法直觀簡便，在物理實驗中經常被采用;惠斯通電橋法是通過創新思維而開拓的新實驗方法，是將鋼絲直接接入電橋中充當電阻，把鋼絲長度的變化通過電阻的變化表示出來，它結合了力學和電學知識，對知識的綜合運用讓實驗更具有探究性.本文重點研究惠斯通電橋法測量楊氏模量，對提高楊氏模量的測量精度具有重要的意義.

1 惠斯通電橋法測量楊氏模量

1.1 惠斯通電橋的工作原理

惠斯通電橋的原理圖如圖1所示，可以證明在電橋平衡時，有

若R1，R2及R3已知，則可求出待測電阻Rx為

通常R3和R1稱作比例臂，其比值稱作比率;R2為比較臂;而Rx稱為未知臂.在實際測量的電路中R1，R2和R3都可以用標準電阻和高精度的電阻箱，因此用惠斯通電橋測量電阻可以達到很高的準確度.

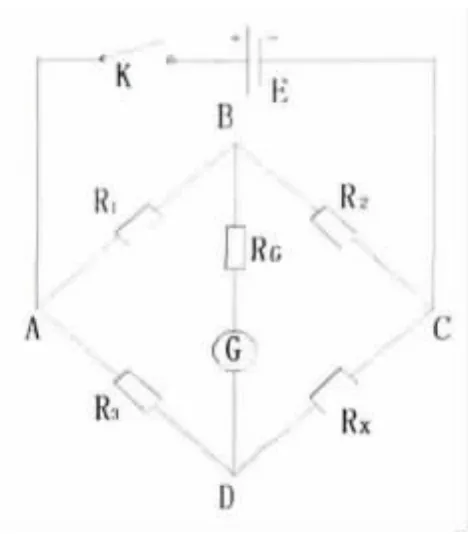
圖1 惠斯通電橋原理圖

當電橋達到平衡時，若使比較臂R1改變一個微小量ΔR1，則電橋將偏離平衡，靈敏檢流計將偏轉n個格，因此通常用如下的相對靈敏度s表示電橋的靈敏度［4－5］

靈敏檢流計的內阻越小，靈敏度越高，則電橋的靈敏度越高;橋臂的內阻越小，電橋的靈敏度越高，而當4個橋臂的阻值相等時，其靈敏度將接近最大值;在橋臂電阻功率許可的情況下，電源的電壓越高，電橋的靈敏度越高.

1.2 惠斯通電橋法測量楊氏模量實驗原理

惠斯通電橋法測量楊氏模量實驗裝置主要由三部分組成:楊氏模量測定儀、直流電橋和直流電源.將楊氏模量測定儀上的測量鋼絲上下兩端(兩個夾頭之間的部分)直接用銅芯導線接入直流電橋中充當待測電阻Rx，而惠斯通電橋和拉伸法測楊氏模量實驗儀器部分除去光杠桿系統外其它部分均保持不變.

當鋼絲伸長或收縮時，鋼絲的電阻Rx發生變化，R3和R1為比例臂，因此為保證惠斯通電橋的平衡，應調節比較臂R2的電阻，每加一個1 kg砝碼，記錄一次電阻箱的數值Rx.

當電橋處于平衡狀態時

則鋼絲的伸長量ΔL為

將F=mg和S=πd2/4、(7)(8)式代入(2)式，可以得出用惠斯通電橋法測量鋼絲的楊氏模量E的公式為

1.3 數據處理

實驗室環境溫度為25℃，金屬絲選擇鋼絲.鋼絲原長L=105.90 cm;鋼絲直徑d=0.4856 mm;鋼絲的電阻率 ρ=0.14 ×10－6Ω·m.

所以得到測量鋼絲的電阻計算值為R0=0.80093 Ω.

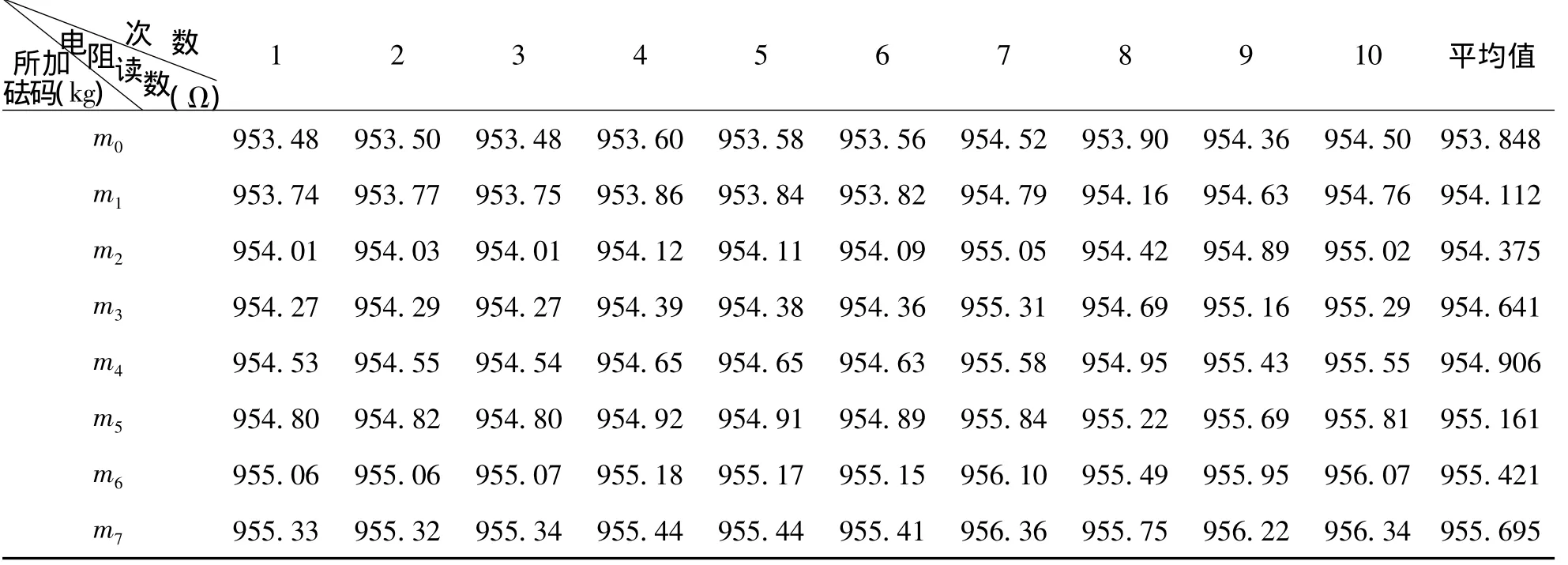
表1 加砝碼后電阻箱阻值R2數據表

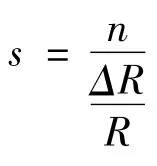
表2 逐差法計算ΔR的數據表

由公式(9)得計算公式

將測量數據代入公式(11)，得表3.

表3 楊氏模量的數據表

2 結語

同樣的條件下，重新用靜態拉伸法和本文惠斯通電橋法可得到鋼絲楊氏模量實驗值分別為18.7854×1010N/m2和19.1656×1010N/m2，即用惠斯通電橋法所測量的值與鋼絲楊氏模量的理論值20.1×1010N/m2更符合;并且通過計算得出用兩種方法測量的平均絕對誤差分別為1.3146和0.93433，平均相對誤差分別為6.54%和4.65%，相對不確定度分別為0.43%和0.32%，可以得出用惠斯通電橋法測量鋼絲的楊氏模量比用傳統拉伸法測量的精確度更高.通過實驗可知，惠斯通電橋法測定的鋼絲楊氏模量實驗由于不需要進行較為麻煩的光杠桿調節，所以可以更加方便快捷、間接測出鋼絲楊氏彈性模量.

［1］Pintelon R，Guillaume P，Vanlanduit S，et al.Identification of Young’s modulus from broadband modal analysis experiments［J］.Mechanical Systems and Signal Processing，2004，18(4):699 －726.

［2］吳俊林.基礎物理實驗［M］.北京:科學出版社，2010.

［3］漆安慎，杜嬋英.力學［M］.北京:高等教育出版社，2005.

［4］楊述武.普通物理實驗［M］.北京:高等教育出版社，2000.

［5］李麗霞，張秀.惠斯通電橋靈敏度的探討［J］.孝感學院學報，2004，24(6):67－68.