產品銷售預測的數(shù)學模型及應用

汪珊珊 李琳珊 程 翊 孟瑩哲

（杭州電子科技大學理學院，浙江 杭州 310000）

一、問題的背景與研究意義

預測之于工作與生活其實無處不在，同人民群眾的生活有著密切的聯(lián)系。不論是生活工作的安排還是企業(yè)計劃的制定，甚至是國家政策的訂立都會根據(jù)客觀存在的實際情況來做出決定，并根據(jù)這些條件來指導其行為，盡力去實現(xiàn)這個目標，同時努力地減少各種損失。在經濟不斷發(fā)展的今天，同時也伴隨著市場競爭性不斷增強的這樣一種情況下，企業(yè)為了達到所預期的經濟活動，更加需要使用歷史數(shù)據(jù)來進行判斷和分析，并依據(jù)這些判斷和分析的結果來制定出未來的營銷、生產計劃。而這個過程就需要對數(shù)據(jù)進行定量的分析之后做出預測，將預測結果作為制定這些計劃的有效依據(jù)。

預測是決策的重要憑據(jù)，也是決策的先決條件。預測利用對歷史的分析來掌握更豐富的未來信息。對任何事物來說，過去、現(xiàn)在和未來是相互關聯(lián)的，過去的存在對現(xiàn)狀產生影響，而現(xiàn)狀如何又會對將來產生影響。掌握了這種發(fā)展規(guī)律，才能更好地進行決策，使事物順應預期的發(fā)展。

本文根據(jù)已有的銷售數(shù)據(jù)，建立產品的銷售量預測模型及產品相互關聯(lián)性分析模型，為企業(yè)制定最優(yōu)的生產方案，促進企業(yè)的良好發(fā)展。

二、模型的假設與符號說明

（一）合理假設

1.不考慮消費者的需求動向及同業(yè)競爭動向帶來的影響。

2.忽略經濟政策變動及消費者導向的影響。

3.生產商的銷售策略不變，市場、生產狀況穩(wěn)定。

4.同一種產品不考慮其型號的不同帶來的影響 。

（二）符號說明

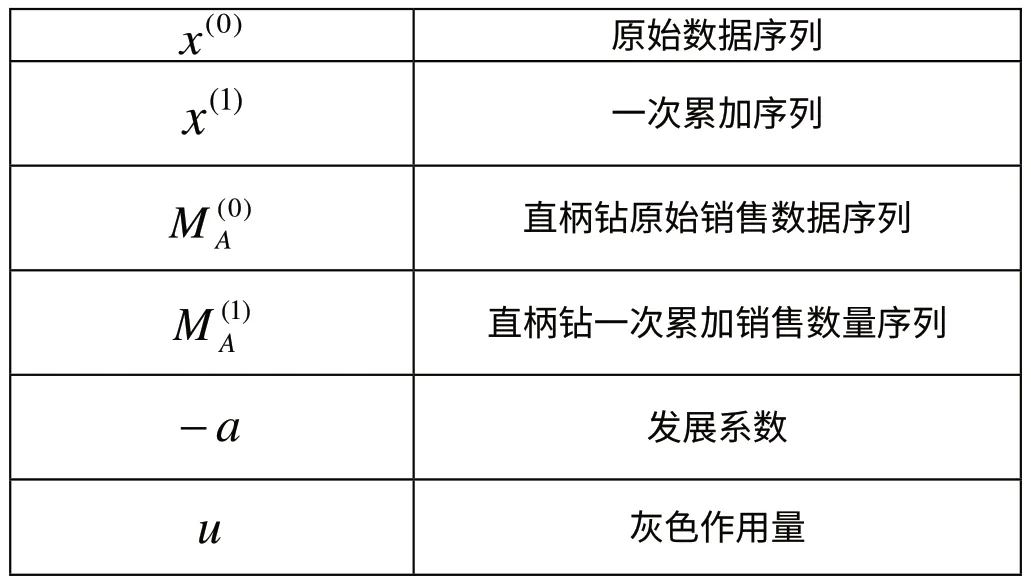
表1 符號說明

三、模型的建立與求解

（一）GM（1，1）模型建立

為了能夠對產品未來銷售數(shù)量進行預測，根據(jù)灰色系統(tǒng)理論，利用灰色預測中的GM(1，1)模型，進行灰色預測。

我們將建立GM(1，1)模型的步驟描述如下。

第一步：累加生成

對原始數(shù)列中個時刻的數(shù)據(jù)依次累加，從而形成新的序列。

設原始數(shù)列為

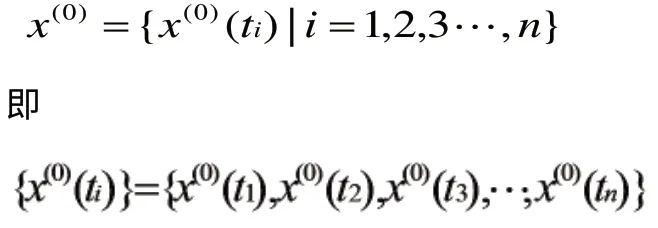
對x(0)做一次累加生成（記作1-AGO)，即令

亦即

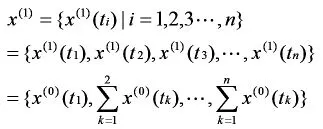
第二步：一次擬合參數(shù)

建立如下GM(1，1)模型即微分方程：

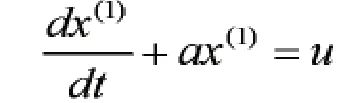
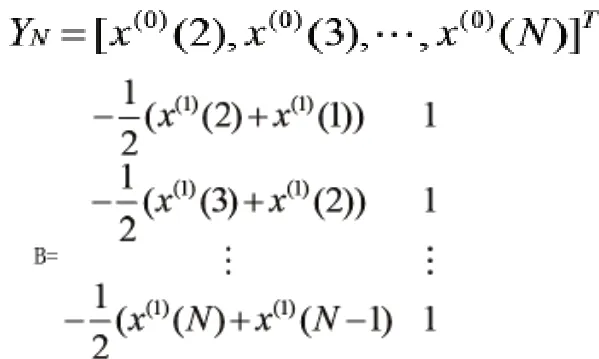
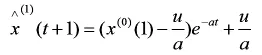
第三步：確定預測值

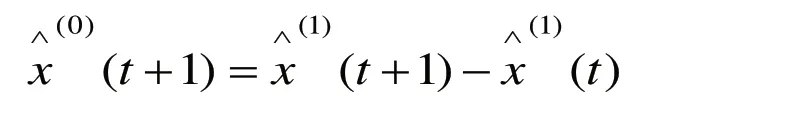
（二）模型的求解

運用以上建立的GM(1，1)模型，結合附錄表1中三種產品的銷售量數(shù)據(jù)，先對直柄鉆（記為A）進行預測。通過MATLAB編程實現(xiàn)（程序見附錄）：

做一次累加生成為

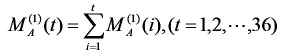
可得(t)的值如表2所示。

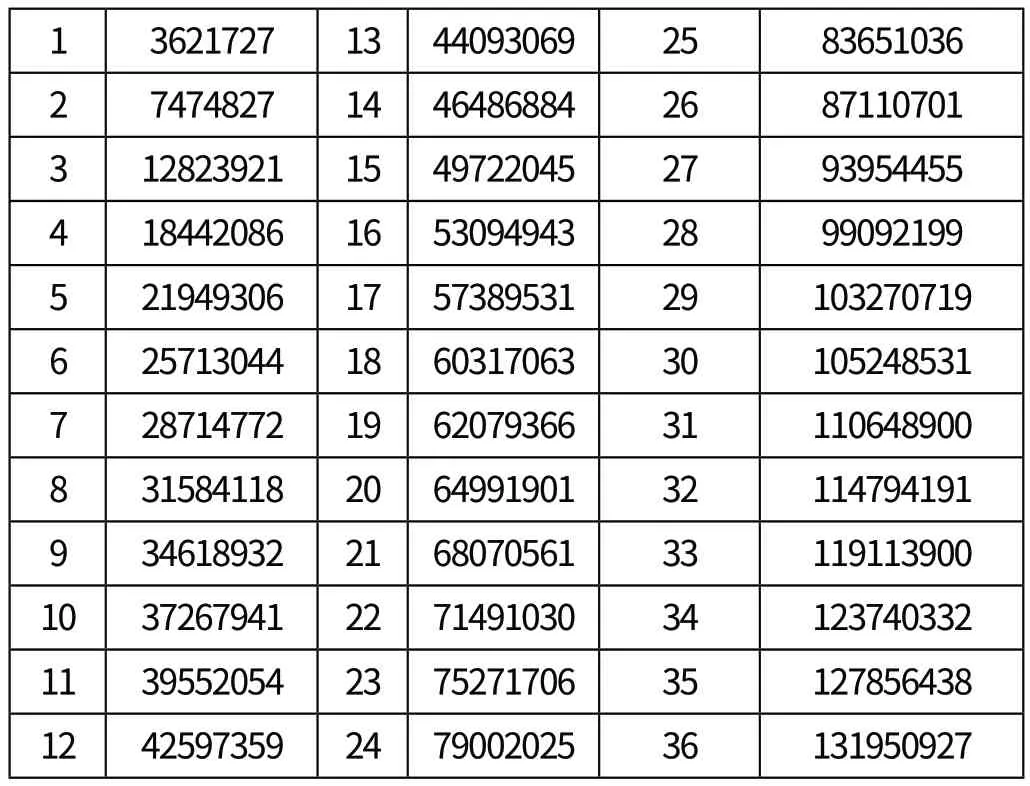
表2 直柄鉆預測值

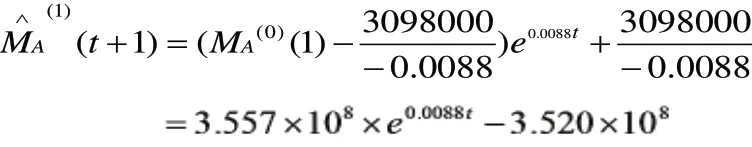
接下來12個月的預測銷售量為（×106)：

對于錐柄鉆、機用絲錐這兩種產品，我們同樣用GM(1，1)模型求得各自的預測值，如表3所示。

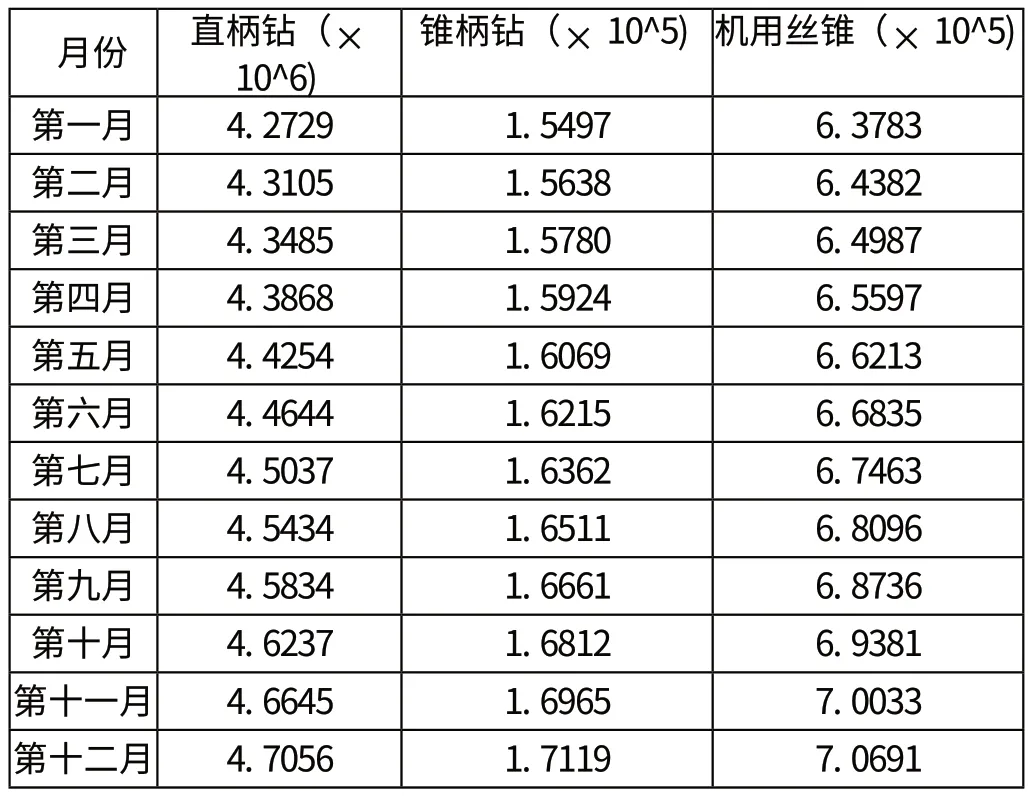
表3 三種產品的預測值

（三）模型分析小結

在許多情況下，GM(1，1)模型可以通過對時間序列長度的不同取舍得到不同的預測結果，但在數(shù)據(jù)變化大或系統(tǒng)明顯受人為控制或外部干擾時，套用GM（1，1）模型進行長期預測所得到的預測值誤差過大。為了盡量減小未來的一些擾動因素對系統(tǒng)的影響，使預測值更具有實際意義，精度更高，我們建立了模型二。

（四）等維灰度預測模型二的建立

對于一個系統(tǒng)來說，隨著時間的推移，未來的一些擾動因素將不斷進入系統(tǒng)，從而對系統(tǒng)增加影響，因此GM(1，1)模型雖可以進行長期預測，但真正有實際意義且精度較高的預測值僅僅是最近的一兩個數(shù)據(jù)，其他更遠的數(shù)據(jù)僅反映一種趨勢。由此可見，沒有必要用一個模型去預測未來的所有值。鑒于這種情況，可先用已知數(shù)列建立GM(1，1)模型的一個預測值，然后把這個預測值補充到已知序列中，同時去掉一個最老的數(shù)據(jù)。這樣，用預測灰數(shù)新陳代謝，逐個預測，依次遞補，直到完成預測目標為止。利用這種方法，即可建立等維灰度預測模型。

（五）模型二的求解

運用以上建立的等維灰度遞補預測模型，結合模型一中得出的之后第一個月的預測值，我們先對直柄鉆進行等維灰度遞補預測。先對直柄鉆銷售數(shù)據(jù)進行等維灰度遞補處理，即將我們計算出的之后第一個月的預測值補充到已知數(shù)列中，同時去掉已知數(shù)列中第一個數(shù)據(jù)，可得一組與已知數(shù)據(jù)等維的新數(shù)據(jù)。這組新數(shù)據(jù)為

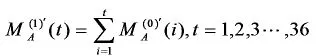
通過MATLAB程序（見附錄）可得：

的值如表4所示。

表4 利用等維灰色預測模型得到直柄鉆預測值

擬合參數(shù)中的B，YN：

B=[-653 -1201 -1657 -2021 -2359 -2653-2948 -3232 -3479 -3745 -3972 -4167 -4448-4779 -5162 -5523 -5758 -5991 -6291 -6616-6976 -7352 -7770 -8176 -8691 -9290 -9756-10064 -10433 -10910 -11333 -11781 -12218 -12628-13047]T

YN=[5349094 5618165 3507220 3763738 3001728 2869346 3034814 2649009 2284113 3045305 1495710 2393815 3235161 3372898 4294588 2927532 1762303 2912535 3078660 3420469 3780676 3730319 4649011 3459665 6843754 5137744 4178520 1977812 5400369 4145291 4319709 4626432 4116106 4094489 4272900]T

將a，u值代入響應函數(shù)，得到的響應函數(shù)為：

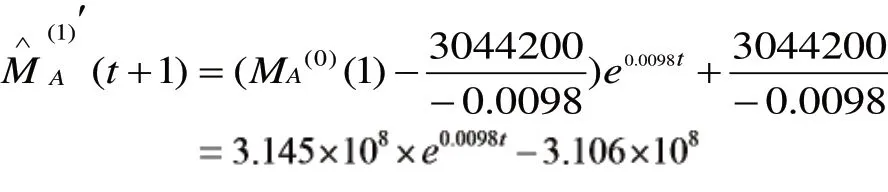
根據(jù)MATLAB程序同時可得接下來的12個月直柄鉆的預測銷售數(shù)量為(×106)：

利用此模型，依次對直柄鉆、錐柄鉆、機用絲錐這三種產品進行等維灰度遞補，對之后12個月的銷售量進行預測，得到預測表如表5所示。

四、模型的評價

我們運用了先進的灰色方法對未來的十二個月三種產品的銷售數(shù)量做了較好的預測。

（一）模型的優(yōu)點

利用灰色方法建模的精度較高，可保持原系統(tǒng)的特征，能較好地反映系統(tǒng)的實際情況。

模型利用題中的數(shù)據(jù)，利用灰色方法進行了大量細致的計算工作，使模型的預測精度大大提高。

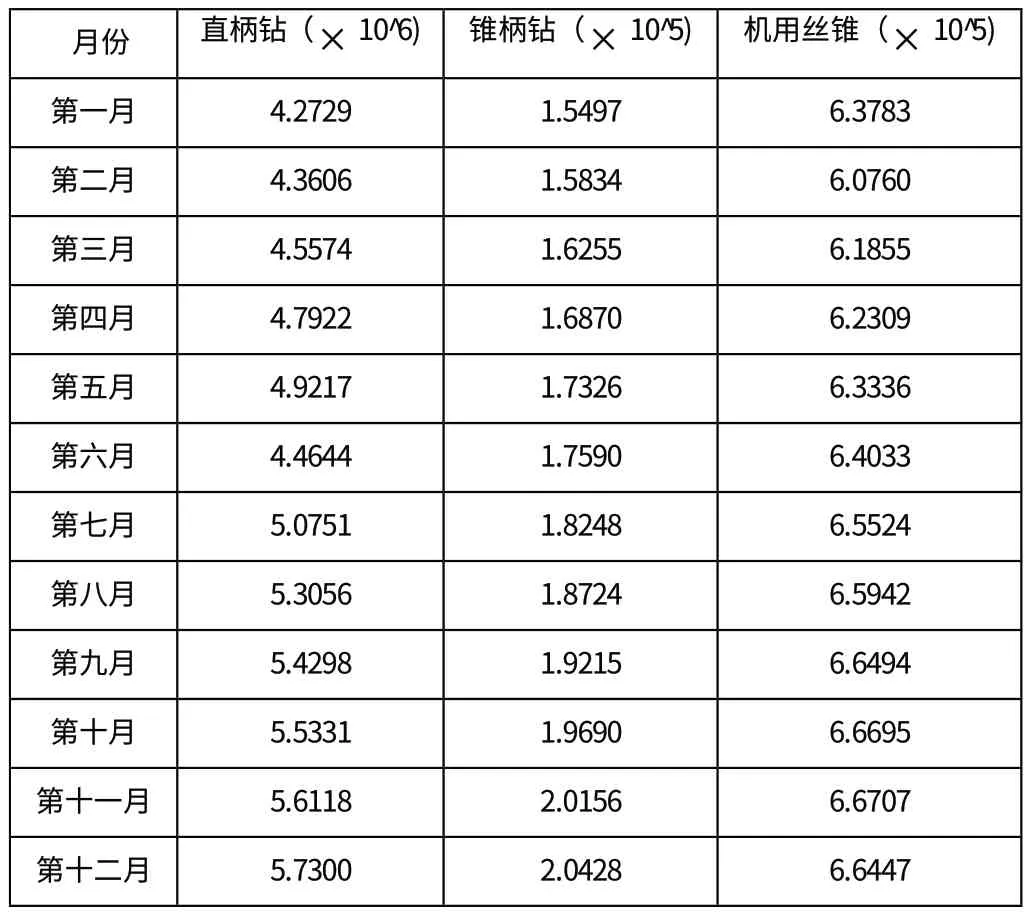
表5 利用等維灰色預測模型得到三種產品預測值

（二）模型的缺點

利用灰色方法運算，過程較復雜，可操作性不強。

[1]黨耀國.灰色預測與決策模型研究[M].北京：科學出版，2009.

[2]錢小軍.數(shù)量方法[M].北京：高等教育出版社，1998.

[3]袁蔭棠.概率論與數(shù)理統(tǒng)計[M].北京：中國人民大學出版社，1989.

[4]楊啟帆，方道元.數(shù)學建模[M].浙江：浙江大學出版社，1999.

[5]壽紀麟.數(shù)學建模—方法與范例[M].西安：西安交通大學出版社，1993.