前向散射和衍射對氣溶膠消光特性測量的影響

袁忠才，林志丹，趙大鵬

(脈沖功率激光技術國家重點實驗室，安徽省紅外與低溫等離子體重點實驗室，電子工程學院，安徽合肥230037)

1 引言

在現代戰爭中，紅外成像觀瞄和制導技術被武器系統廣泛地采用，作為與之相應的對抗技術，紅外遮蔽氣溶膠得到了迅速發展［1－2］。為了設計出性能優越的紅外遮蔽劑，需要對遮蔽材料、遮蔽劑顆粒的粒度等進行優化，其核心就是希望氣溶膠具有較大的消光效率。

通常，對氣溶膠的優化設計都是基于Lamber-Beer定律，即在考慮了氣溶膠顆粒對輻射能的散射和吸收基礎上，利用測量得到的透射衰減值來推導氣溶膠的消光效率［3－5］。在實際測量過程中，通常采用紅外熱像儀來測量輻射的透射衰減［6］，氣溶膠顆粒對輻射的前向散射和衍射將到達熱像儀的聚光鏡頭，加入透射光，從而對透射衰減值帶來影響。由于前向散射和衍射通常會形成前向峰值［7－8］，因此其影響不可忽略。本文基于Mie's散射理論，引入束效率因子和有效消光效率因子，分析了前向散射和衍射對透射測量帶來的影響，進一步得出了消光截面積測量的誤差;在此基礎上，提出了減小該影響所帶來誤差的方法。

2 前向散射和衍射的影響

考慮一個厚度L的氣溶膠層，一輻射束照射并穿透之(如圖1所示)，然后經透鏡會聚后到達探測器，根據朗伯－比爾定理可知透射的輻射強度。

圖1 氣溶膠中光波透射率測量原理圖Fig．1 schematic of testing the optical transmissivity of the aerosol

其中，I0是入射輻射強度;β(λ)為消光系數，當粒子尺度不均勻時，有:

其中，n(r)是粒子半徑r的分布函數;N為氣溶膠粒子數密度;σe(λ，r)是指半徑為r的粒子在波長為λ處的消光截面，可以利用Mie散射理論求出。利用平均消光截面可得到:

其中，ρ為氣溶膠粒子數密度;σ為粒子的平均消光截面，可利用氣溶膠產生前后探測器所記錄的輻射強度值得到:

由于氣溶膠顆粒對入射輻射的前向散射和衍射會形成朝向探測器方向的前向峰值，到達探測器的這一部分輻射將被記錄為非散射光，使得存在煙幕時測得的輻射強度It增大，從而將使利用式(4)計算得出的平均消光截面積減小。

考慮單位幅度的時諧入射場，球形粒子在球坐標系中的散射遠場可表示為:

其中，Esθ為處于由入射和散射方向構成的散射平面內的散射遠場分量;Es為正交分量;θ為散射角;為入射電場方向與散射平面的夾角。散射函數S1和S2分別為:

其中，Mie系數an，bn取決于粒子內核和包覆層的特性，可以利用 Volkov［9－10］等人提供的方法得到，而πn，τn僅與角度有關，可以利用Legender多項式求得［7－8］，這里不再贅敘。

散射函數S1和S2中包含了顆粒的衍射貢獻。對于半徑為a的顆粒，其衍射函數為:

其中，x=ka為粒子的尺寸因子;k為波數。則不計衍射的散射場為:

圖2分別給出了尺寸因子x=5，折射率為m=0．603+6．37 i的黃銅顆粒在扣除和不扣除衍射條件下的散射函數，其中上半部分為S1，下半部分為S2。圖中均將最小值歸一化到0 dB。對比左右兩列圖可以看出，在前向上有較強的衍射峰，且衍射峰對應的角度約為θmax=180°/x;尺寸因子越大，前向散射和衍射效應均更顯著。

圖2 上下半園有無衍射峰值時的角散射圖(dB)Fig．2 angular scattering diagram in logarithmic(dB)scale without(left)and with(right)diffraction peak for spheres of different size parameters，S1upper，S2lower semicircle

為了估算前向散射和衍射的貢獻，引入束效率因子ηb，表示在一定角度范圍內的散射光在總散射光中所占的比例:

其中，積分上限θlim由探測器對粒子的張角決定。根據定義，式(9)應滿足歸一化要求，即當θlim=π時，要求有ηb=1。同時，可得到衍射信號的束效率因子:

圖3給出了由式(9)和式(10)得到的對應不同尺寸因子的束效率因子，其中粒子的折射率為m=0．603+6．37 i。從圖3可以看出，衍射信號對應的束效率因子(圖中點線所示)類似一個階梯函數，表明在衍射主要集中在前向范圍內;而粒子的漫散射分布相對較均勻;兩者的綜合作用使得總的散射束效率因子(圖中實線所示)在一定角度后變化趨緩。同時，在前向小角度范圍內，衍射對探測器所測得輻射的貢獻大于前向散射;對于大粒子兩種效應更顯著。

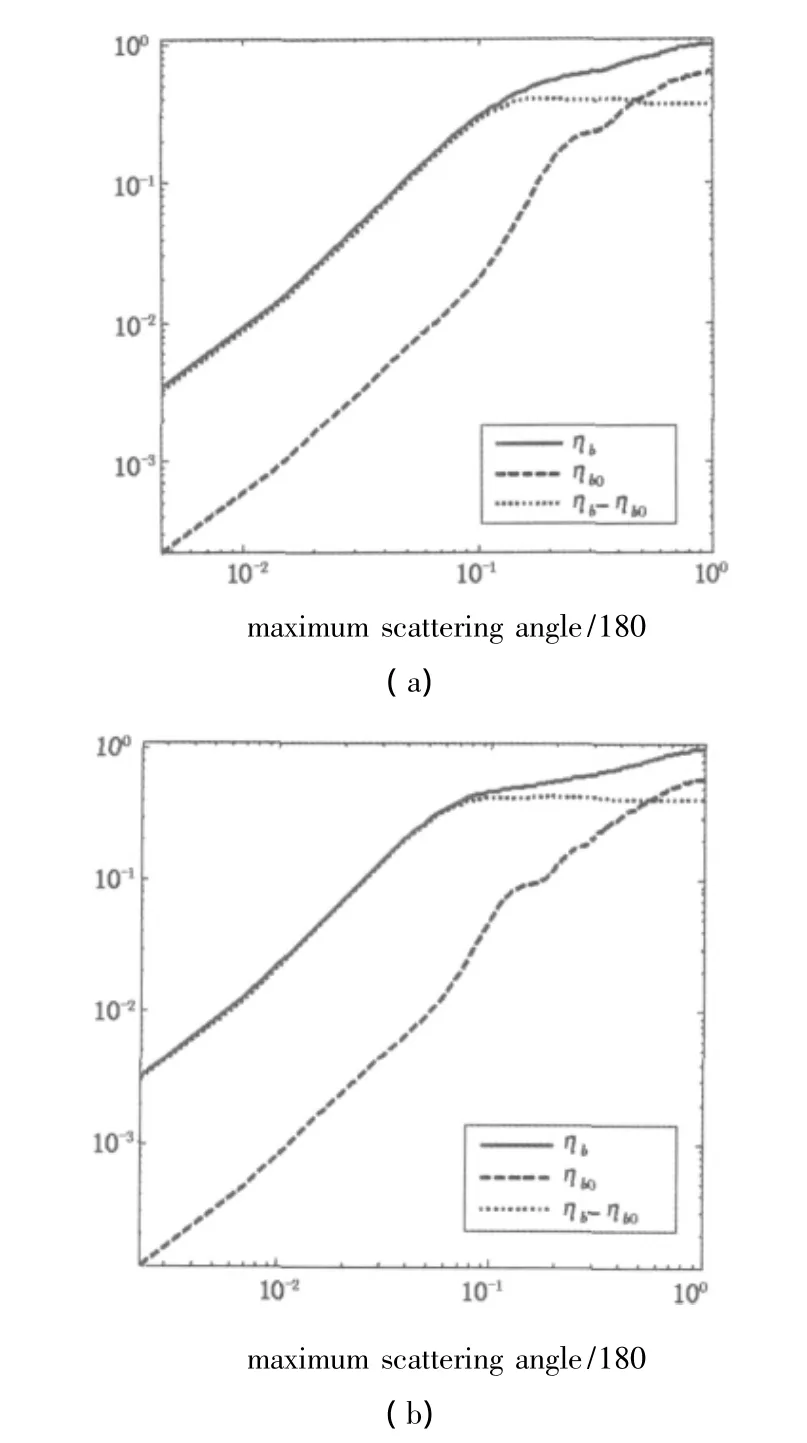
圖3 一定折射率下介質球光束效率與θlim的關系Fig．3 beam efficienciesηb(solid line)and ηb0(dashed)and their difference(dotted)of a dielectric sphere versus θlimfor refractive indexm=0．603+6．37i，size parameter:1:x=5，2:x=10

3 消光截面計算的誤差分析

在氣溶膠特性的透射測量中，氣溶膠粒子通常遠離探測器。假設粒子到探測器聚光孔(如熱像儀的光學鏡頭)的距離為L，熱像儀光學鏡頭的半徑為d，則在一定角度范圍內被粒子散射的輻射將達到光學鏡頭，被最終被探測器接收，如圖4所示。

圖4 氣溶膠粒子對探測器的光學散射示意圖Fig．4 schematic of light scattering from aerosol particle to detector

對于特定的探測器，假設其聚光孔(探測器的聚光透鏡)大小為d=2 cm，則散射接收角φ隨氣溶膠粒子與探測間距離的變化如圖5所示。當距離和散射接收角已知時，可以利用圖3得到對應粒子的散射束效率因子。同時，為了考察前向散射和衍射對粒子消光特性的影響，引入有效散射和消光截面，分別為:

其中，σs和σe=σa+σs為通過透射衰減測量得到的散射截面和消光截面，而粒子的吸收截面不受前向散射和衍射的影響。

圖5 散射接收角與粒子至探測器距離的關系Fig．5 scatter-receiving angle vs．particle-detector distance

表1 光束效率和有效消光截面比的典型數值Tab．1 typical values of the beam efficiency and the ratio of the effective extinction cross section to experimental one

表1列出了對應幾種尺寸因子x和距離L的束效率因子以及有效消光截面與實驗測量值的比值。可以看出，在扣除了前向散射和衍射對透射測量的影響后，得到的有效消光截面將大于原本的實驗測量值。對于尺寸因子一定的粒子，粒子與探測器間的距離越小，兩種消光截面間的差距越大。因此，為了減小由前向散射和衍射導致的消光截面測量誤差，應該使得探測器到氣溶膠煙幕的距離盡可能的遠，尤其是對于顆粒較大煙幕的測量。對于吸收占主導的煙幕，雖然前向散射對消光截面的影響較小，但衍射的影響仍然存在，因此探測器到氣溶膠煙幕的距離也應盡可能的遠。考慮到紅外煙幕的最佳粒徑與所遮蔽輻射的波長相當［7－8］，常用煙幕通常采用粒徑處于最佳粒徑附近的顆粒，這時對應的尺寸因子處于10以下，因此對于紅外煙幕測試，應保證探測器到氣溶膠煙幕的距離在100 m以上。

4 結論

基于Mie's理論，我們分析了透射衰減和消光截面測量中前向散射和衍射影響，表明兩種影響不可忽略，為了減小這一影響帶來的誤差，在測量時應保證探測和氣溶膠之間的距離盡可能的遠。這對于氣溶膠光學特性的測量與分析具有現實的指導意義。

［1］ Ladouceur H D．Obscurants for infrared countermeasure［R］．NRL/FR/6111－97－9878．

［2］ Harris B L，Shanty F，Wiseman W J．Chemical in war．In kirk-othemer encyclopedia of chemical technology［M］．New York:Wiley-interscience，1979，5(3):405 －408．

［3］ Jiachun Wang，Jiaming Shi，Jiayin Wang，et al．Infrared extinction coefficients of artificial aerosol［J］．Defence Science Journal，2007，57(4):417 －424．

［4］ LiMing，Fan Dongqi，Yin Chunyong．Study on corresponding relation of laser and infrared transmittivity for some smoke screen ［J］．J．Infrared Millim．Waves，2006，25(2):127 －130．(in Chinese)

李明，范東啟，殷純永．煙幕激光和紅外透過率對應關系研究［J］．紅外與毫米波學報，2006，25(2):127－130．

［5］ Li Xuebin，Li Chao，Xu Qingshan，et al．The study of obtaining multi-wavelength aerosol optical characteristics［J］．Laser ＆ Infrared，2008，38(3):252 －254．(in Chinese)

李學彬，李超，徐青山，等．獲取多波長氣溶膠光學特性的方法研究［J］．激光與紅外，2008，38(3):252－254．

［6］ Xu Bo，Shi Jiaming，Wang Jiachun，et al．Measurement of infrared transmissivity of smoke using a thermal imager［J］．Defence Science Journal，November，2006，56(5):785－790．

［7］ H C van de Hulst．Light scattering by small particles［M］．New York:Wiley，1957．

［8］ C F Bohren，D R Huffman．Absorption and scattering of light by small particles［M］．New York:Wiley，1983．

［9］ Volkov N G，Kovach V Yu．Scattering of light by inhomogeneous spherically symmetrical aerosol particles［J］．Izvestiya Atmospheric and Oceanic Physics，1990，26(5):381－385．

［10］ Perelman A Y．Scattering by particles with radially variable refractive indices［J］．Applied Optics，1996，35(27):5452－5460．