基于多目標規劃的最優再保險策略

李秀芳，景 珮

(南開大學經濟學院，天津300071)

直接保險人是經營風險的個體，風險聚合和風險分散是經營的核心所在。直接保險人在承保某類風險業務時，由于資本的限制和償付能力要求，通常會將一部分業務轉給再保險人。因此，再保險是一種十分常用且重要的風險轉移手段:一方面，保險人分出業務過多會顯著地降低利潤水平;另一方面，分出業務過少、承擔的風險過高可能導致償付能力不足甚至引發破產。因此，判斷合理的自留業務量，即最優再保險決策是十分重要并有意義的。

若要研究最優再保險決策，首先要判斷何為“最優”，即“最優”的標準是什么。出于再保險決策的重要性，目前已有大量成熟的研究關注這一方面。如Manuel Guerra等［1］以盈余的期望效用準則和破產概率準則分別探討了再保決策的最優自留額;Jun Cai等［2，3］以直接保險人再保后的剩余風險(VaR和CTE)作為衡量標準;周明等［4］將風險調整資本收益率引入再保決策，判斷最優的再保比例。由此可見，盡管不同的研究成果選擇的指標和判斷準則不同，但大體上都反映了收益目標或是風險目標。然而，這些研究都是選擇的單一目標，事實上，保險人處在復雜的經濟環境中，同時追求收益最大和風險最小，不能忽視其中任一目標。對于再保險決策，保險人的目標首先是降低風險，但與此同時也不能因追求風險最小就放棄了利潤目標。單一目標研究無法全面評判保險人面臨的權衡取舍，這一問題在多目標最優化問題中得到了很好的解決。

多目標最優化問題最早由意大利經濟學家Pareto在1896年提出，它是指系統方案的選擇取決于多個目標的滿足程度。多目標優化和單目標優化的重要區別在于單目標優化通常只有一個最優解，而多目標優化中，由于是對多個目標同時優化，目標間往往相互沖突，因此最優解集通常是一個集合，這個解集被稱為Pareto最優解或非劣解。解決一個多目標優化問題通常包括兩個方面，即搜索和決策①。一些傳統的多目標問題的解法是在優化過程中加入研究者(決策者)的偏好信息，求得折中方案，并在此基礎上進一步搜索，即在搜索前決策或邊搜索邊決策。這樣的求解過程類似黑匣子，其他人無法看到不同的偏好信息對結果的影響。另一種求解方法是在沒有任何喜好信息的情況下優化，給出Pareto最優解集，最后由決策者做出選擇［5］。本文的研究采用的是第二種方法，即給出優化問題的Pareto最優解集。

一、模型建立

假設保險人承保了某類業務風險總額為X，X為非負的連續隨機變量，具有分布函數F，并且均值和方差有限。假設保險人自留的風險總額為I(X)，保險人收取了總保費P，自留保費PI，分出給再保險人的保費則為 P －PI，應有

影響直保公司再保策略的因素主要包括:收益目標、風險考慮和資本約束。首先是收益目標，直接保險人是經營風險的個體，無論經營中進行何種決策，利潤目標都是首先要關注的。在這里，采用風險調整資本收益率(RORAC)作為衡量利潤率的指標，采用這一指標的重要原因是保險人在決策時不僅關注期望利潤的絕對值大小，更關注投入的每一單位資本所能得到的期望資本回報率，資本收益率可以完美的表達這一概念。風險調整資本收益率的計算公式［6］為風險調整資本收益率=期望利潤/風險調整資本，其中風險調整資本應為保險人在實際經營業務中為該項業務安排的實際資本，這樣計算得到的RORAC充分表達了公司投入的每單位資本得到的期望利潤。令 TI(X)=I(X)－PI(X)，表示自留保費不足以彌補自留風險總額的部分，根據巴塞爾協議Ⅱ，風險調整資本采用在險價值(VaR)的方法計算，即在一定置信水平α下損失的最大可能的分位數。風險調整資本U1可以表示為

因此，風險調整資本收益率可以表示為

在考慮了收益目標后，還要考慮風險目標。直接保險人在進行再保險時將業務、保費、利潤的一部分轉讓給再保險人，主要的目的是控制風險。盡管直接保險人在承保業務時收取了充分且合理的保費，并且按照一定概率下最大可能損失的估計安排了相應的資本，但是保險人仍然可能出現償付能力不足的情況，即資本加上保費仍然不足以彌補損失賠付的情況。因此，在考慮再保決策時，應該最小化償付能力不足的風險，采用償付能力不足的條件期望損失作為衡量標準［7］。償付能力不足的條件期望損失衡量了當保險人按風險調整資本U1安排資本時，若資本仍不足以彌補損失賠付與保費之間差額TI(x)，這部分差值的平均水平，可以表示為

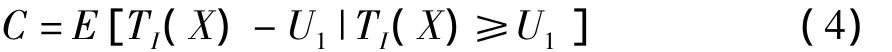
除了收益目標、風險目標，直保公司還需考慮資本約束。當直接保險人的資本充足，即資本水平足以支撐現有業務時，可以利用之前設定的收益、風險目標函數選擇最優的自留比例。但是當資本不充裕時，直接保險人出于公司內部風險管理及監管機構的償付能力監管要求必須分出一定比例的業務。事實上，我們認為直接保險人的資本可以分為3個層次［8］:一是公司的實際資本，即對于該項業務現有可用的資本總額U0;二是公司出于內部風險管理，針對業務計算得到的要求資本總額，可以用前文提出的風險調整資本U1表示;三是監管機構針對償付能力監管為保險人提出的最低資本要求U2。因為公司內部的要求資本和法定最低資本都與自留業務比例相關，因此可以建立自留業務比例需滿足的資本約束不等式:max{U1，U2}≤U0。它表示直接保險人允許的自留業務額受當前的資本水平制約。事實上，公司出于風險管理計算得到的要求資本U1通常會大于法定最低資本要求U2，因此，上式可以轉化為

綜上所述，可以建立最優再保險策略的模型為

二、最優再保險策略

理論上存在多種多樣的再保險形式，只要滿足式(1)就可成為一種再保險策略。但是在保險實務中，再保險主要包括比例再保險和非比例再保險。成數再保險是比例再保險中常用的形式，它是指直接保險人選擇一個自留比例，并按此比例在保險人和再保險人之間分配業務。而在非比例再保險中，停止損失再保險十分常見，它是以原保險人一段時間的總損失金額為基礎，原保險人選擇一定數額的自留業務，并將超過此額度的損失轉嫁給再保險人。

1．最優成數再保險策略

假設直接保險人承保了風險總額為X的業務，自留比例為a，有I(X)=aX，因此分出給再保險人的風險總額為(1－a)X。直接保險人共收取保費P，再保險人收取的再保險費采用期望準則②，PR=(1+η)E(1－a)X，則直接保險人的自留保費為P－PR。此外，對于成數再保險，有U1=a VaRX(α)+PR－P。

推論1:當資本U0＜VaRX(α)－P時，最優自留比例的上限隨資本的增加而提高，當U0≥VaRX(α)－P時，最優自留比例的上限為1(見圖1)。

圖1 自留比例最優解集的上限隨資本變化

2．最優停止損失再保險策略

當直接保險人采用停止損失再保險時，假設自留額為b，當風險總額小于b時保險人自留全部風險，當風險總額大于b時，保險人自留額度為b的風險，即I(X)=XΛb。因此分給再保險人的風險總額為(X－b)+，并假設再保險人收取的再保險費為PR=(1+η)E(X－b)+。

引理1:當b＜VaRX(α)時，風險調整資本收益率(RORAC)先增加后減小，并且存在一點b1使RORAC達到極大值;當b≥VaRX(α)時，RORAC隨著自留額b的增加而增加。

引理2:當b＜VaRX(α)時，償付能力不足的條件期望損失(C)先減少后增加，并且存在一點b2，b2=，使C達到極小值;當b≥VaRX(α)時，C隨著自留額b的增加而增加。可以證明b1≥b2。

定理2:根據U1的定義有U1(b)≡VaRX(α)Λb+(1+η)δ(b)－P，

若

若

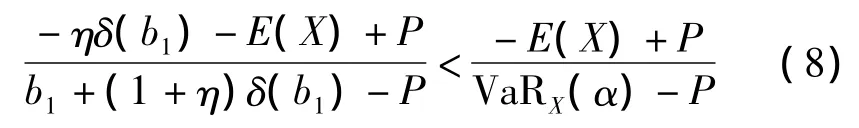
當 U0＞U1(S－1X(α))時，M1問題的 Pareto最優解集為 b∈［b2，b1］∪［b3，∞ )，b3滿足 RORAC|b=b1=RORAC|b=b3;當 U0＜U1［S－1X(α)］時，M1問題的 Pareto最優解集為 b∈{b1，min［b1，g1］}∪{min［b3，g2］，∞}，g2滿足 VaRX(α)+(1+η)δ(g2)－P=U0。

由引理1可知，風險調整資本收益率函數存在兩個極大值點，b=b1，b=+∞，當式(7)滿足時有RORACb=b1＞ RORACb－＞+∞，函數的最大值在 b1處取得。此時問題的最優解集取決于初始資本水平，若資本水平充裕，對自留額的選擇沒有限制，則最優自留額應在b1和b2之間的范圍選擇;若資本不夠充裕，自留額的選擇范圍變小，具體取決于資本水平。

當式(8)滿足時，風險調整資本收益率函數的最大值在正無窮處取得，此時M1問題的最優解集由兩部分組成:第一部分與前面的情況相同;第二部分是風險調整資本收益率大于b1處的值之后的部分。這表示直接保險人為追求更高的收益率而選擇更大的自留額，同時承受更大的償付能力不足風險。從上面的定理可以看出，根據保險人現有資本的不同水平，最優停止損失再保險策略也有所不同。當保險市場對保險資本的監管比較松時，保險人可以適當的為追求高收益率而選擇較高的自留額度。但無論如何，更高的風險調整資本收益率總意味著更大的償付能力不足風險。

推論2:若式(7)滿足，當 U0＜U1(b1)時，Pareto最優解集上限隨資本水平的增加而增加，當U0≥U1(b1)時，最優解集的上限保持不變。

推論3:若式(8)滿足，Pareto最優解集由兩部分組成，第一部分上限與推論1中結論相同，第二部分下限在U0＜U1(b3)時隨資本的減少而降低，在 U0≥U1(b3)時保持不變。

由圖2可見，資本水平越低，Pareto最優解集的上限越低，下限越高，因此再保險自留額水平可選擇的范圍越小，最優自留額受到資本的約束越強。當資本大于一定水平時，最優自留額的選擇不受資本限制。

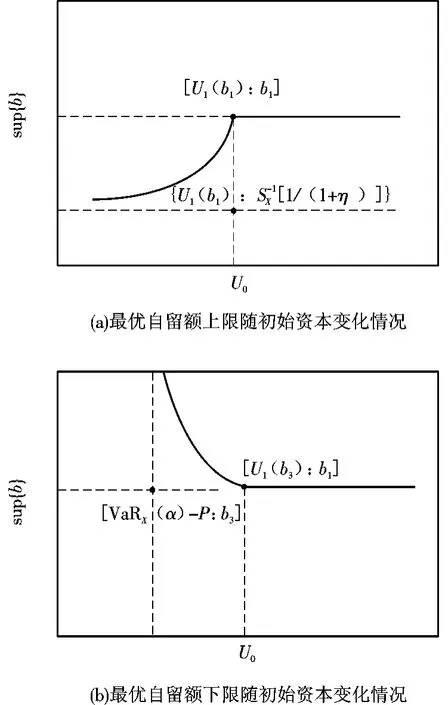
圖2 Pareto最優解集的邊界隨資本水平變化情況

三、算例分析

假設一家財產保險公司承保的火險風險總額X服從帕累托分布，F(X)=并有 θ=1 000 000，β=8。于是該公司未來一年內的火險期望賠付為14.286萬元。如果選擇置信度 α=0.1，有VaRX(α)=33.35萬元。假定直接保險人和再保險人制定保費時的邊際ξ=5%，η=7%。

首先，假設保險人采用成數再保險策略，根據定理1，最優自留比例與初始資本水平有關，若初始資本U0=5萬元，有最優自留比例α須滿足0≤a≤0.261;當初始資本U0=10萬元時，有0≤a≤0.538。可以看出，最優自留比例的上限隨初始資本的增加而提高，初始資本越充裕，最優自留比例上限越大，直接保險人受到的限制越小。當初始資本大至一定程度時，直接保險人的再保自留比例可以不受資本限制，根據自己的偏好自由選擇自留比例。

其次，保險人采用停止損失再保險策略，在這一例子中可以驗證定理2中的式(7)滿足。因此，問題的最優解集為:若初始資本U0≤20.39萬元，最優自留額應在0.85萬元到9.43萬元的范圍內選擇;若U0≤20.39萬元，最優自留額的選擇可能受初始資本水平約束，是否存在制約受 b1，g1的大小關系影響。當U0=10萬元時，最優自留額度的范圍不變，而當U0=2萬元時最優自留額應在0.85萬元至8.19萬元之間。事實上，最優自留額度上限與初始資本關系的散點圖見圖3。

圖3 最優自留額上限與初始資本的關系

可以看到，當U0小于2.59萬元時，最優自留額度上限隨初始資本的減少而降低，當初始資本為零時，自留額度上限達到最小0.29萬元。當U0大于2.59萬元時，初始資本對最優自留額度不存在約束，自留額度的選擇只由目標函數風險調整資本收益率和償付能力不足風險決定。

假定初始資本大于2.59萬元，可以得到風險調整資本收益率與自留額度的關系(見圖4)。

從圖4可以看出，當自留額度小于9.43萬元時，RORAC不斷增加，并且在b=b1=94 258處取得最大收益率7.1%;當自留額度大于9.43萬元小于33.35萬元時，RORAC逐漸減少，并在b=333 521處取得局部極小值2.85%;當自留額度大于33.35萬元時，RORAC再次逐漸增加。

償付能力不足的尾部損失與自留額度的函數曲線見圖5。

圖5的橫坐標范圍為［0，20 000］，可以看出當自留額度小于0.85萬元時，尾部損失C不斷減少，并在b=b2=8 493處取得最小值13.73萬元;當自留額度大于0.85萬元時，尾部損失C逐漸增大。因此，該停止損失再保險的最優自留額度范圍應在0.85萬元到9.43萬元之間，隨著自留額的增加風險調整資本收益率不斷增加，償付能力不足尾部損失也不斷增大。只要直接保險人在這一范圍選擇自留額度就是有效率的，不會出現收益率低但相對風險高的情況;同時所有有效率的收益－風險組合都包含在這一范圍中。

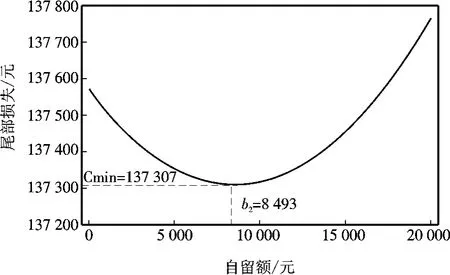
圖5 償付能力不足尾部損失與最優自留額度的關系

四、結 語

本文由收益目標、償付能力風險目標和資本約束三個方面出發，建立了比例再保險和停止損失再保險的最優策略模型，分別得到問題的Pareto最優解集，探討了初始資本水平對再保險策略的影響并進行數值分析，得到的結論包括當自留業務水平滿足最優解集范圍時，風險調整資本收益率隨自留水平的增加而增加，償付能力不足風險也隨自留水平的增加而增大，風險調整資本收益率與償付能力不足風險之間呈正向變化的關系。當初始資本充裕時，資本對自留業務水平不產生影響，當初始資本不充裕時，自留額度選擇受初始資本水平約束，資本越少，自留額度可選擇的范圍越小。

注釋:

①搜索是指在優化過程中，可行解集被求解出來;決策是強調從可行解集中選擇合適的解。

②在保險理論中，保費的制定通常有一般期望準則、標準差準則、方差準則等。

［1］Manuel Guerra，Maria de Lourdes Centeno．Optimal reinsurance policy:The adjustment coefficient and the expected utility criteria［J］．Insurance:Mathematics and Economics，2008，42(2):529-539．

［2］Jun Cai，Ken Seng Tan．Optimal retention for a stop-loss reinsurance under the VaRand CTErisk measures［J］．ASTIN Bulletin International Actuarial Association-Brussels，Belgium，2007，37(1):93-112．

［3］Jun Cai，Ken Seng Tan，Chengguo Weng，et al．Optimal reinsurance under VaR and CTE risk measures［J］．Insurance:Mathematics and Economics，2008，43(1):185-196．

［4］周 明，陳建成，董洪斌．風險調整資本收益率下得最優再保險策略［J］．系統工程理論與實踐，2010，30(11):1931-1937．

［5］鄭金華．多目標進化算法及其應用［M］．北京:科學出版社，2007．

［6］陳學華，韓兆洲，唐 珂．基于VaR和RORAC的保險基金最優投資研究［J］．數量經濟技術經濟研究，2006，23(4):111-117．

［7］Ingo Oesterreicher，Andreas Mitschele，Frank Schlottmann，et al．Comparison of multi-objective evolutionary algorithms in optimizing combinations of reinsurance contracts［C］//GECCO＇06．Proceedings of the 8th annual conference on genetic and evolutionary computation，2006:747-748．

［8］Yuriy Krvavych，Michael Sherris．Enhancing insurer value through reinsurance optimization［J］．Insurance:Mathematics and Economics，2006，38(3):495-517．