時間序列模型在醫院感染發生率擬合預測中的比較研究*
李 紅 潘東峰 郭忠琴 王 嵐 梁沛楓△
隨著現代醫學的快速發展,侵入性診療技術的開展以及放、化療等使醫院感染發生的影響因素復雜化,醫院感染不斷出現新的特點,產生新的危害,其已成為醫學界亟待解決的重大問題。醫院感染的監測能及時發現醫院感染病例及其相關因素,可有效降低其發生率。目前對醫院感染的監測雖已從全面綜合性監測轉向針對性強的目標性監測或靶位監測,但感染控制的監測模式仍處于“形式化”感控階段〔1〕,實現對醫院感染危險因素造成的危害進行事前監測,從而建立醫院感染預警模式則是醫院感染管理工作今后發展的重要方向。利用統計預測分析技術,對醫院感染進行預測性數據挖掘是對醫院感染危險度監測的前瞻性研究方法。本研究選擇寧夏某大型綜合醫院為監測點,嘗試應用三種不同的時間序列模型對醫院感染發生率進行模擬構建,探討模型在醫院感染領域應用的適用性及價值,并應用最優時間序列模型以間接監測醫院感染發展趨勢,以期發現醫院感染的潛在規律,發出早期預警,從而提高監控效率。
資料與方法
1.資料來源
資料來源于寧夏某三甲醫院2005年1月1日至2011年10月31日出院病人數據庫及該院醫院感染監測網。
2.數據整理
將醫院HIS系統中的2005~2010年出院病人數據庫轉換為能滿足統計預測分析所需的數據環境,并篩選符合醫院感染診斷標準的全部病例,對篩查出的醫院感染病例與醫院感染監測網上報的院感病例進行核對,補全數據庫中漏填病例,計算醫院感染發病率。診斷標準及感染率計算方法根據衛生部頒布的《醫院感染診斷標準(試行)》。
3.方法簡介
(1)ARIMA 模型〔2-3〕,即自回歸滑動平均混合模型,主要分析時間序列的隨機性、平穩性和季節性。ARIMA模型中的三個參數p、d、q分別表示自回歸階數、差分階數和移動平均階數,其數學表達式為:
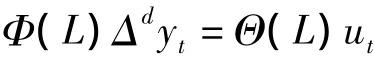
其中Φ(L)和Θ(L)分別表示L的p,q階特征多項式;t表示時間;yt表示時間序列;ut為白噪聲過程。若序列具有線性趨勢或周期性,可通過d階差分或季節差分使序列滿足ARIMA的建模條件,最后通過殘差序列檢驗擬合的模型是否有效,并可通過AIC準則或BIC準則判斷多個模型中的最優模型。
(2)指數平滑法〔2〕的原理是對離預測期較近的觀察值賦予較大的權數,對離預測值較遠的觀察值賦予較小的權數,權數由近到遠按指數規律遞減。其基本形式的數學表達式為:
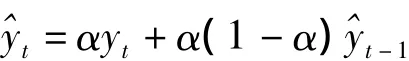
其中,yt是實際值序列,是平滑值序列,是上期平滑值,α是平滑系數,也叫衰減因子,平滑系數的取值范圍為:0≤α≤1。
(3)灰色模型〔4-5〕的理論基礎是一般的非負準光滑序列經過累加生成后,都會減少隨機性,呈現出近似的指數增長規律。原始序列越光滑,生成后指數規律與越明顯。其數學表達式為:
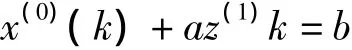
其中,z(1)k=1/2[(x(1)(k)+x(1)(k-1)]GM(1,1)模型中的參數-a為發展系數,b為灰色作用量。-a反映了及的發展態勢。
(4)模型效果的評價
采用相對誤差絕對值平均MAPE(mean absolute percentage error)及其相應的等級評定〔5〕來評價ARI-MA模型、指數平滑模型、灰色模型對醫院感染發生率資料的擬合效果。
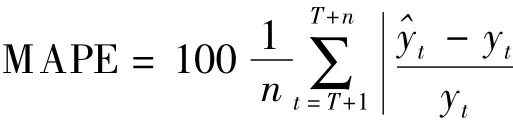
T表示樣本容量,n表示樣本外預測期數,^yt表示預測值,yt是實際值。
4.分析軟件
ARIMA模型和指數平滑模型運用eviews6.0進行擬合,灰色模型應用《灰色系統理論及其應用》〔4〕一書的配套軟件進行建模。
結 果
1.醫院感染時序圖
以醫院感染的月發病率信息為縱軸,對應的時間為橫軸,繪制醫院感染率時序圖(圖1),時序圖顯示各月醫院感染的發病率呈現出一定波動,且每年均出現發病高峰月,醫院感染率具有季節性和周期性。
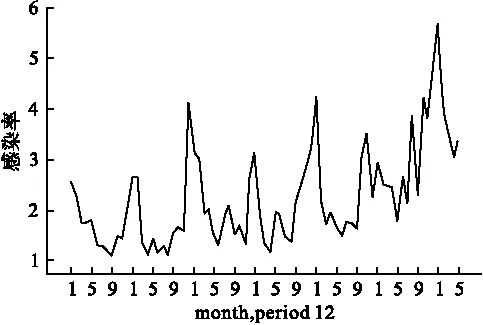
圖1 寧夏某三甲醫院醫院感染率時序圖
2.ARIMA 模型
對醫院感染率序列進行季節調整后的單位根檢驗再次確定了醫院感染的季節性,對原變量進行一階差分、季節差分后,嘗試擬合不同的ARIMA季節模型,依據信息量準則判別模型的優劣,其中AIC和SBC最低的模型是最好的模型。最終確定模型為ARIMA(0,1,1)(0,1,1)12,其 AIC 和 BIC 值分別為 1.9047、1.9752。通過殘差自相關函數圖檢驗模型的隨機誤差項是一個白噪聲序列。故 ARIMA(0,1,1)(0,1,1)12模型是所要確定的最終模型,其對應的模型表達式為:

醫院感染序列實際值與預測值的MAPE值為12.50,對應的擬合圖形如圖2。
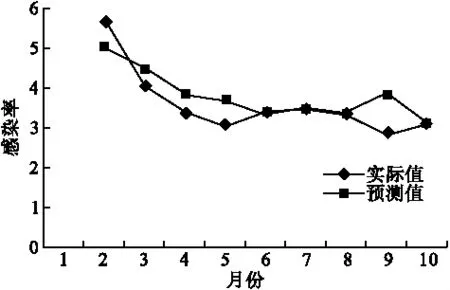
圖2 感染率實際值與ARIMA模型預測值趨勢圖
3.指數平滑模型
對原序列擬合加法性季節Holt-Winters法和乘法性季節Holt-Winters方法,其殘差平方和分別為19.34和19.38,以殘差平方和最小為最合適模型,并進行殘差圖檢驗,最終加法性季節Holt-Winters法是指數平滑法中最合適模型。其對應的模型表達式為:
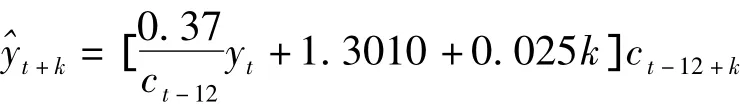
醫院感染序列實際值與預測值的MAPE值為10.41,對應的擬合圖形如圖3。
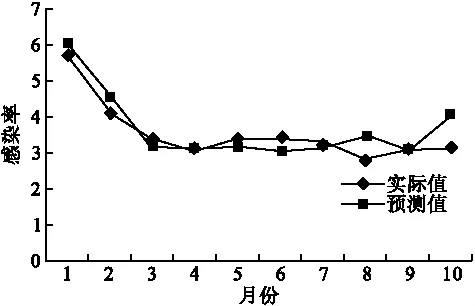
圖3 醫院感染率實際值與指數平滑法預測值趨勢圖
4.灰色模型
對原序列進行灰色模型的可行性判斷,結果顯示,σ(k)∈(0.5000,2.6242),級比檢驗滿足建模的基本要求,由于原序列具有季節性及漸升趨勢,故采用灰色季節趨勢法對模型進行擬合。最終模型通過后驗檢驗,對應的模型表達式為
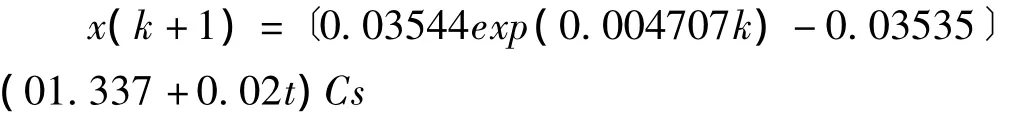
醫院感染序列實際值與預測值的MAPE值為19.03,對應的擬合圖形如圖4。
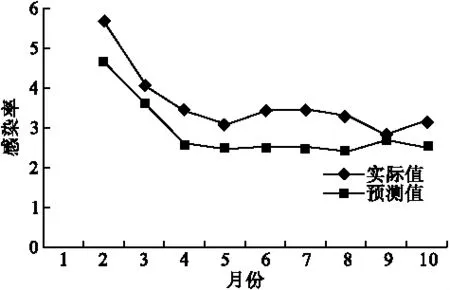
圖4 醫院感染率實際值與灰色模型預測值趨勢圖
5.模型評估
以2011年1~10月的醫院感染發生率資料作為模型評價樣本,對上述三種時間序列模型應用MAPE值判斷其預測精度,結果見表1。
三種時間序列模型的預測精度均為良好,其中指數平滑模型預測值與實際值間的MAPE值最小,為10.41,故指數平滑模型為該醫院感染發生率預測模型的最優模型。
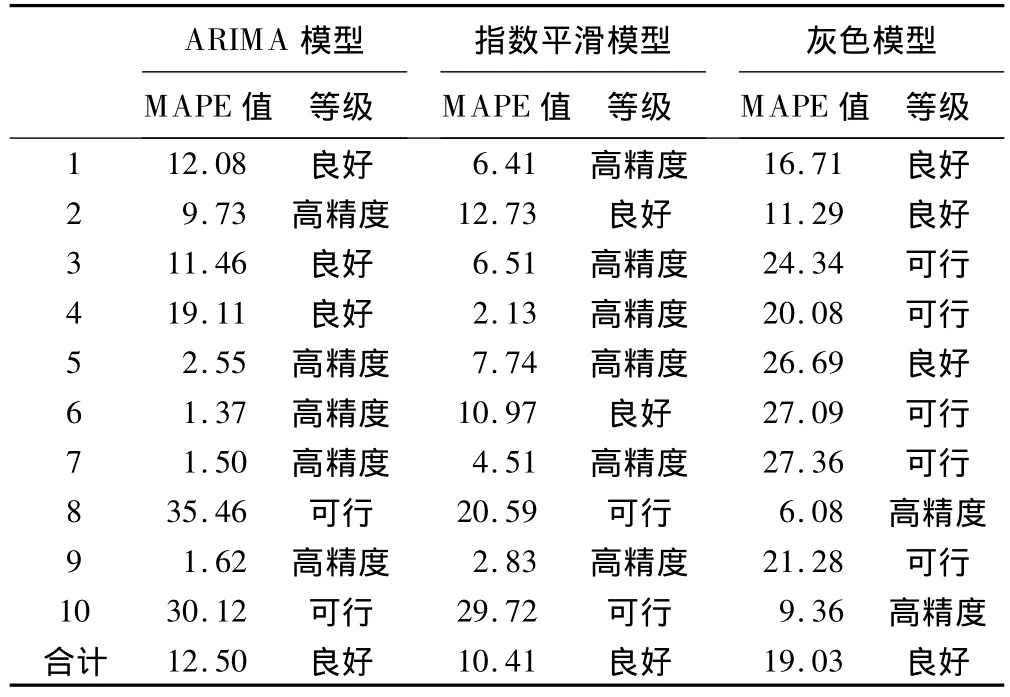
表1 不同月份各時間序列模型預測MAPE值及等級評價
討 論
統計預測是在大量統計資料的基礎上,運用數理統計方法研究事物發展變化趨勢和方向的預測方法。常用統計預測方法很多,諸如回歸分析法、時間序列法、灰色模型等等。有研究顯示,各種模型在疾病的預測中及醫院管理等方面均取得了較好的效果〔6-8〕。在國內外研究中,灰色模型、季節性時間序列的線性模型、人工神經網絡模型均已應用于醫院感染危險度的預測中,取得了良好的預期效果〔9-11〕。但醫院感染的發生受多種因素共同作用影響,在特定環境中,醫院感染發生率及其發展變化的趨勢不盡相同,在對特定醫院的醫院感染進行監控時,為提高監控效率,可應用統計預測技術進行院感的前瞻性研究,但哪種模型更適合該醫院的醫院感染危險度的預測,還需進一步探索。本文應用ARIMA模型、指數平滑模型、灰色模型對特定的醫院感染危險度進行構建,取得了預期效果,擬合值和實際值間預測的相對誤差絕對值平均在10~20之間,預測精度為良好,說明這三種對醫院感染率的預測具有可行性,其對醫院感染率的發生趨勢判斷具有參考價值。
ARIMA模型、指數平滑模型、灰色模型除其基本形式外,又都包括了多種衍生類型,各類型都有其不同適用條件,在模型擬合時一定要根據原序列的特征確定不同的模型類型才能得到較好的預測效果。本例資料由于有明確的季節性,故在各模型擬合時均選擇季節性類型。從三種模型擬合的趨勢圖看,灰色模型的預測值普遍小于其實際值,而ARIMA模型和指數平滑模型的預測值的擬合圖形軌跡與實際值較吻合,特別是指數平滑模型,其可能是由于ARIMA模型在操作過程中考慮到了序列的隨機性、平穩性和季節性,而指數平滑模型在考慮了整體均值、整體趨勢和季節性的同時又考慮的序列的最鄰近的值。醫院感染的發生雖有其明顯的季節性,但隨機性也較強,ARIMA模型和指數平滑模型都考慮了其隨機性,而灰色模型只能用于數據離散較小且發展趨勢呈單調性的情況,無法分析系統的波動規律〔12〕,即使在事先對數據進行了預處理,剔除了其趨勢性和季節性,但對序列隨機性的把握仍欠缺,且灰色模型在擬合時,由于其軟件只包含基本形式的預測用程序組,對其趨勢性和季節性均需先運算剔除后再回代,整個操作過程較前兩種模型復雜。
由于醫院感染的發生率資料收集相對較方便,故本次研究僅對醫院感染的發病率建立了一維的時間序列模型,在研究中發現其具有較強的可操作性和現實意義。但醫院感染的發生是諸多因素綜合影響的結果,可嘗試利用多元統計分析方法,將各影響因素的作用融入模型,借助先進工具進行分析預測,可能會使結果更加貼近實際,更具操作性。
1.王良俊,周霞,楊金霞,等.醫院感染監測中存在問題及對策.中華醫院感染學雜志,2008,18(4):492-493.
2.孫振球.醫學統計學.第2版 北京:人民衛生出版社,2005,7:461-462.
3.王燕.應用時間序列分析.第2版,北京:中國人民大學出版社,2008,12:149-150.
4.劉思峰,謝乃明,等.灰色系統理論及其應用.北京:科學出版社,2008.
5.劉思峰.預測方法與技術.北京:高等教育出版社,2005.
6.尹志英,繆明正.指數曲線模型在預測甲肝流行趨勢中的應用.中國衛生統計,2007,24(5):555.
8.胡興,胡錫健.新疆H1N1甲型流感預測模型的比較研究.中國衛生統計,2011,28(3):342-343.
7.肖玉霞,張穎.用線性趨勢季節模型預測出院人次.中國衛生統計,2008,25(3):213-215.
8.羅陽,丁國英,府偉靈,等.季節性時間序列分析在醫院感染中的應用.中華醫院感染學雜志,2005,15(4):390-392.
9.張素萍,王建斌,吳俊霞,等.醫院感染灰色模型監控效果的探討.中華醫院感染學雜志,2000,10(5):380-381.
11.許林勇,白毅,胡明,等.基于人工神經網絡模型的醫院感染危險度預測.中南大學學報,2006,31(3):404-407.
12.顏杰,相麗馳,方積乾.灰色預測模型及SAS實現.中國衛生統計,2006,23(1):75.

