基于剛架模型的多張B樣條曲面變形

李運平 周來水 王志國 陸友太

南京航空航天大學江蘇省精密與微細制造技術重點實驗室，南京，210016

0 引言

B－spline曲線曲面作為 STEP工業(yè)標準NURBS曲線曲面的特例(其權因子全為1)，是曲面造型領域中描述工業(yè)產(chǎn)品幾何外形的重要方法。由B－spline曲面的定義可知，通過改變節(jié)點矢量與控制頂點都可以實現(xiàn)曲面的變形［1-2］。然而，修改幾何參數(shù)的方式對于復雜形狀的曲面變形設計非常困難，且難以達到工程上的幾何光順性要求和設計精度。

為了避免這些缺陷，簡化設計過程，產(chǎn)生了基于物理的造型方法。Terzopoulos等［3］將基于能量模型的可變形曲線曲面造型技術引入到計算機圖形學中，模擬出旗幟在風中飄擺及地毯飄落等動態(tài)過程，為基于物理的變形技術奠定了基礎。近年來，基于物理的變形方法受到研究者的廣泛關注［4-5］。Celniker等［6］將有限元法引入到曲線曲面變形中，將曲面劃分為三角形板單元，在載荷作用與幾何約束下計算曲面變形。之后，基于有限元法的曲面變形技術得到了廣泛研究［7-10］。文獻［7-8］采用有限元法求解曲線曲面變形的思想，運用3次均勻B－spline描述變形曲線曲面，給出了相應的有限元網(wǎng)格模型，以控制頂點為求解未知量，建立總剛度矩陣方程，計算滿足約束的曲線曲面。成思源等［9］推導了 B－spline曲線曲面的可變形模型運動方程，并對其有限元求解方法進行了研究，用特征點作用下可變形B－spline曲線曲面的變形驗證了有限元法的有效性。采用有限元網(wǎng)格近似參數(shù)曲面會導致曲面自身的拓撲發(fā)生改變，因此，難以精確描述曲面間的光滑拼接關系。文獻［11］將初始幾何體整體或局部地嵌入到橫截面為圓形的梁結構中，通過施加載荷使梁結構產(chǎn)生形變，幾何體作為梁結構的一部分在載荷作用下隨梁結構一起產(chǎn)生變形。文獻［12］基于控制網(wǎng)格建立了剛架模型，實現(xiàn)了單張B－spline曲面形狀修改。文獻［11-12］避免了變形過程中曲面拓撲的改變，但是僅適用于單張B－spline曲面。

筆者借鑒剛架受力變形的思想，提出了一種剛架模型驅動多張B－spline曲面變形算法。通過“合并”曲面片的控制網(wǎng)格的手段創(chuàng)建剛架模型，將曲面變形問題轉化為剛架模型的變形。根據(jù)幾何約束、曲面片間光滑拼接條件和選取的優(yōu)化目標，計算曲面片控制頂點的變化，實現(xiàn)多張B－spline曲面片變形。

1 多張B－spline曲面剛架模型的創(chuàng)建

1.1 剛架模型

空間剛架模型是由梁單元相互連接而成的結構，用于驅動曲面變形，如圖1所示。梁單元的節(jié)點稱為剛架的節(jié)點，節(jié)點的自由度為6，根據(jù)自由度的不同，可將節(jié)點分為自由節(jié)點、固支節(jié)點與鉸支節(jié)點。

圖1 剛架模型

1.2 B-spline曲面的數(shù)學描述

B－spline曲面由2個方向的控制頂點網(wǎng)格、2個節(jié)點矢量和單變量B－spline基函數(shù)的乘積定義。假設給定由(m+1)×(n+1)個控制頂點Sij(i=0，1，…，m;j=0，1，…，n)構成的陣列組成一張控制網(wǎng)格，分別給定參數(shù)u(次數(shù)為k)與v(次數(shù)為l)和節(jié)點矢量U與V，就可以定義一張張量積為k×l次的B－spline曲面，其方程為

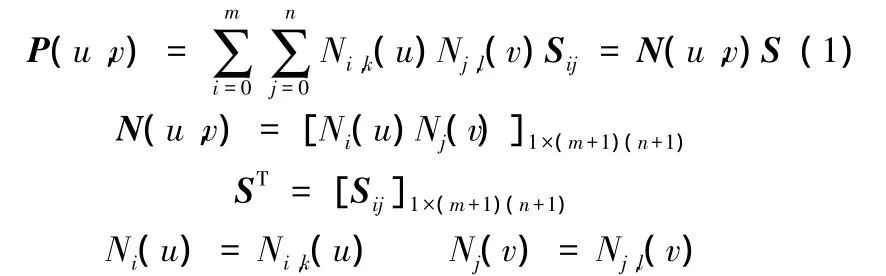
式中，Ni，k(u)是由節(jié)點矢量U定義的k次B－spline基函數(shù);Nj，l(v)是由節(jié)點矢量V定義的l次B－spline基函數(shù);N(u，v)為B－spline基函數(shù)乘積矢量;S為控制頂點矢量。

1.3 單張B-spline曲面的剛架模型

為了更好地反映控制頂點位置的改變對曲面形狀的影響，用曲面的控制頂點定義剛架模型的節(jié)點，依據(jù)控制網(wǎng)格的幾何拓撲關系生成相應的剛架模型。圖2所示為基于控制網(wǎng)格所創(chuàng)建的單張B－spline曲面的剛架模型，圓球為節(jié)點。

1.4 多張B-spline曲面的剛架模型

圖2 單張B-spline曲面的剛架模型

工業(yè)產(chǎn)品的幾何外形通常由4邊域B－spline曲面片拼接而成，且曲面片之間一般維持G1連續(xù)，即曲面片的每個公共頂點與位于兩側的各一個相鄰非公共頂點共線，如圖3所示，其中，P、P'為公共邊界處的重合點，P1、P2分別為兩側對應控制頂點。采取去掉重復控制頂點的方法合并控制網(wǎng)格，建立多張曲面的剛架模型，如圖4所示。圖4中，黑色球為固支節(jié)點，灰色球為自由節(jié)點。由圖4可知，剛架模型的節(jié)點和合并后的控制網(wǎng)格頂點是一一對應的，故節(jié)點的位移量等價于控制網(wǎng)格頂點的位移量。

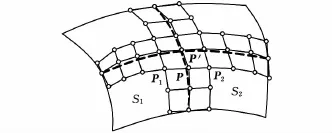
圖3 G1連續(xù)條件下多張B-spline曲面和控制網(wǎng)格

圖4 多張B-spline曲面剛架模型

2 多張B－spline曲面約束變形計算

2.1 基于有限元法的剛架模型節(jié)點位移計算

剛架模型在承受載荷的情況下，節(jié)點會產(chǎn)生相應的位移，根據(jù)線彈性有限元方法可知，載荷和節(jié)點位移滿足如下方程:

式中，K為整體剛度矩陣;Δ為節(jié)點位移列陣;P為節(jié)點載荷列陣。

在曲面造型過程中，為滿足工程的設計要求，將曲面設計要求抽象為幾何約束(點約束、點和法矢約束、等參線約束等)，在幾何約束下對曲面進行變形。根據(jù)多曲面剛架模型節(jié)點和控制網(wǎng)格頂點的一一對應關系，將曲面的約束變形問題轉化為剛架模型變形。以剛架模型節(jié)點位移為變量，構建了載荷最小與節(jié)點位移量最小的優(yōu)化目標，并建立統(tǒng)一的表達式，用于組合使用兩個最小化模型來滿足不同的變形要求。多曲面約束變形問題可描述為以剛架節(jié)點位移Δ為變量的函數(shù):

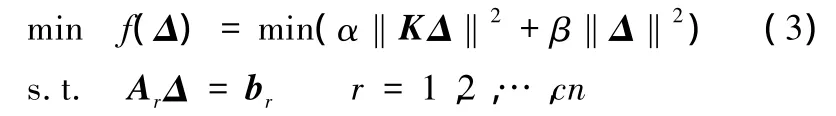
式中，‖KΔ‖2為節(jié)點載荷;‖Δ‖2為節(jié)點位移量;α、β為權因子，用于調整目標函數(shù)中每個優(yōu)化目標在變形中所占的比重;ArΔ=br為第r個約束的約束方程;Ar為約束方程的系數(shù)矩陣;br為列陣;cn為約束的個數(shù)。

由于優(yōu)化問題(式(3))中的目標函數(shù)為Δ的二次函數(shù)，約束方程為線性方程組，因此上述約束優(yōu)化問題為標準的等式二次規(guī)劃問題，可采用Lagrange乘子法和罰函數(shù)法進行求解。按照罰函數(shù)法將式(3)改寫成

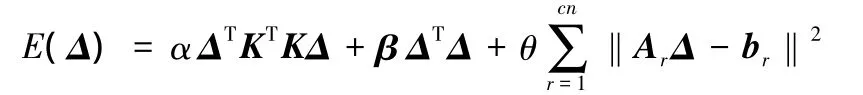
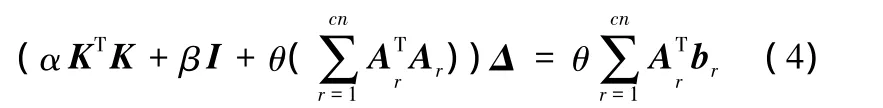
式中，I為單位矩陣。

由式(4)可以看出，罰函數(shù)法將約束優(yōu)化問題轉化為線性方程組的求解問題。本文先采用超松弛迭代預處理共軛梯度法(SSOR－PCG)求解節(jié)點位移Δ，然后根據(jù)節(jié)點和控制頂點的對應關系，計算曲面片控制頂點的新位置，完成多張曲面的約束變形。

由于總剛度矩陣K具有稀疏、對稱等特性，本文采用一維變帶寬壓縮存儲方法存儲矩陣，并選取SSOR－PCG迭代求解方程組。將式(4)簡記為FΔ=u，D為F的對角陣，L為F的嚴格下三角陣，求解方程組偽代碼如下:

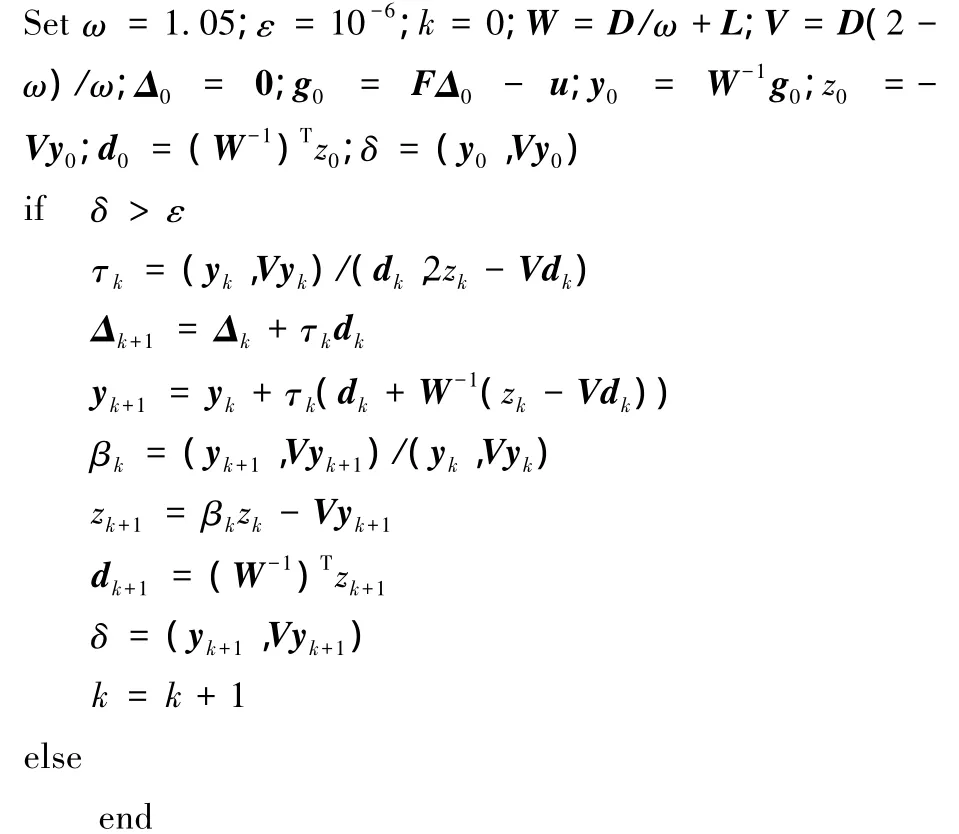
2.2 曲面片光滑拼接約束

為保證變形過程中曲面片之間的光滑拼接，將曲面片之間的光滑拼接關系作為約束條件。在圖3 中，曲面S1、S2為G1連續(xù)曲面，即P1、P、P2位于一條直線上，則?0≤t≤1，滿足:

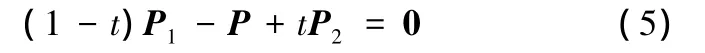
將式(5)改寫為以節(jié)點位移Δ為參數(shù)的線性方程組:

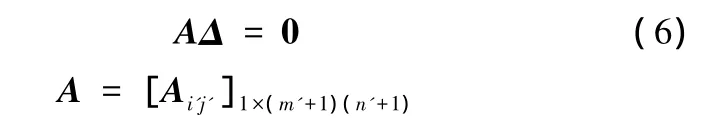
式中，Ai'j'(0≤ i'≤ m'，0≤ j'≤ n')為 3×6維矩陣，m'+1、n'+1分別為合并后的整合控制網(wǎng)格U、V向控制頂點數(shù)目。

記與 P1、P、P2對應的節(jié)點索引分別為 i'j'、k'l'、r's'(0≤k'≤m';0≤r'≤m';0≤l'≤n';0≤ s'≤ n')，則矩陣 A 除 Ai'j'、Ak'l'、Ar's'外，其余元素全為零矩陣。Ai'j'、Ak'l'、Ar's'分別為

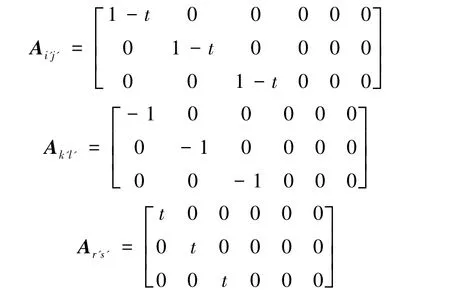
2.3 點約束變形

假定S0是曲面片Pw(u，v)=Nw(u，v)Sw上參數(shù)為(u0，v0)的點，T0為變形后曲面片P'w(u，v)上對應的目標點。 則變形后的曲面片 P'w(u，v)滿足:

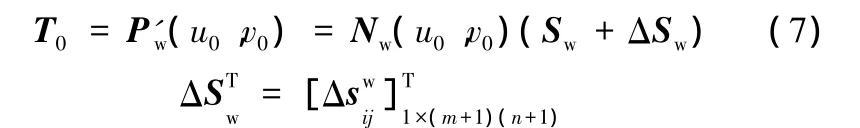
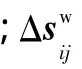
式(7)可以改寫為

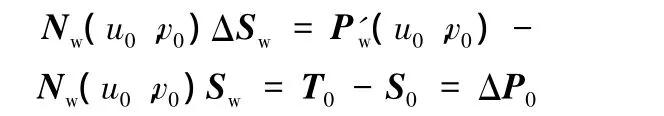
將上述方程轉化為以節(jié)點位移為變量的約束方程AΔ=b。其中，A的形式與式(6)中的系數(shù)矩陣一致，b= ΔP0=［Δx Δy Δz］T。

初始各曲面片的每一個控制頂點對應唯一的節(jié)點，元素Ai'j'取值主要有兩種情況:

(1)若控制頂點Swij和節(jié)點nodei'j'對應，記Nwij=Nwi(u)Nwj(v)，則元素Ai'j'可以表示為

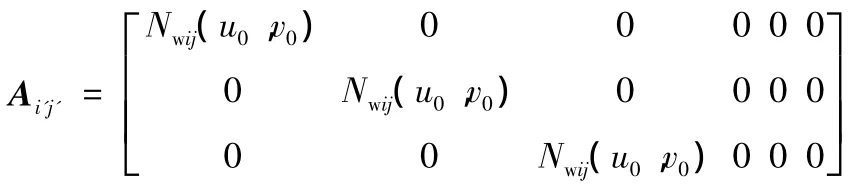
(2)若節(jié)點nodei'j'和任一控制頂點Swij未重合，則 Ai'j'=0。

在多點約束的情況下，點約束可能會分布在不同的曲面片上。通過上述討論分別計算將每個點約束轉化為約束矩陣ArΔ=br。

圖5所示為G1連續(xù)條件下4張B－spline曲面點約束變形結果。圖5a所示為G1連續(xù)條件下4張B－spline曲面及點約束，圖5b、圖5c所示分別為給定不同權因子的曲面變形結果。由圖5b、圖5c可以看出，變形后的曲面片都滿足給定的點約束條件，但隨著β的逐漸增大(節(jié)點位移最小優(yōu)化目標逐漸占較大比重)，曲面將逐漸由整體光順模型(圖5b)向局部尖銳模型(圖5c)過渡。因此，調節(jié)權因子可以獲得形狀各異的變形結果，為設計需求提供充足的素材。

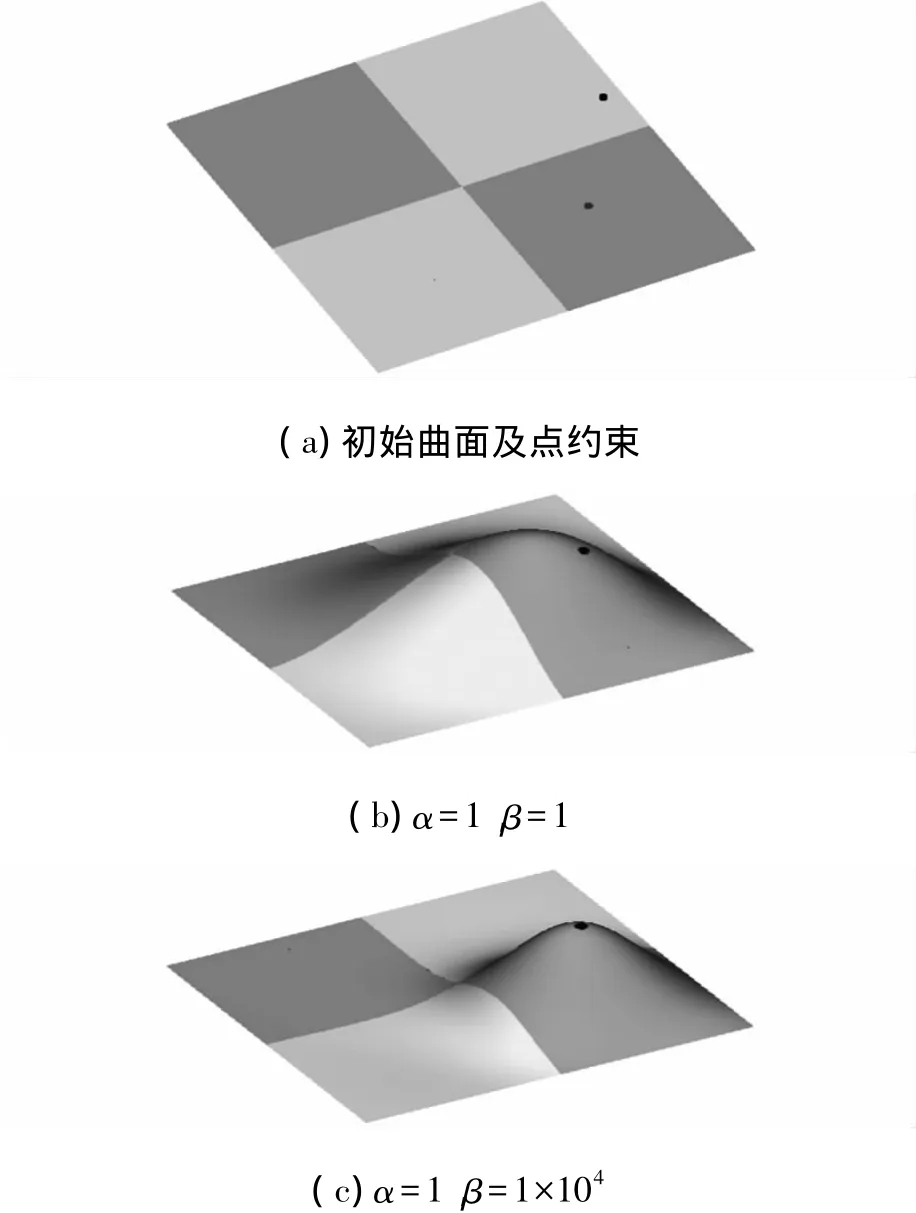
圖5 G1連續(xù)條件下4張B-spline曲面點約束變形

2.4 點與法矢約束變形

假設變形后的曲面片P'w(u，v)在參數(shù)點(u0，v0)處能精確通過點T0，且曲面在(u0，v0)處的法矢 n=(nx，ny，nz)，即曲面片 P'w(u，v)滿足:

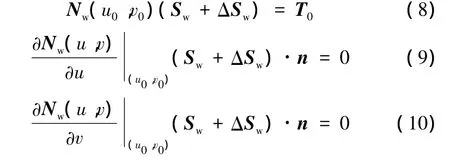
式(8)可以根據(jù)點約束下多張B－spline曲面變形中約束系數(shù)矩陣的求法轉換成AΔ=b的形式;式(9)、式(10)表達形式一致，其解決方法也類似。以式(9)為例，其約束方程式可以表示為

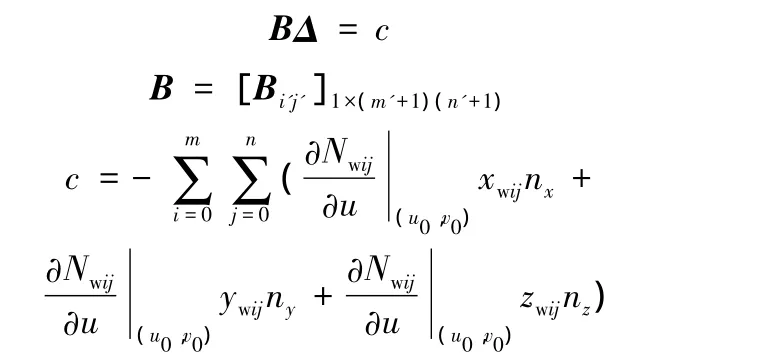
式中，Bi'j'為1×6維矩陣。

對約束矩陣元素 Bi'j'同樣需要進行分情況討論:

(1)若控制頂點Swij和節(jié)點nodei'j'對應，則元素Bi'j'為

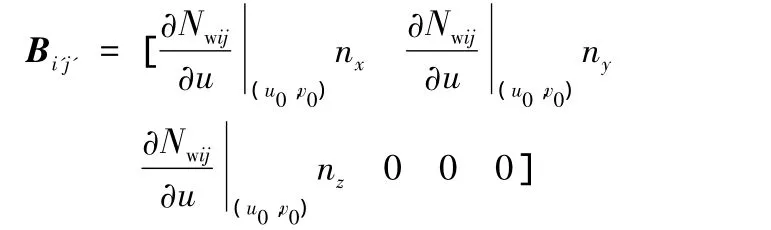
(2)若節(jié)點nodei'j'和任一控制頂點Swij未重合，則 Bi'j'=0。

同理，式(10)可以表示成CΔ=d的形式。

圖6所示為G1連續(xù)條件下基于點和法矢約束的3張B－spline曲面變形。圖6a所示為初始曲面及點與法矢約束，圖6b、圖6c所示為不同權因子值下B－spline曲面的變形效果。

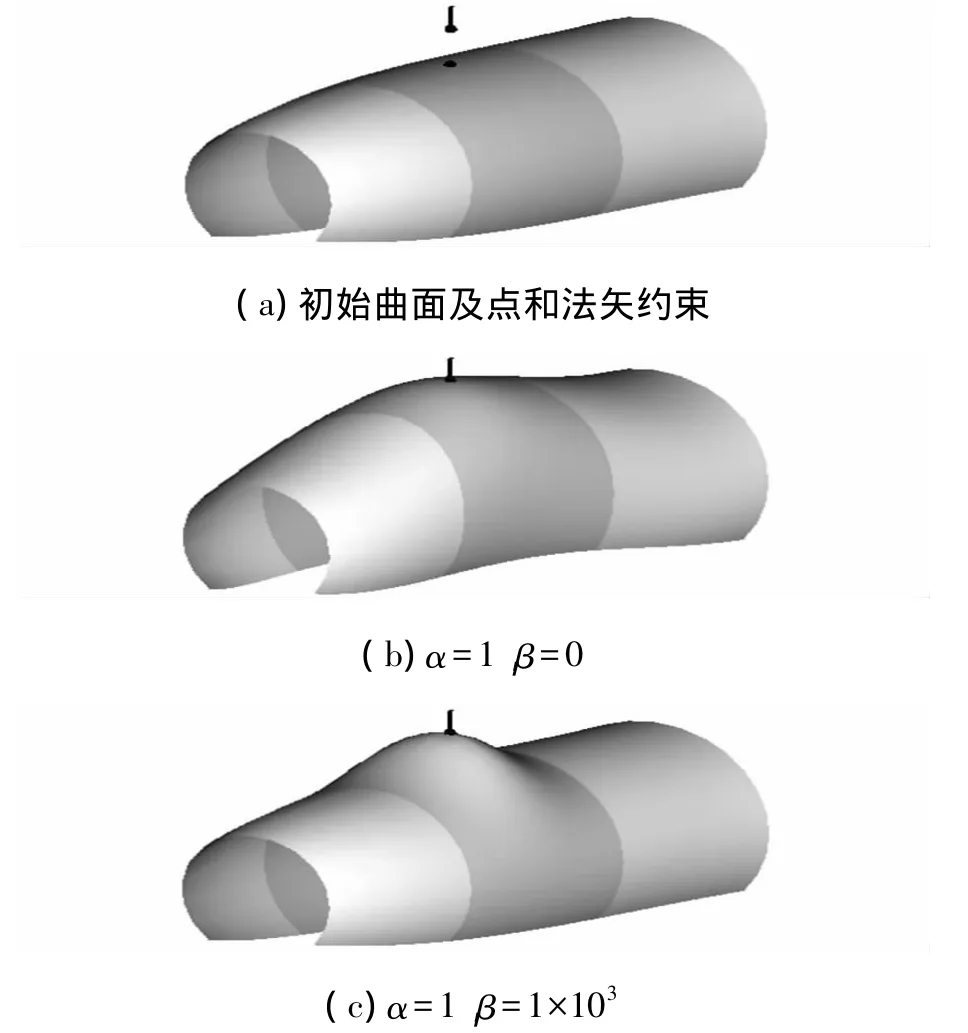
圖6 G1連續(xù)條件下3張B-spline曲面點與法矢約束變形

3 變形實例

基于剛架模型的多曲面變形方法已通過編程實現(xiàn)，實例中梁單元材料的彈性模量E=1kPa、泊松比μ=0.4，通過交互添加幾何約束使物體達到滿足特定需求的變形結果。圖7所示為自由曲面的點約束變形，圖7a中的自由曲面由3張B－spline曲面片通過G1拼接而成，黑色的點為初始曲面片上的點，黑色三角形為其相應的目標點，最終的變形結果如圖7b所示，實現(xiàn)了曲面精確變形到點約束位置的要求。

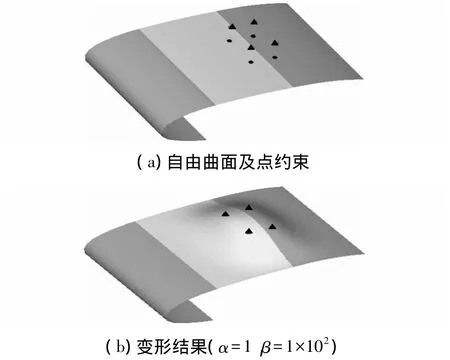
圖7 自由曲面點約束變形

和傳統(tǒng)的曲面變形方法相比，文中剛架模型的變形計算采用有限元的直接剛度法，由于總剛度矩陣是正定的，理論上一定可解。因此運用剛架變形原理進行復雜曲面的變形設計時，避免了拼接約束系統(tǒng)的可解性問題，本文方法可確保曲面片之間在變形過程中保持G1連續(xù)。表1所示為圖5～圖7曲面變形前后曲面片之間G1連續(xù)性條件分析數(shù)據(jù)，平均正弦為公共邊界點和兩側對應的控制頂點連線的矢量夾角正弦的平均值。由表1可以看出，變形前后的平均正弦值基本保持一致，即曲面片之間的光滑拼接狀態(tài)在變形中得到了有效的保持。

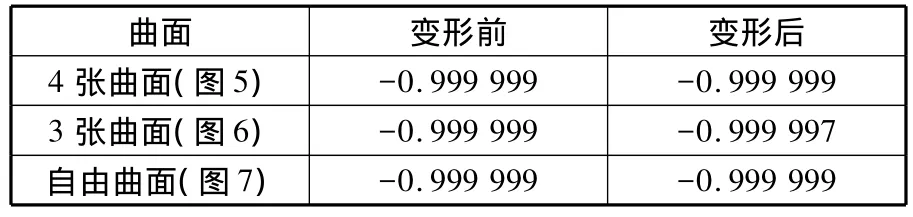
表1 多曲面變形前后G1連續(xù)性分析

運用本文算法計算多曲面變形時，要求每張曲面為4邊域B－spline曲面，且兩曲面片公共邊界處及兩側對應的控制頂點在一條直線上。在約束變形計算中，約束條件過多會導致剛架模型處于過約束狀態(tài)，進而無法生成滿足指定約束的變形結果。圖8所示為G1連續(xù)條件下基于點約束的2張B－spline曲面變形。其中，圖8a所示為初始曲面、曲面的剛架模型及點約束，圖8b所示為基于載荷最小模型的下B－spline曲面的變形結果。由圖8b可以看出，變形結果僅通過1個目標點。

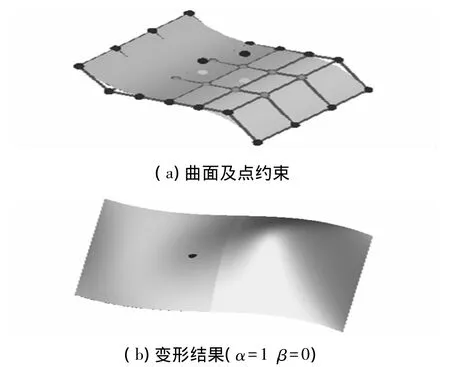
圖8 G1連續(xù)條件下2張B-spline曲面點約束變形

4 結語

結合剛架模型受力變形原理，提出了一種多張B－Spling曲面變形設計算法。給出了G1連續(xù)條件下多張B－spline曲面剛架模型的建立，以及曲面片之間光滑拼接條件的處理方法。算法實現(xiàn)了多張B－spline曲面在幾何約束下的變形協(xié)調設計，而且還能使曲面片之間保持變形前的光滑拼接狀態(tài)。

為增加變形算法的實用性可將本文方法擴展應用于NURBS表示的曲面變形設計;文中只提供了節(jié)點載荷最小和節(jié)點位移最小兩個優(yōu)化目標，后續(xù)工作可以進一步組合更多不同意義的優(yōu)化目標，以便達到理想的曲面變形效果。

［1］Piegl L.Modifying the Shape of Rational B－splines.Part 1:Surfaces［J］.Computer－Aided Design，1989，21(9):538-546.

［2］李亞娟，汪國昭.改變B樣條曲面與NURBS曲面的節(jié)點［J］.計算機輔助設計與圖形學學報，2005，17(5):986-989.Li Yajun，Wang Guozhao.On Knot Modifications of B－spline or NURBS Surface［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2005，17(5):986-989.

［3］Terzopoulos D，Platt J，Barr A.Elastically Deformable Models［J］.Computer Graphics，1987，21(4):205-214.

［4］Wang Z G，Zhou L S，Wang X P.Direct Manipulation of B－spline Surfaces［J］.Chinese Journal of Mechanical Engineering，2005，18(1):103-108.

［5］王青，柯映林，李江雄.基于力密度方法的NURBS曲線和曲面變形框架［J］.機械工程學報，2007，43(3):135-142.Wang Qing，Ke Yinglin，Li Jiangxiong.Shape Modification of NURBS Curves and Surfaces Based on Force Density Method［J］.Journal of Mechanical Engineering，2007，43(3):135-142.

［6］Celniker G，Gossard D.Deformable Curve and Surface Finite Elments for Free－form Shape Design［J］.Computer Graphics，1991，25(4):257-266.

［7］Guan Z D，Jing L，Ning T，et al.Study and Application of Physics－based Deformable Curves and Surfaces［J］.Computers ＆ Graphics，1997，21(3):305-313.

［8］成思源，張湘?zhèn)?可變形B樣條曲線曲面模型及其有限元求解［J］.重慶大學學報，2003，26(2):75-77.Cheng Siyuan，Zhang Xiangwei.Deformable B－spline Curves and Surfaces Model and Its Finite Element Solution［J］.Chinese Journal of Chongqing University，2003，26(2):75-77.

［9］經(jīng)玲，席平，唐榮錫.有限元方法在變形曲線曲面造型中的應用［J］.計算機學報，1998，21(3):245-251.Jing Ling，Xi Ping，Tang Rrongxi.Application of Finite Element Method in Deformable Curve and Surface［J］.Journal of Computers，1998，21(3):245-251.

［10］程仙國，劉偉軍，卞宏友.基于外載荷的B樣條曲面變形［J］.機械工程學報，2011，47(9):146-150.Cheng Xianguo，Liu Wweijun，Bian Hongyou.Shape Modification of B－spline Surface via External Loads［J］.Journal of Mechanical Engineering，2011，47(9):146-150.

［11］Wang Z G，Wang X P，Bao Y D，et al.Shape Modification by Beam Model in FEM［J］.Chinese Journal of Aeronautics，2010，23(2):246-251.

［12］Yu C S，Zhou L S，Wang Z G，et al.Shape Modification of B－spline Surfaces Based on Rigid Frame via Geometric Constraint Optimization［C］//Proceedings of the Conference on Intelligent Human－machine Systems and Cybernetices.Hangzhou，2011:120-124.