成敗型產品可靠性評價的加權Bayes方法

劉解放 劉思峰 方志耕

1.南京航空航天大學，南京，210016 2.河南科技學院，新鄉，453003

0 引言

產品可靠性評價通常以產品的可靠性試驗為依據。一般來說，試驗的次數越多，得到的可靠性評價的置信度越高，因此，為了在較大的置信度下評價產品的可靠性，往往需要做大量的試驗。許多試驗通常對產品具有破壞性，尤其對于一些造價昂貴、危險性高的產品，往往會造成試驗費用的大量增加，導致試驗費用在研發中的比例過高。Bayes方法能夠利用歷史信息，從而有效減少現場試驗的次數，近年來得到了廣泛的應用［1-3］。

運用Bayes方法進行可靠性評價，首先要根據先驗信息確定先驗分布，對于成敗型試驗總體，先驗分布往往是取其共軛Beta分布，其密度函數為［4-5］

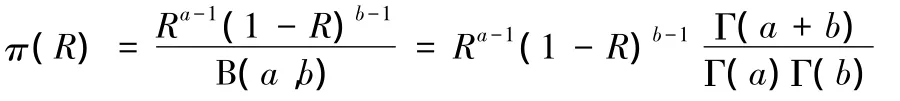
式中，R 為可靠度;a、b為驗前超參數;Γ()為 Gamma函數。

驗前超參數的確定主要依靠驗前試驗信息，目前已經有很多方法來求解驗前超參數，文獻［6］對這些方法進行了總結。

1 傳統的Bayes可靠性評估方法

確定了先驗分布的超參數(a，b)后，若錄得現場試驗數據(n，f)，其中n為成功數，f為失敗數，則可以得到后驗分布為B(R|a+n－f，b+f)，其密度函數為

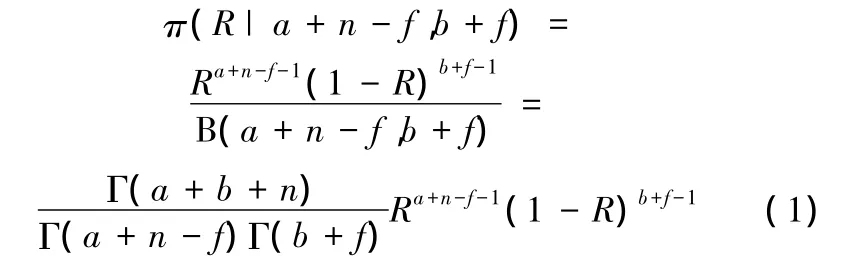
給定置信度γ，則系統的可靠性下限RL可由下式求出:

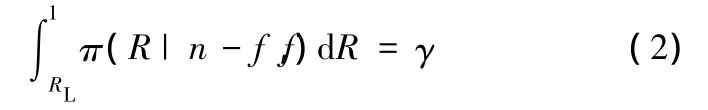
上述傳統Bayes方法假設歷史試驗樣本和現場試驗樣本來自同一個總體，對歷史數據和現場數據不加區別。事實上，對于具有多研制階段的產品，根據上一階段的試驗結果，產品的性能在不斷調試，把各階段的試驗數據和現場的試驗數據視為來自同一總體是不妥的。特別是當歷史數據較多、現場數據較少時，有可能使評估結論產生較大偏差。以可靠性的點估計為例，可靠性的驗后點估計為

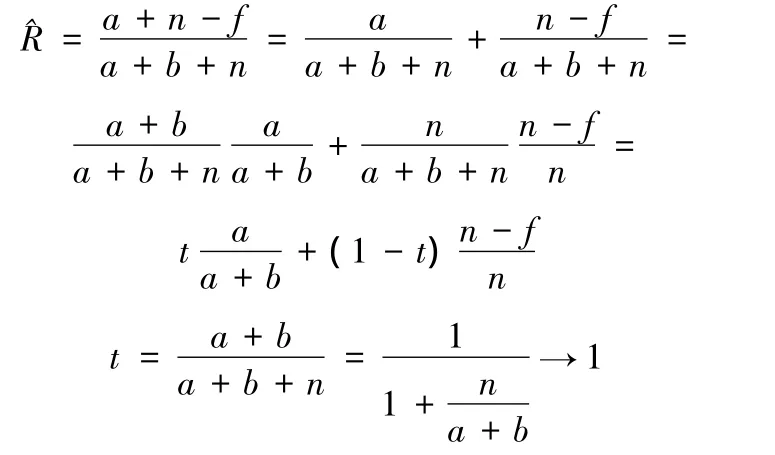
則

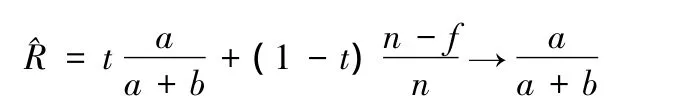
即驗后可靠性的點估計趨于可靠性的驗前點估計，就會出現歷史信息淹沒現場試驗信息的現象，使得現場試驗信息的作用變得極為有限。為了合理地使用歷史試驗樣本，需要對驗前試驗信息與現場試驗信息是否來自同一樣本進行檢驗。

2 相似系數的確定

設歷史信息綜合后的試驗樣本(S，F)來自總體Y，現場試驗樣本(n－f，f)來自總體X，可以排成如表1所示的列聯表［7］。

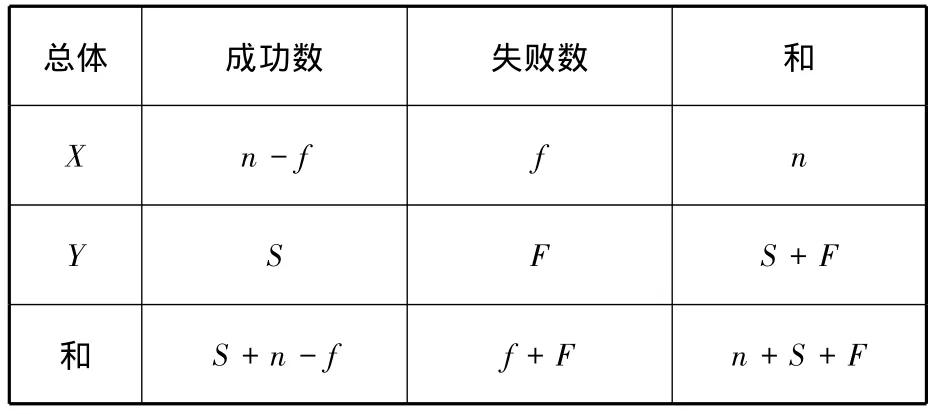
表1 現場總體X和混合總體Y的列聯表

令

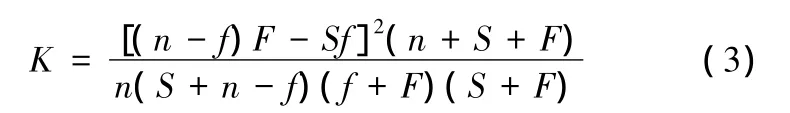
其中，K為Person統計量，依分布收斂到自由度為1的χ2分布。但是在使用式(3)時，要求n－f、f、S、F均大于5。對于小樣本的情況，試驗數量往往較少，不能滿足這個條件，文獻［8］對其進行如下修正:

因為K近似服從自由度為1的χ2分布，因此在給定檢驗水平α的情況下，可以將K作為檢驗統計量，對X和Y兩個總體是否為同一總體這個假設進行檢驗，若通過了相容性檢驗，即可確定歷史信息與現場信息的相似程度的大小ρ。

設

為上述檢驗的擬合優度，Q依概率的形式表征出X和Y兩個總體的相似程度，與ρ有直接的關系［9］，可取

設階段i的試驗樣本(ai，bi)來自總體Yi，現場試驗樣本(n－f，f)來自總體X，可以排成與表1類似的聯表。

此時，取

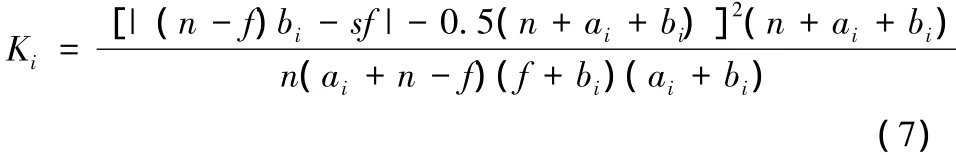
然后計算

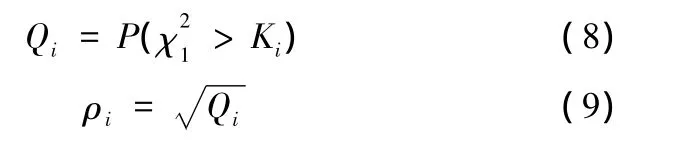
3 多階段試驗信息的融合

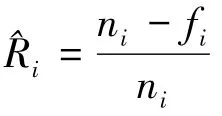
(1)當試驗的批次較多，即m較大時，有

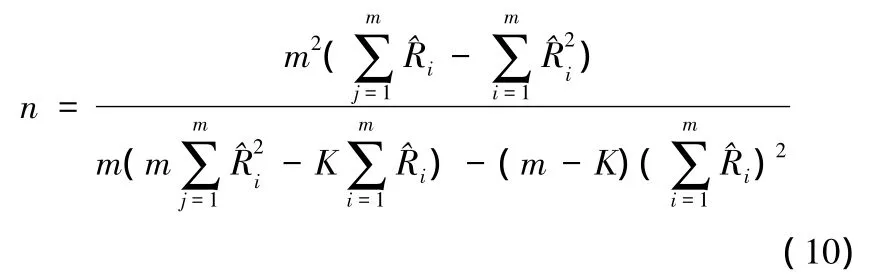
進而求得

(2)當試驗的批次較少，即m較小時，抽樣誤差可能使得式(10)為負值，此時可作以下修正:

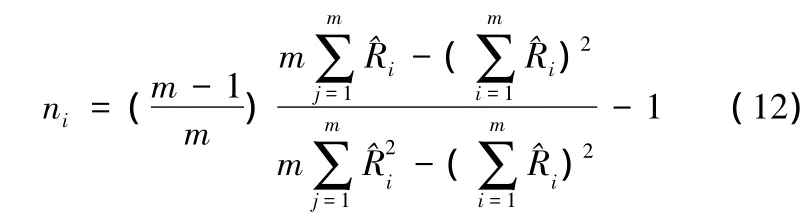
根據式(4)求出(S，F)與現場試驗數據(nf，f)的相似度ρ，同理，求出每一階段的成功數和失敗數(ai，bi)和現場試驗數據(n－f，f)的相似度 ρi，然后利用下式

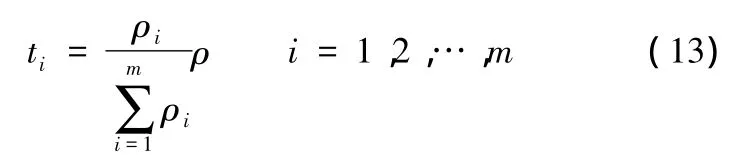
確定各階段的系數可靠性ti。

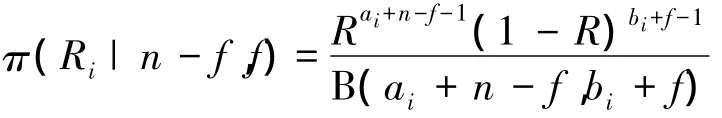
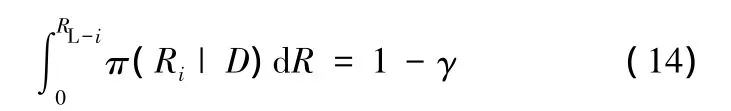
建立如下形式的成敗型產品可靠性評價的加權Bayes方法:

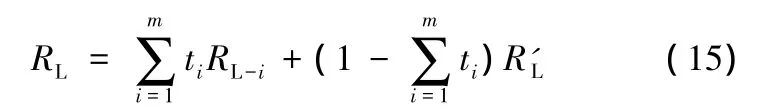
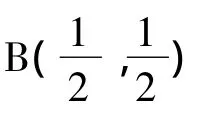
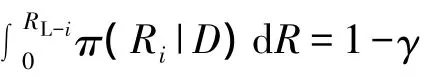
4 仿真數據分析

某產品研制信息分為5個階段，以往的試驗信息見表2。

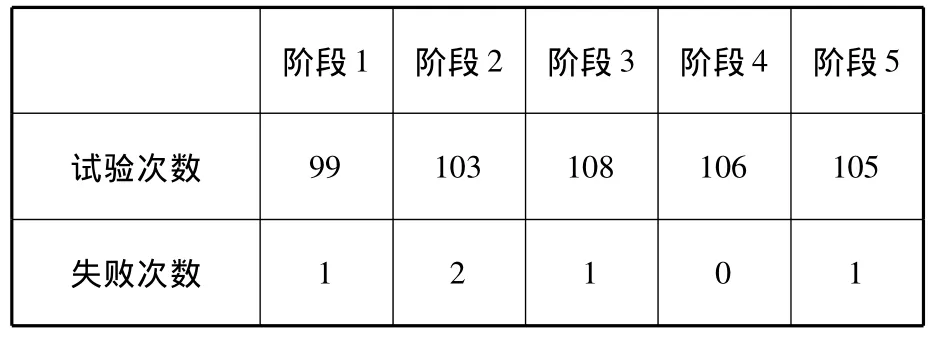
表2 歷史試驗數據統計

根據現場試驗錄得以下數據:n=22，f=1。

(1)若采用經典統計的方法，只考慮現場試驗的信息，則根據文獻［6］，有

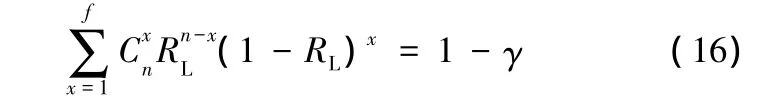
其中，γ為置信水平，RL為在置信水平γ下的置信下限，取γ=0.1，求得置信下限RL=0.8344，由于經典統計方法只利用了少量現場試驗信息，評價結果顯得過于保守，不符合產品定型的要求。

(2)傳統Bayes方法。先根據經驗Bayes方法對歷史信息進行融合，根據式(12)求得S=199.6384，F=1.9474，即驗前信息分布折合為B(199.6384，1.9474)。若把歷史信息與現場信息視為來自同一樣本，直接進行融合，即取驗后分布為 B(199.6384+s，1.9474+f)，其中 s=21，f=1。 取置信水平 γ=0.1，求得置信下限RL=0.9766。由于歷史試驗樣本的數量遠大于現場試驗樣本的數量，評價結果嚴重依賴歷史信息，出現了歷史信息淹沒現場試驗信息的現象，評價結果比較冒進，風險較大。

(3)采用本文提出的方法進行計算。首先根據經驗 Bayes方法，求得 S=199.6384，F=1.9474。然后根據式(4)～式(6)求得K=0.1709，Q=0.6793，進而求得 ρ=0.8242。按照同樣步驟，對研制階段的信息與現場信息進行擬合優度檢驗，分別求得的結果如表3所示。

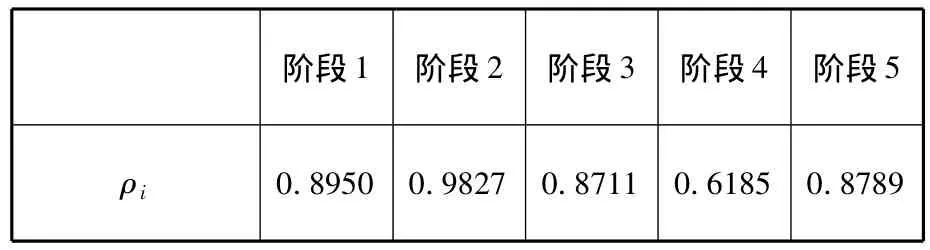
表3 不同試驗階段與現場試驗的相似系數

根據式(7)求得權重為 t1=0.1737，t2=0.1907，t3=0.1691，t4=0.1201，t5=0.1706。利用Bayes公式計算第i階段試驗信息的可靠性置信下限RL－i，如表4所示，此處取置信度γ =0.9。

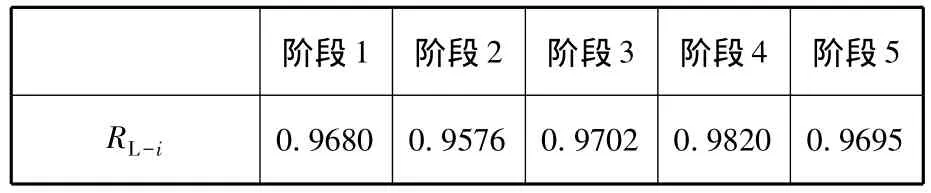
表4 第i階段試驗信息的可靠性置信下限(γ=0.9)

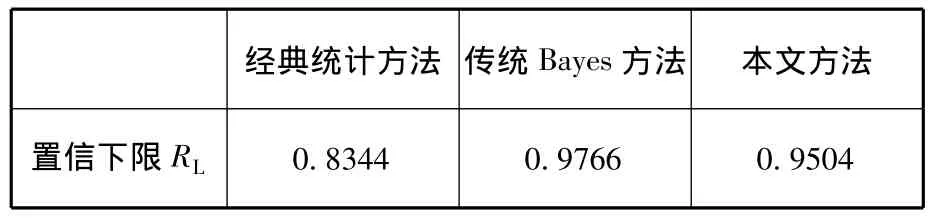
表5 不同方法下的可靠性置信下限(γ=0.9)

由表5可看出，經典統計方法只利用現場試驗信息，結果偏保守;傳統Bayes方法把現場試驗信息和歷史信息視為來自同一總體的樣本，計算結果偏冒進，加大了評價的風險;采用本文提出的方法，由于考慮了現場試驗信息和歷史信息異總體性，評價結果更為合理。根據工程領域專家的意見，折合后歷史試驗信息B(199.6384，1.9474)的權重ρ'1=0.8，現場試驗信息的權重ρ'2=0.2，計算得到產品可靠性的置信下限為R2L=0.9518，與本文的計算結果最接近。相對于傳統的Bayes方法，利用本文方法得到的評價結果風險明顯減小。

5 結語

對具有多階段信息的產品，其各個階段的試驗樣本與現場的試驗樣本具有異總體性，為了測度它們之間的關系，引入了相似系數的概念，通過卡方擬合優度檢驗，確定各個階段的試驗樣本與現場的試驗樣本的相似系數，并把整體驗前折合信息與現場實驗信息的相似系數向各個階段分配，從而計算得到融合各階段試驗信息的產品可靠性置信下限，與經典統計方法和傳統Bayes方法相比，得到的結果更加合理。

［1］宋保維，嚴衛生，徐德民.魚雷可靠性評定中的Bayes方法［J］.機械科學與技術，1998，17(3):371-374.Song Baowei，Yan Weisheng，Xu Demin.Bayes Method for Torpedo Reliability Assessment［J］.Mechanical Science and Technology，1998，17(3):371-374.

［2］常春賀，曹鵬舉，楊江平，等.基于研制階段試驗數據的復雜裝備測試性評估［J］.中國機械工程，2012，23(13):1577-1581.Chang Chunhe，Cao Pengju，Yang Jiangping，et al.Testability Evaluation of Complex Equipment Based on Test Data in Development Stages［J］.China Mechanical Engineering，2012，23(13):1577-1581.

［3］游達章，唐小琦，戴怡，等.貝葉斯理論的可靠性評估方法及在數控系統評估中的運用［J］.中國機械工程，2011，22(3):314-317.You Dazhang，Tang Xiaoqi，Dai Yi，et al.Reliability Estimation of CNC System Based on Bayes Method［J］.China MechanicalEngineering，2011，22(3):314-317.

［4］茆詩松.貝葉斯統計［M］.北京:中國統計出版社，1999.

［5］周源泉.可靠性評定［M］.北京:科學出版社，1990.

［6］張金槐.Bayes試驗分析中驗前分布的表示［J］.國防科技大學學報，1999，21(6):109-113.Zhang Jinhuai.Bayes Test Analysis for the Prior Distribution of Representation［J］.Journal of National University of Defense Technology，1999，21(6):109-113.

［7］艾沃日特 B S.列聯表分析［M］.劉韻源，周家麗，譯.北京:科學出版社，1980.

［8］劉晗，郭波.研制階段的成敗型產品可靠性Bayes評估［J］.可靠性與環境適應性理論，2006，24(5):25-29.Liu Han，Guo Bo.Bayes Assessment for Reliability of Success or Failure Product in the Development Phases［J］.Electronic Product Reliability and Environmental Testing，2006，24(5):25-29.

［9］王瑋，周海云，尹國舉.使用混合Beta分布的Bayes方法［J］.系統工程理論與實踐，2005，25(9):142-144.Wang Wei，Zhou Haiyun，Yin Guoju.Bayes Method with Mixed Beta Distribution［J］.Systems Engineering Theory ＆ Practice，2005，25(9):142-144.

［10］Martz H F，Waller R A.The Basics of Bayesian Reliability Estimation from Attribute Test Data［R］.New Mexico:Los Alamos Scientific Laboratory，1976.